117 Лекция 5 лекция 5
Анализ точности оценки коэффициентов регрессии. Стандартные ошибки регрессии и коэффициентов регрессии. Проверка гипотез относительно коэффициентов регрессии. Интервальные оценки коэффициентов регрессии. Показатели качества уравнения регрессии. Коэффициент детерминации. Критерий Фишера. Интервалы прогноза по уравнению регрессии.
Анализ точности оценок коэффициентов регрессии
Оценка дисперсии случайного отклонения 2
Проведем статистический анализ построенного уравнения регрессии, т.е. выясним насколько надёжны полученные оценки коэффициентов регрессии; как хорошо полученное уравнение регрессии описываем имеющиеся статистические данные, может быть следует изменить спецификацию модели; оценить точность прогноза, т.е. построить доверительный интервал для зависимой переменной. Для того чтобы провести такой статистический анализ модели, нужно, как мы видели в предыдущей лекции, знать закон распределения случайной величины . При построении уравнения регрессии МНК такой информации не требовалось (в этом одно из преимуществ МНК), однако для проведения статистического анализа такая информация востребована. В дальнейшем мы будем работать в рамках нормальной классической регрессионной модели, т.е. выполняются все условия Гаусса-Маркова и, в частности, подчиняется нормальному закону распределения. Вообще говоря, выполнимость этих условий ещё надо проверить, в данной лекции мы будем предполагать, что эти условия априори выполняются.
Сформулированные выше статистические свойства МНК-оценок коэффициентов регрессии справедливы и без предположения о нормальности случайного отклонения . Однако, даже располагая информацией о состоятельности, несмещённости и оптимальности оценок, мы не можем решить задачи о построении доверительных интервалов для истинных значений рассматриваемых параметров, так же как и для неизвестных значений функции регрессии. Необходимой базой для решения этих задач является знание законов распределения вероятностей используемых оценок. Именно в рамках нормальной классической линейной регрессионной модели можно решить вопросы о значимости коэффициентов регрессии и построении для них доверительных интервалов, о качестве построенного уравнения регрессии в целом, о точности прогноза по этому уравнению.
В
силу того, что случайные отклонения i
по выборке определены быть не могут,
при анализе надежности оценок коэффициентов
регрессии они заменяются отклонениями
значений yi
переменной Y
от оцененной линии регрессии. Не следует
путать эмпирические отклонения ei
с теоретическими отклонениями i.
И те и другие являются случайными
величинами, однако разница состоит в
том, что эмпирические отклонения, в
отличие от теоретических, наблюдаемы.
Кажется
вполне естественной гипотеза, что оценка
2
связана с суммой квадратов остатков
регрессии
.
В самом деле,
,
где
,
.
Тогда
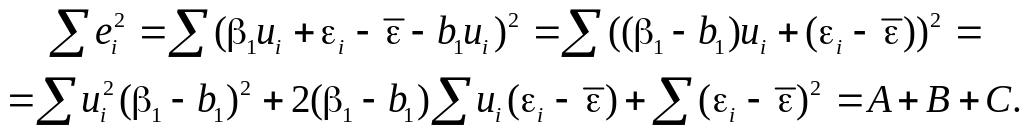
Вычислим
математическое ожидание
.
.
Используя
соотношение
,
получаем
,
.
Таким образом,
.
Отсюда следует, что
.
(5.34)
является несмещенной оценкой дисперсии случайного отклонения 2. Отметим, что S называется стандартной ошибкой регрессии,
Отметим, что в математической статистике для получения несмещенной оценки дисперсии случайной величины соответствующую сумму квадратов отклонений от средней делят не на число наблюдений n, на число степеней свободы n–m, равное разности между числом независимых наблюдений случайной величины n и числом связей, ограничивающих свободу их измерения, т.е. число m уравнений, связывающих эти наблюдения. Поэтому в знаменателе выражения (5.34) стоит число степеней свободы n–2, т.к. две степени свободы теряются при определении двух параметров прямой из системы нормальных уравнений.