Лабораторная работа № 6 разработка системы управления на основе нейросетевого регулятора

Цель работы. Ознакомление с демонстрационным примером по идентификации и синтезу нейросетевой модели регулятора NARMA-L2 и разработка системы управления объектом с двумя накопителями энергии.

Домашнее задание

1. Укажите свойства и основные закономерности, присущие сложным системам. В чем заключается смысл понятия «система»?

2. Опишите основные этапы проектирования регулятора NARMA-L2.

3. Ознакомиться с набором визуальных объектов библиотеки Simulink, которые можно использовать для исследования сложных динамических систем, а также с примером построения динамической модели управляемого процесса по перемещению магнита в электромагнитном поле.

Краткие сведения из теории

Многослойные нейронные сети успешно применяются для решения задач управления динамическими процессами, происходящими в сложных системах. На их основе осуществляется проектирование различных по принципу действия нелинейных регуляторов, использующихся для обучения и эффективного управления сложными системами.

Примерами регуляторов для управления сложными системами являются:

• регулятор с предсказанием;

• регулятор на основе модели авторегрессии со скользящим средним;

• регулятор на основе эталонной модели.

Задача проектирования регуляторов состоит из двух этапов: идентификации управляемого процесса и синтеза закона управления.

На этапе идентификации разрабатывается модель управляемого процесса в виде нейронной сети, которая на следующем этапе проектирования используется для синтеза регулятора.

Для различных архитектур многослойной нейронной сети применяется одна и та же процедура идентификации, однако этапы синтеза закона управления существенно различаются.

При управлении с предсказанием модель управляемого процесса используется для того, чтобы предсказывать его будущее поведение, а алгоритм оптимизации применяется для расчета такого управления, которое минимизирует разность между желаемыми и действительными изменениями выхода модели.

При управлении на основе модели авторегрессии со скользящим средним регулятор представляет собой достаточно простую реконструкцию модели управляемого процесса.

При управлении на основе эталонной модели регулятор отслеживает поведение эталонного процесса, причем модель управляемого процесса активно используется для настройки параметров самого регулятора.

Рассмотрим этапы проектирования нелинейного регулятора NARMA-L2 на демонстрационном примере управления магнитной подушкой, реализованного в ППП Neural Network Toolbox.

Наиболее просто выполнить запуск демонстрационного примера можно вводом команды narmamaglev в командном окне системы MATLAB. При этом открывается окно системы Simulink со следующей структурой системы управления (рис. 1).

Рис.1.

В систему управления магнитной подушкой входят:

• блок управляемого процесса Plant;

• блок контроллера NARMA-L2 Controller;

• блок генерации эталонного ступенчатого сигнала со случайной амплитудой Random Reference;

• блок отсчета времени Clock;

• блок построения графиков Graph.

Особенность данной структуры заключается в том, что она выполняет не только функции блок – схемы системы Simulink, но и функции графического интерфейса пользователя GUI.

В демонстрационном примере управляемым объектом является постоянный магнит, который движется только в вертикальном направлении в магнитном поле, как это показано схематично на рис. 2.

Рис. 2.

Уравнение движения постоянного магнита имеет вид:

где y(t) - перемещение магнита, отсчитываемое от электромагнита; g - ускорение силы тяжести; α - постоянная, зависящая от числа витков обмотки и намагниченности стального сердечника; i(t) - управляющий ток в обмотке электромагнита; М – масса постоянного магнита.

Динамическая модель управляемого процесса, соответствующая уравнению движения постоянного магнита, но с конкретными числовыми данными приведена на рис. 3.

Рис. 3.

Эту модель можно увидеть на экране монитора, если активизировать блок Plant (Magnet Levitation) в окне Model Browser. Рассматриваемая динамическая модель является нелинейной, поэтому в качестве модели управляемого процесса используем ее дискретную нелинейную модель как авторегрессионную модель со скользящим средним или NARMA- модель в форме

где y(k) - выход модели; d - число тактов предсказания; u(k) - вход модели.

Для практического решения задачи слежения используем приближенную NARMA-модель с выделенной составляющей управления. Такая модель регулятора, именуемая моделью NARMA-L2, имеет вид:

y(k+d) = f[y(k),y(k-1),…,y(k-n+1),u(k-1),…,u(k-m+1)] +

+ g[y(k),y(k-1),…,y(k-n+1),u(k-1),…,u(k-m+1)]u(k)

Преимущество этой формы состоит в том, что можно непосредственно вычислить текущее управление, если известна желаемая траектория y_r, предыстория управ­ления [u(k-1),…,u(k-m+1)], а также предшествующие и текущее значения выхода [y(k),y(k-1),…,y(k-n+1)]:

Однако непосредственное применение этого соотношения для реализации регулятора оказывается затруд­нительным, так как управление u(k) зависит от текущего значения выхода y(k). Поэтому модифицируем его следующим образом:

Параметр предсказания при этом должен удовлетворять условию d ≥ 2.

На рис. 4 показана укрупненная структура соответствующего регулятора NARMA-L2 в виде двухслойной нейронной сети. Здесь следует обратить внимание на участки нейронной сети, которые выполняют аппроксима­цию нелинейных операторов g и f в виде выходов и . Входами регуля­тора являются сигналыy(t+1) и u(t+1), последний реализован в виде обратной связи, а также эталонный сигнал y_r(t+2). Блоки задержки (ЛЗ) осуществляют запоминание соответст­вующих последовательностей входа и выхода, а затем используются двухслойные ней­ронные сети, которые формируют оценки нелинейных операторов и вычисляют сигнал управления в соответствии с приведенной выше формулой.

Рис. 4.

Общая структурная схема системы с регулятором NARMA - L2 приведена рис. 5. На схеме явным образом выделена эталонная модель, которая задает перемещение постоянного магнита в магнитном поле по желаемой траектории.

Рис. 5.

Демонстрационный пример NARMA - L2 Controller использует следующие файлы, размещенные в каталоге toolbox\nnet\nncontrol.

МАТ - файлы данных: ball1 – данные для обучения нейросетевой модели магнитной подушки;

Функции активации в нейронной сети регулятора NARMA- L2:

netinv – функция активации; dnetinv - производная функции активации;

Модели Simulink:

ballrepel0 – модель магнитной подушки; narmamaglev – GUI – приложение для контроллера NARMA- L2;

Вспомогательные функции: sfunxy2-S – функция для вывода графиков; nncontrolutil – утилита, обеспечивающая возможность обращения к частным функциям из системы Simulink.

Для начала работы необходимо активизировать блок NARMA-L2 - Controller двойным щелчком левой кнопки мыши в окне системы Simulink. Появится окно Plant Identification – NARMA - L2 (рис. 6).

Рис. 6.

Оно выполняет функции графического интерфейса пользователя и руководит его действиями в виде сообщения, указанного в области фрейма: «Прежде чем установить параметры контроллера, постройте модель управляемого процесса», то есть необходимо построить нейросетевую модель.

Процедура идентификации требует задания следующих параметров:

• Size of Hidden Lauer - размер скрытого слоя определяется количеством используемых нейронов;

• Sampling Interval - такт дискретности в секундах между двумя последовательными моментами съема данных;

• No. Delayed Plant Inputs – количество элементов запаздывания на входе модели;

• No. Delayed Plant Outputs - количество элементов запаздывания на выходе модели;

• Normalize Training Data – окно контроля нормирования обучающих данных к диапазону [0 1];

• Параметры обучающей последовательности:

• Training Samples – длина обучающей выборки (количество точек съема информации);

• Maximum Plant Input - максимальное значение входного сигнала;

• Minimum Plant Input - минимальное значение входного сигнала;

• Maximum Interval Value (sec) - максимальный интервал идентификации в секундах;

• Minimum Interval Value (sec) – минимальный интервал и дентификации в секундах;

• Limit Output Data - окно контроля, позволяющее ограничить объем выходных данных (только при включенном окне контроля будут доступны два следующих окна редактирования текста);

• Maximum Plant Output – максимальное значение выходного сигнала;

• Minimum Plant Output - минимальное значение выходного сигнала;

• Simulink Plant Model – задание модели Simulink с указанием входных и выходных портов, используемых при нейросетевой модели управляемого процесса;

• Browse - кнопка, позволяющая набрать любую модель из числа доступных (в рассматриваемом примере это модель магнитной подушки ballrepel0);

• Generate Training Data – кнопка запуска процесса генерации обучающей последовательности;

• Import Data – импорт обучающей последовательности из рабочей области или файла данных (в рассматриваемом примере эти данные накоплены в МАТ – файлах);

• Параметры обучения:

• Training Epochs – количество циклов обучения;

• Training function – задание обучающей функции;

• Use Current Weights- окно контроля, позволяющее подтвердить использование текущих весов нейронной сети;

• Use Validation / Testing for Training – выбор этих окон контроля означает, что 25 % данных из обучающей последовательности будет использовано для формирования контрольного и тестового множеств соответственно.

Выбор процедуры Generate Training Data приведет к тому, что будет запущена программа генерации обучающей последовательности на интервале 100 секунд для модели ballrepel0.mdl. При этом программа генерирует обучающие данные путем воздействия ряда случайных ступенчатых сигналов на модель Simulink управляемого процесса. Графики входного и выходного сигналов объекта управления выводятся на экран. По завершении генерации обучающей последовательности пользователь может отказаться от сгенерированных данных (Reject Data) или их принять (Accept Data). Если пользователь принимает данные, то приложение возвращает к измененному окну (рис. 7).

Рис. 7.

После выполнения операции идентификации часть окон недоступны, а кнопка Generate Training Data заменена кнопкой Erase Generated Data, что позволяет удалить сгенерированные данные. В окне фрейма содержится сообщение: «Обучающая последовательность состоит из 100000 замеров. Можно начинать обучение нейронной сети». Для обучения нейронной сети следует воспользоваться кнопкой Train Network (обучить сеть). Начнется обучение нейросетевой модели. После завершения обучения его результаты отображаются на графиках (рис. 8 а, б).

а б

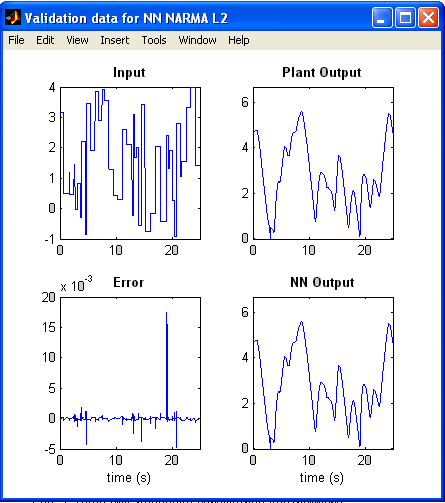
Рис. 8 а,б. Результаты обучения (а) и тестирования (б).

Текущее состояние отмечено в окне Plant Identification сообщением «Обучение завершено. Можно сгенерировать или импортировать новые данные, продолжить обучение или сохранить полученные результаты, выбрав кнопки OK или Apply». В результате параметры нейросетевой модели управляемого процесса будут введены в блок NN NARMA-L2 – Controller системы Simulink.

Выбрав опцию Start из меню Simulation, можно начать моделирование. В процессе моделирования выводятся графики входа и выхода управляемого процесса (рис. 9).

Рис. 9.

Из анализа полученных данных следует, что реакция системы управления на ступенчатые воздействия со случайной амплитудой вполне удовлетворительна, имеет колебательный характер с достаточно быстрым затуханием. На интервале 5 секунд все воздействия эффективно отрабатываются. Таким образом, регулятор NARMA – L2, реализованный в виде нейронной сети, можно использовать для управления магнитной подушкой.

Рабочее задание

1. В соответствии с изложенным выше описанием демонстрационного примера управления магнитной подушкой выполнить этапы по идентификации и синтеза нейросетевой модели регулятора NARMA-L2 с помощью команды narmamaglev, используя командное окно системы Matlab 6.5.

2. В соответствии с вариантом задания (по указанию преподавателя) построить математическую модель для исследования переходного процесса в электрической цепи с двумя накопителями энергии электрического и магнитного поля. По уравнениям электрического состояния цепи в системе Simulink составить ее динамическую модель, в которой присутствуют блоки генерации входного сигнала и отображения графических зависимостей напряжения на конденсаторе и тока в индуктивности катушки. Сохранить динамическую модель в каталоге с расширением *. mdl, например, Model.mdl.

3. Для подсоединения модели к нейроконтроллеру NARMA-L2 заменить блоки генерации входного сигнала и отображения результата на входном (In) и выходном (Out) портах. Модель сохранить отдельно под другим именем *. mdl, например, Perehod.mdl.

4. Командой narmamaglev в командной строке Matlab вызвать модель Magnet Levitation. Эта модель доступна на экране терминала при активизации блока Plant в окне Model Browser.

5. В модель системы контроллера внести изменения. Из файла Perehod.mdl скопировать динамическую модель и перенести ее на место исходной динамической модели управления магнитной подушкой в системе Simulink. Маску модели в системе Simulink можно заменить так, как показано на рис. 10.

6. Выполнить этапы по идентификации и синтезу нейросетевой модели регулятора NARMA-L2 и сопоставить результаты обучения нейронной сети с результатами математического моделирования переходного процесса в исследуемой электрической цепи в пакете Matlab с созданием файла с расширением *.m.

Рис. 10.

Вопросы к защите

1. Поясните принцип работы регулятора NARMA-L2 на примере управления магнитной подушкой.

2. Опишите окно идентификации объекта управления, функции и параметры для его задания.

3. Объясните необходимость применения процедуры Generate Training Data.

4. Применение нейронных сетей для решения задач управления предусматривает два этапа проектирования. В чем смысл этих этапов?

5. Сопоставьте результаты обучения нейронной сети с результатами математического моделирования переходного процесса в исследуемой электрической цепи в пакете Matlab.

Литература

1. Андрейчиков А.В., Андрейчикова О.Н. Интеллектуальные информационные системы: Учебник.- М.: Финансы и статистика, 2004. – С. 344 – 353.

2. Интеллектуальные информационные системы. Конспект лекций / Авторы - сост: В.З Ковалев, А.С. Татевосян, А.А. Татевосян. – Омск: Изд-во ОмГТУ, 2005.- С. 81 - 94.

3. Нейронные сети. MATLAB 6 / Под общ. ред. В.Г. Потемкина. – М.: ДИАЛОГ-МИФИ, 2001. – 384 с.