5 Электромагнетизм

5.1 Основные формулы

Вращающий момент сил зависит как от свойств поля в данной точке, так и от свойств рамки:

где 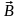— вектор магнитной индукции, являющейся количественной характеристикой магнитного поля;

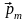— вектор магнитного момента рамки с током.

Для плоского контура с током

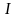
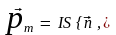
где S — площадь поверхности контура (рамки);

— единичный вектор нормали к поверхности рамки.

Магнитная индукция в данной точке однородного магнитного поля определяется максимальным вращающим моментом, действующим на рамку с магнитным моментом, равным единице, когда нормаль к рамке перпендикулярна направлению поля:

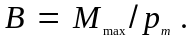
Для однородной изотропной среды вектор магнитной индукции связан с вектором напряженности следующим соотношением:

где 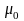— магнитная постоянная;

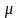—магнитная проницаемость среды,

Закон Био — Савара — Лапласа для проводника с током I, элемент которого dl создает в некоторой точке индукцию поля , записывается в виде

где 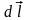— вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током;

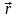— радиус-вектор, проведенный из элемента dl проводника в точку поля;

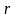— модуль радиуса-вектора .

Модуль вектора определяется выражением

где — угол между векторами и .

• магнитное поле прямого тока

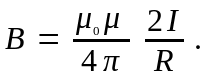
• магнитное поле в центре кругового проводника с током

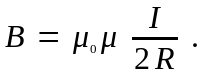
Сила 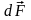, с которой магнитное поле действует на элемент проводника dl с током, находящегося в магнитном поле, прямо пропорциональна силе тока I в проводнике и векторному произведению элемента длиной проводника на магнитную индукцию :

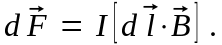
Модуль силы Ампера вычисляется по формуле:

где — угол между векторами и .

Два параллельных тока одинакового направления притягиваются друг к другу с силой:

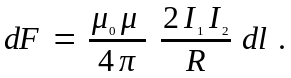
Если токи имеют противоположные направления, то, используя правило левой руки, можно показать, что между ними действует сила отталкивания.

Сила, действующая на электрический заряд Q, движущийся в магнитном поле со скоростью 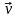, называется силой Лоренца и выражается формулой

где 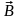— индукция магнитного поля, в котором заряд движется.

Модуль силы Лоренца равен:

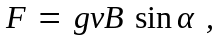
где — угол между и .

Закон электромагнитной индукции Фарадея: какова бы ни была причина изменения потока магнитной индукции, охватываемого замкнутым проводящим контуром, возникающая в контуре э. д. с.

= –

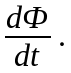
Магнитный поток, сцепленный с рамкой площадью S, в любой момент времени t, равен:

где = 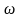t — угол поворота рамки в момент времени t (начало отсчета выбрано так, чтобы при t = 0 = 0).

При вращении рамки в ней будет возникать переменная э. д. с. индукции,

изменяющаяся со временем по гармоническому закону:

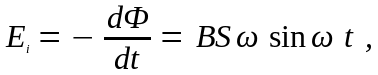
При 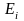максимальна, т.е.

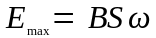
Сцепленный с контуром магнитный поток Ф пропорционален току I в контуре:

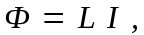
где коэффициент пропорциональности L называется индуктивностью контура.

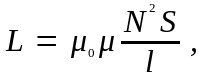
где N – число витков;

S – площадь контура.

Э.Д.С. самоиндукции вычисляется по формуле:

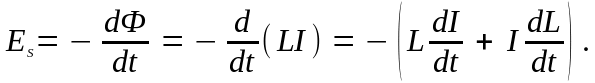
Если контур не деформируется и магнитная проницаемость среды не изменяется, то L = const и

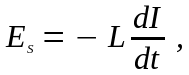
Коэффициентом трансформации называется отношение числа витков N₂/N₁, во вторичной обмотке трансформатора к числу витков в первичной обмотке:

т. е. токи в обмотках обратно пропорциональны числу витков в этих обмотках.

Если N₂/N₁ > 1, то имеем дело с повышающим трансформатором; если N₂/N₁ < l, то имеем дело с понижающим трансформатором.

Энергия магнитного поля, связанного с контуром, определяется: