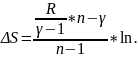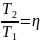2 Основы термодинамики

2.1 Основные формулы

Количество вещества тела (системы):

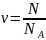
где N – число структур элементов (молекул, атомов, ионов и т.п.), составляющих тело (систему);

N_A – постоянная Авогадро (N_A = 6.02 *10²³ моль^-1).

Молярная масса вещества:

M = m/

где m – масса однородного тела (системы);

– количество вещества этого тела.

Уравнение Менделеева – Клапейрона ( уравнение состояния идеального газа):

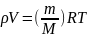
где m – масса газ;

М – молярная масса газа;

R – молярная газовая постоянная;

V – объем газа;

Т – термодинамическая температура.

Объединенный газовый закон (m = const):

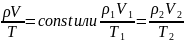
где ρ₁, V₁, T₁ – давление, объем и температура газа в начальном состоянии;

ρ₂, V₂, T₂ – те же величины в конечном состоянии.

Концентрация молекул:

n = N/V

где N – число молекул, содержащихся в данной системе;

– плотность вещества;

V – объем системы.

Формула справедлива не только для газов, но и для любого агрегатного состояния вещества.

Основное уравнение кинетической теории газов:

ρ=3/2 n<ε_n>

где <ε_n> - средняя кинетическая энергия поступательного движения молекулы.

Средняя кинетическая энергия поступательного движения молекулы:

<ε_n> = 3/2 kТ

где k – постоянная Больцмана.

Средняя полная кинетическая энергия молекулы:

<ε_n> = i/2 kТ

где i – число степеней свободы молекулы.

Зависимость давления газа от концентрации молекул и температуры:

p = nkT.

Скорости молекул:

- средняя квадратичная

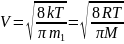– средняя арифметическая

- наиболее вероятная

где m₁ - масса одной молекулы.

Удельные теплоемкости газа при постоянном объеме (С_v) и постоянном давлении (C_p):

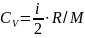
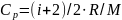
Связь между удельной с и молярной C теплоемкостями:

с = С/M

С = сМ

Уравнение Майера:

С_p + C_v = R

Внутренняя энергия газа:

U = i/2RT(m/M) = m/M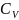 T

Первое начало термодинамики:

Q = △U+A

где Q – теплота, сообщенная системе (газу);

△U – изменение внутренней энергии системы;

A – работа, совершенная системой против внешних сил.

Работа расширения газа:

А = в общем случае

А = p(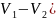 при изобарном процессе

А = m/ при изотермическом процессе

A = - △U = - m/M

при адиабатном процессе, где γ =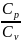 - показатель адиабаты.

Уравнение Пуассона, связывающее параметры идеального газа при адиабатном процессе:

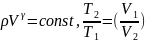^γ-1

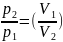^γ ,

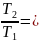
Термический КПД цикла:

η =

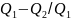
где 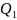- теплота, полученная рабочим телом от теплоотдатчика;

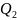– теплота, переданная рабочим телом теплоприемнику.

Термический КПД цикла Карно:

η =

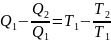
где 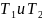– термодинамические температуры теплоотдатчика и теплоприемника.

Коэффициент поверхностного натяжения:

α = F/l или α = △Е/△S

где F – сила поверхностного натяжения, действующая на контур l, ограничивающий поверхность жидкости;

△E – изменение свободной энергии поверхностной пленки жидкости, связанное с изменением площади △S поверхности этой пленки.

2.2 Примеры решения задач

Пример 1.

Азот массой m=0,1 кг был изобарно нагрет от температуры Т₁=200 К до температуры Т₂ = 400 К. Определить работу А, совершенную газом, полученную им теплоту и измене­ние внутренней энергии азота.

Рисунок 5

Дано: m=0,1 кг Т1=200 К Т2 = 400 К µ=28*10-3 кг

A=? ,Q=? , ΔU=?

Решение:

Изобразим процесс на PV - диаграмме (рисунок 5). Работа газа при изоба­рическом расширении:

A = p(V₂-V₁).

Из уравнения Менделеева- Клапейрона:

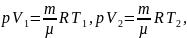
поэтому:

Размерность:

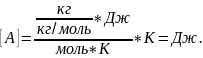
Изменение внутренней энергии газа определяется изменением его температуры:

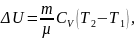
где - молярная теплоемкость газа при постоянном объ­еме;

i - число степеней свободы молекулы (азот - двухатомный газ, поэтому i = 5).

Тогда:

Дж.

Размерность:

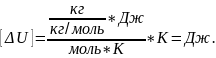
На основании первого начала термодинамики определим теп­лоту, полученную газом:

Дж.

Ответ: A=5,9*10³ Дж, ΔU=14.8*10³ Дж, Q=20,7*10³ Дж.

Пример 2.

В сосуде находится водород массой m = 10 г. При изо­термическом расширении объем водорода увеличивается в два раза. Считая водород идеальным газом, найти приращение его энтропии.

Дано: m = 10 г=10-2кг V2=2V1 µ=2*10-3 кг

ΔS=?

Решение:

Согласно второму началу термодинами­ки изменение энтропии определяется на­чальным и конечным состоянием системы. Если процесс перехода системы из началь­ного состояния в конечное обратимый, то:

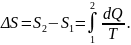
По первому началу термодинамики:

dQ=dU+dA .

При изотермическом процессе (Т = const) изменение внутренней энергии равно нулю (dU= 0), поэтому:

dQ=dA=p*dV ,

Из уравнения Менделеева - Клапейрона:

,

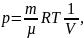
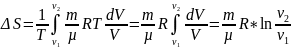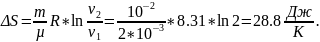
Размерность:

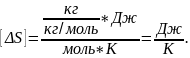
Ответ: ΔS=28.8 .

Пример 3.

Один моль идеального газа с показателем адиабаты γ совершает политропический процесс, в результате которого аб­солютная температура газа Т возрастает в η раз. Показатель по­литропы равен η. Найти приращение энтропии газа ΔS.

Дано: η,γ

ΔS=?

Решение:

Приращение энтропии при обратимом процессе:

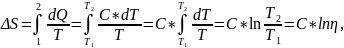
где С - молярная теплоемкость идеального газа в этом процессе.

Политропический процесс описывается уравнением:

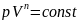
где n-показатель палитры;

p-давление газа;

V-объем, занимаемый газом.

Определим С из выражения для показателя палитры:

,

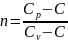где C_p, С_v - молярные теплоемкости при постоянном давлении и постоянном объеме соответственно.

Тогда:

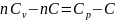
Отсюда:

Так как

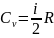и , то ,

где i - число степеней свободы;

R - универсальная газовая постоянная.

Определим i:

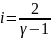
Тогда:

Следовательно, молярная теплоемкость С идеального газа в этом процессе:

Приращение энтропии:

Размерность:

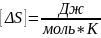
Ответ: