Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Оренбургский государственный университет»

И.Н. Анисина, А.А. Огерчук, Т. И. Пискарёва

СБОРНИК ЗАДАЧ ПО ФИЗИКЕ

Рекомендовано Ученым советом федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Оренбургский государственный университет» в качестве учебного пособия для студентов заочного отделения технических специальностей

Оренбург

2012

УДК 53(075.8)

ББК 22.3я7

А67

Рецензент –

Анисина, И. Н.

А 67 Сборник задач по физике: учебное пособие / И.Н.Анисина, А.А. Огерчук, Т.И. Пискарёва; – Оренбургский гос. ун – т. Оренбург : ОГУ, 2012. – 106 с.

Учебное пособие содержит методику решения задач по общей физике и предназначено для выполнения контрольных работ по дисциплине «Физика» студентами заочного отделения технических специальностей.

УДК 53(075.8)

ББК 22.3я7

©Анисина А.А.,

Огерчук А.А..,

Пискарёва Т.И., 2012

© ОГУ, 2012

Содержание

Общие методические указания к решению задач 3

1 Физические основы механики 4

1.1 Основные формулы 4

1.2 Примеры решения задач 9

2 Основы термодинамики 18

2.1 Основные формулы 18

2.2 Примеры решения задач 21

3 Электростатика 26

3.1 Основные формулы 26

3.2 Примеры решения задач 31

4 Постоянный ток 46

4.1 Основные формулы 46

4.2 Примеры решения задач 49

5 Электромагнетизм 54

5.1 Основные формулы 54

5.2 Примеры решения задач 58

6 Задачи для самостоятельного решения 76

Список использованных источников 102

Приложение А (обязательное) 103

Общие методические указания к решению задач

Решение задач требует знания физических законов. Поэтому, прежде чем приступить к решению задач, необходимо изучить соответствующие темы курса физики по рекомендуемым учеб­ным пособиям. При решении задач необходимо пользоваться сле­дующей схемой:

1. Записать полностью условие задачи. Выразить все величи­ны, входящие в условие в Международной системе единиц СИ.

2. Осмыслить физическую сущность задачи, представив ее на­глядно в виде четкого рисунка, на котором, хотя бы условно, указать все параметры, характеризующие явления, на основе кото­рых построено условие задачи.

3. Указать основные законы и формулы, на которых базируется условие задачи, разъяснить буквенные обозначения, употребляе­мые при написании формул. Если при решении задачи применяется формула, полученная для частного случая, не выражающая какой-нибудь физический закон или не являющаяся определением какой-нибудь физической величины, то ее следует вывести. Пояснения должны быть краткими, но исчерпывающими.

4. Решить задачу сначала в общем виде, то есть в буквенных обозначениях, заданных в условии задачи и взятых из таблиц.

5. Подставив в рабочую формулу размерности, убедиться в правильности размерности искомой величины.

6. Подставить в конечную формулу числовые значения. При вычислениях соблюдать правила приближенных вычислений и округлений.

1 Физические основы механики

1.1 Основные формулы

Кинематическое уравнение движения материальной точки (центра масс твёрдого тела) вдоль оси x

X = f(x)

где f(x) – некоторая функция времени.

Проекция средней скорости на ось x

(v_x) = ∆X/∆t

Средняя путевая скорость

(v) = ∆s/∆t

где ∆s – путь, пройденный за интервал времени ∆t. Путь ∆s в отличие от разности координат ∆ x= x₂- x₁ не может убывать и принимать отрицательные значения, т.е. ∆s>0

Проекция мгновенной скорости на ось x

v_x = dx/dt

Проекция среднего ускорения на ось x

a_x = dv_x/dt

Проекция мгновенного ускорения на ось x

a_x = dv_x/dt

Кинематическое уравнение движения материальной точки по окружности:

φ = f(t), r = R = const

Модуль угловой скорости: ω = dφ/dt

Модуль углового ускорения: ε = dω/dt

Связь между модулями линейных и угловых величин, характеризующих движение точки по окружности:

v = ωR,

a_t = εR,

a_n = ω²R

где v – модуль линейной скорости;

a_t и a_n – модули тангенциального и нормального ускорений;

ω – модуль угловой скорости;

ε – модуль углового ускорения;

R – радиус окружности.

Модуль полного ускорения

а = a_t²+ a_n²

,

Угол между полным a и нормальным a_n ускорениями

α = arccos(a_n/a)

Импульс материальной точки массой m, движущейся со скоростью v: p=mv

Второй закон Ньютона:

dp = Fdt,

где F – результирующая сила, действующая на материальную точку.

Силы рассматриваемые в механике:

а) сила упругости

F = -kx

где k – коэффициент упругости (в случае пружины - жёсткость);

x – абсолютная деформация;

б) сила тяжести

P = mg

в) сила гравитационного взаимодействия

F = Gm₁m₂/r²

где G – гравитационная постоянная;

m₁ и m₂ – массы взаимодействующих тел;

r – расстояние между телами (тела рассматриваются как материальные точки).

г) сила трения (скольжения)

F = μN,

где μ – коэффициент трения;

N – сила нормального давления

Закон сохранения импульса:

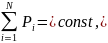
или для двух тел (i=2)

m₁v₁+m₂v₂ = m₁u₁+ m₂u₂

где v₁ и v₂ – скорости тел в начальный момент времени;

u₁ и u₂ – скорости тех же тел в конечный момент времени.

Кинетическая энергия тела, движущегося поступательно:

T = mv²/2, или T = p² /(2m)

Потенциальная энергия:

а) упругодеформированной пружины

П = 1/2kx²,

где k – жёсткость пружины;

x – абсолютная деформация.

б) гравитационного взаимодействия

П = -Gm₁ m₂/r

где G – гравитационная постоянная;

m₁ и m₂ – массы взаимодействующих тел;

r – расстояние между ними (тела рассматриваются как материальные точки).

в) тела, находящегося в однородном поле силы тяжести

П = mgh

где g – ускорение свободного падения;

h – высота тела над уровнем, принятым за нулевой (формула справедлива при условии g<<R, где R – радиус Земли).

Закон сохранения механической энергии:

E = T+П = const.

Работа А, совершаемая результирующей силой, определяется как мера изменения кинетической энергии материальной точки:

А = ∆Т = Т₂ – Т₁

Основное уравнение динамики вращательного движения относительно неподвижной оси z:

M_z = J_zε

где M_z – результирующий момент внешних сил относительно оси z, действующих на тело;

ε – угловое ускорение;

J_z – момент инерции относительно оси вращения.

Моменты инерции некоторых тел массой m относительно оси z проходящей через центр масс:

а) стержня длинной l относительно оси, перпендикулярной стержню

J_z = 1/12ml²

б) обруча (тонкостенного цилиндра) относительно оси, перпендикулярной плоскости обруча (совпадающей с осью цилиндра)

J_z = mR²

где R – радиус обруча (цилиндра).

в) диска радиусом R относительно оси, перпендикулярной плоскости диска

J_z = 1/2mR²

Проекция на ось z момента импульса тела, вращающегося относительно неподвижной оси z:

L_z = J_zω

где ω – угловая скорость тела.

Закон сохранения момента импульса систем тел, вращающихся вокруг неподвижной оси z:

J_zω = const,

где J_z – момент инерции тел относительно оси z;

ω – угловая скорость вращения тел системы вокруг оси z.

Кинетическая энергия тела, вращающегося вокруг неподвижной оси z.

Т = J_zω²/2.