Указания к задаче 4

Кручение – это такой вид деформации стержня, при котором в его поперечных сечениях возникает единственный внутренний силовой фактор – крутящий момент.

Внешние моменты, воздействующие на вал, называются скручивающими.

Расчет вала на прочность начинается с построения эпюры крутящего момента и отыскания опасного сечения.

Касательные напряжения при кручении определяются по формуле:

,

где Т_КР – крутящий момент, действующий в сечении;

 - радиус той точки поперечного сечения, в которой определяются напряжения;

I_p – полярный момент инерции сечения.

Условие прочности при кручении записывается следующим образом:

.

где W_p – полярный момент сопротивления сечения.

Угол закручивания вала определяется по формуле:

,

где l – длина вала;

G – модуль упругости второго рода.

Условие жесткости при кручении записывается следующим образом:

.

Полярный момент инерции и полярный момент сопротивления круглого сечения определяются по формулам соответственно:

, ,

где d – диаметр вала.

Полярный момент инерции и полярный момент сопротивления кольцевого сечения определяются по формулам соответственно:

, ,

где D – внешний диаметр вала;

;

d – внутренний диаметр вала.

ПРИМЕР

Для вала, изображенного на рис. 9, подобрать поперечное сечение круглой, кольцевой и прямоугольной форм, если Т₁ =600 Нм, Т₂ =1000 Нм, Т₃ = =800Нм, Т₄ = 1300 Нм, Т₅ =1600Нм,  = 0,7, h/b = 2, [] =100МПа. Построить эпюру углов закручивания для вала круглого поперечного сечения.

Решение

1. Строим эпюру крутящего момента со свободного конца вала и определяем опасное сечение

АС

СД

Рисунок 9.

ДЕ

ЕК

КВ

Из эпюры крутящих моментов (рис. 9) видно, что опасным, является участок КВ, максимальное значение крутящего момента Т_{кр max}= 1700 Нм.

2. Подбираем поперечное сечение вала

7.1) Круглое сечение

Условие прочности при кручении:

Принимаем d = 45 мм.

7.2) Кольцевое сечение

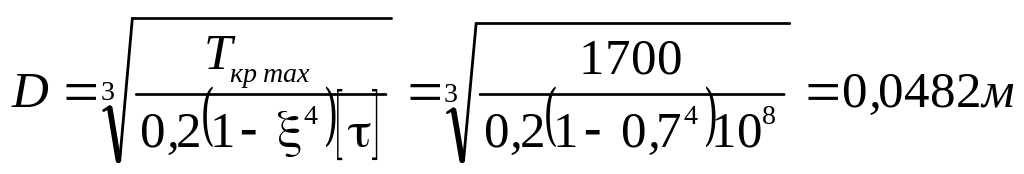
Принимаем D = 50 мм, тогда мм.

7.3) Прямоугольное сечение

Для прямоугольного сечения с отношением h/b = 2  = 0,493.

Тогда м.

3. Строим эпюру углов закручивания

Найдем момент инерции для круглого сечения:

м⁴.

4. Сравним веса валов

Найдем площадь поперечного сечения для каждого из валов: круглого, кольцевого, прямоугольного.

Указания к задаче 5

Определение положения центра тяжести сложного сечения

Координаты центра тяжести любой сложной фигуры можно определить по формулам:

, ,

где S_x, S_y – статические моменты площади сечений простых фигур, составляющих сложную фигуру;

S – площадь фигуры.

Сумма статических площадей простых фигур определяется по формуле:

, ,

где S_i – площадь i-той простой фигуры;

x_i, y_i – координаты центра тяжести i-той простой фигуры.

ПРИМЕР 1

Определить положение центра тяжести фигуры, показанной на рис. 10.

Рисунок 10.

1. Выбираем произвольные оси координат

2. Разбиваем сечение на простейшие фигуры

3. Находим площадь каждой из фигур

мм²;

мм².

4. Определяем статические моменты площади

мм³

мм³

5. Находим координаты центра тяжести

мм;

мм.

Определение моментов инерции сечения при параллельном переносе осей

Пусть известны все геометрические характеристики сечения относительно исходных осей х, у (рис. 11). Определим моменты инерции относительно параллельных им осей х_С, у_С, проходящих через центр тяжести сечения.

Р

исунок 11.

,

,

,

где I_x, I_y – осевые моменты инерции относительно исходных осей;

I_xy – центробежный момент инерции относительно исходных осей;

I_xc, I_yc – осевые моменты инерции относительно центральных осей;

I_xcyc – центробежный момент инерции относительно центральных осей;

a, b – расстояние между осями.

Определение моментов инерции сечения при повороте осей

Известны все геометрические характеристики сечения относительно центральных осей х_С, у_С (рис. 12). Определим моменты инерции относительно осей х₁, у₁, повернутых относительно центральных на некоторый угол .

Рисунок 12.

,

,

,

где I_x1, I_y1 – осевые моменты инерции относительно осей х₁, у₁;

I_x1y1 – центробежный момент инерции относительно осей х₁, у₁.

Определение положения главных центральных осей инерции

Положение главных центральных осей инерции сечения определяется по формуле:

,

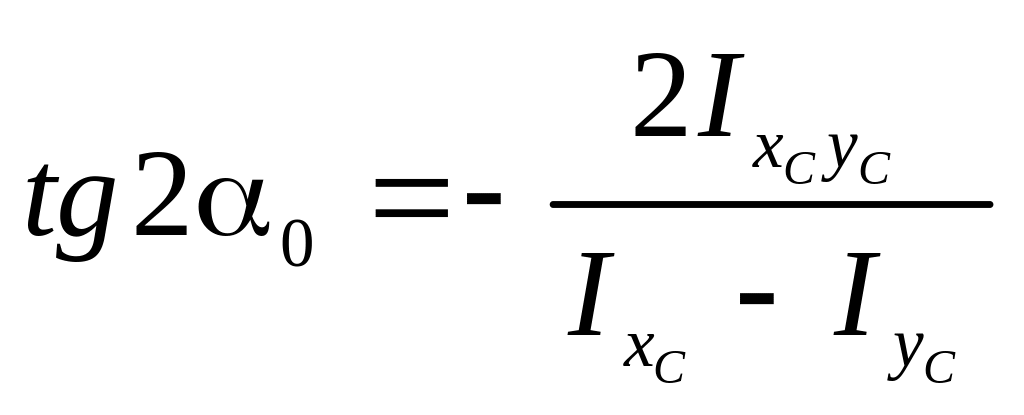где ₀ – угол между центральными и главными осями инерции.

Определение главных моментов инерции

Главные моменты инерции сечения определяются по формуле:

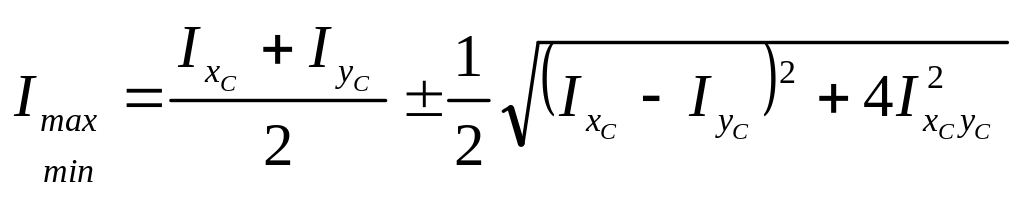
Последовательность расчета сложного сечения

1. Разбить сложное сечение на простейшие геометрические фигуры [S₁, S₂,…;x₁, y₁; x₂, y₂, …]

2. Выбрать произвольные оси XOY.

3. Определить положение центра тяжести сечения [x_c, y_c].

4. Провести центральные оси X_cOY_c.

5. Вычислить моменты инерции Ix_c, Iy_c, используя теорему параллельного переноса осей.

6. Вычислить центробежный момент инерции Ix_cy_c.

7. Определить положение главных осей инерции tg2₀.

8. Вычислить главные моменты инерции I_max, I_min.