
- •3. Динамика
- •Исходные данные
- •Дифференциальные уравнения точки принимают вид:
- •Проекции скорости на оси координат определяются уравнениями (3.5).
- •Задание д2 Применение теоремы об изменении кинетической энергии к изучению движения механической системы
- •Задание д4 Применение принципа возможных перемещений для определения условий равновесия
- •Сборник заданий для контрольных работ по теоретической механике
- •443100, Г. Самара, ул. Молодогвардейская, 244. Главный корпус
- •443100, Г. Самара, ул. Молодогвардейская, 244. Корпус № 8
Задание д2 Применение теоремы об изменении кинетической энергии к изучению движения механической системы
Механизм начинает двигаться из состояния покоя под действием заданных сил: постоянной силы F, постоянного вращающего момента Мвр и сил тяжести. Сила и момент действуют на одно из тел, как показано на рисунке. Зная массы тел m1, m2, m3, m4; радиусы r и R малых и больших окружностей колёс; радиусы инерции ступенчатых колёс ρ, определить какую скорость будет иметь тело 1 после того, как оно переместится на расстояние S=3м. Коэффициент трения скольжения для всех вариантов, где груз скользит по плоскости, f=0,05. Сопротивлением качению пренебречь. Качение колёс происходит без скольжения. Численные значения всех величин даны в таблице 3.2.
П ример.
Применение
теоремы об изменении кинетической
энергии к изучению движения механической
системы
Механизм движется из состояния покоя.
Определить скорость тела 1 после его
перемещения на расстояние S=0,5м.
Дано: массы тел m1=10кг,
m2=30кг,
m3=15кг,
m4=20кг,
радиусы
колёс r2=0,2м,
R2=0,4м,
r3=0,25м,
r4=0,25м
, радиус инерции тела 2 ρ2=0,25м,
сила F=100Н,
Мвр=20м.
ример.
Применение
теоремы об изменении кинетической
энергии к изучению движения механической
системы
Механизм движется из состояния покоя.
Определить скорость тела 1 после его
перемещения на расстояние S=0,5м.
Дано: массы тел m1=10кг,
m2=30кг,
m3=15кг,
m4=20кг,
радиусы
колёс r2=0,2м,
R2=0,4м,
r3=0,25м,
r4=0,25м
, радиус инерции тела 2 ρ2=0,25м,
сила F=100Н,
Мвр=20м.
Рис.3.3 Схема
механизма
Решение
Кинематика механизма. Выразим основные кинематические параметры звеньев механизма через искомую скорость v1. Из рисунка видно, что тело 1 движется поступательно, тела 2 и 3 вращаются, а тело 4 движется плоскопараллельно. Угловая скорость колеса 2 определяется из условия равенства скоростей точек контакта звеньев 1 и 2.
V1=ω2·r2
ω2=![]() .
(3.6)
.
(3.6)
И з
аналогичного условия равенства скоростей
точек контакта колёс 2 и 3 находим угловую
скорость колеса 3. Так как ω2·R2=
ω3·r3,
то
з
аналогичного условия равенства скоростей
точек контакта колёс 2 и 3 находим угловую
скорость колеса 3. Так как ω2·R2=
ω3·r3,
то
ω3=![]() .
(3.7)
.
(3.7)
Рис 3.4 Кинематическая схема.
.
С хемы
механизмов
хемы
механизмов
1
|
2
4 |
3
|
|
5
|
6
F |
7
|
8 |
9
F
Мвр
1
2
3
4
|
1 |
11
|
1 |
13
|
1 |
1
|
1
Мвр |
1
|
1 |
19
|
2 |
2
|
2 |
2
|
2 |
25
|
2
3
Мвр |
2
3
|
2 |
2
|
3
1
2
3
F
Мвр |
3
|
3 |
3
|
3 |
Исходные данные.
Таблица 3.2
№ вар. |
№ рис. |
m1 , кг |
m2 , кг |
m3, кг |
m4, кг |
r2 , м |
R2, м |
r3, м |
R3, м |
ρ2, м |
ρ3, м |
F, Н |
Мвр, Нм |
1 |
1 |
40 |
20 |
20 |
30 |
0,5 |
- |
0,2 |
- |
- |
- |
10 |
40 |
2 |
2 |
30 |
10 |
30 |
25 |
0,2 |
- |
0,2 |
0,4 |
- |
0,3 |
110 |
30 |
3 |
3 |
20 |
20 |
10 |
40 |
0.5 |
- |
0,3 |
- |
- |
- |
60 |
30 |
4 |
4 |
20 |
20 |
10 |
20 |
0,4 |
- |
0,2 |
- |
- |
- |
100 |
40 |
5 |
5 |
23 |
30 |
20 |
50 |
0,5 |
- |
0,3 |
- |
- |
- |
710 |
40 |
6 |
6 |
20 |
100 |
30 |
30 |
0.3 |
- |
0.6 |
- |
- |
- |
120 |
50 |
7 |
7 |
10 |
15 |
30 |
20 |
0,3 |
- |
0,2 |
0,4 |
- |
0,3 |
100 |
70 |
8 |
8 |
25 |
10 |
15 |
15 |
0. 3 |
- |
0,25 |
0,5 |
- |
0,4 |
50 |
50 |
9 |
9 |
29 |
10 |
20 |
- |
0,25 |
- |
0,4 |
- |
- |
- |
100 |
25 |
10 |
10 |
20 |
15 |
30 |
- |
0,3 |
- |
0,3 |
0,5 |
- |
0,4 |
200 |
50 |
11 |
11 |
10 |
20 |
10 |
- |
0,2 |
0,5 |
0,3 |
- |
0,3 |
- |
60 |
40 |
12 |
12 |
10 |
15 |
10 |
15 |
0,2 |
0,4 |
0,3 |
- |
0,3 |
- |
50 |
120 |
.13 |
13 |
5 |
22 |
12 |
10 |
0,2 |
- |
0,2 |
0,5 |
- |
0,4 |
40 |
550 |
14 |
14 |
20 |
20 |
10 |
10 |
0,2 |
0,5 |
0,3 |
- |
0,4 |
- |
100 |
20 |
15 |
15 |
35 |
25 |
20 |
- |
0,1 |
- |
0,3 |
- |
- |
- |
100 |
40 |
16 |
16 |
10 |
24 |
25 |
- |
0,15 |
- |
0,4 |
- |
- |
- |
100 |
30 |
17 |
17 |
35 |
22 |
10 |
10 |
0,1 |
0,3 |
0,2 |
- |
- |
- |
150 |
30 |
18 |
18 |
25 |
10 |
25 |
- |
0,2 |
- |
0,3 |
- |
- |
- |
60 |
10 |
19 |
19 |
15 |
20 |
50 |
20 |
0,3 |
- |
0,2 |
0,4 |
- |
0,3 |
70 |
50 |
20 |
20 |
35 |
10 |
15 |
- |
0,2 |
- |
- |
- |
- |
- |
120 |
50 |
21 |
21 |
10 |
10 |
20 |
- |
0,2 |
- |
0,3 |
- |
- |
- |
100 |
35 |
22 |
22 |
20 |
10 |
20 |
- |
0,25 |
- |
0,4 |
- |
- |
- |
100 |
30 |
23 |
23 |
20 |
15 |
30 |
- |
0,2 |
- |
0,2 |
0,5 |
- |
0,3 |
200 |
10 |
24 |
24 |
20 |
10 |
20 |
- |
0,3 |
0,6 |
0,3 |
- |
0,4 |
- |
230 |
40 |
25 |
25 |
30 |
15 |
20 |
- |
0,2 |
- |
0,3 |
- |
- |
- |
0 |
35 |
26 |
26 |
30 |
15 |
30 |
- |
0,2 |
- |
0,2 |
0,4 |
- |
0,3 |
100 |
40 |
27 |
27 |
10 |
25 |
20 |
- |
0,3 |
0,6 |
0,2 |
- |
0,4 |
- |
150 |
25 |
28 |
28 |
12 |
20 |
18 |
- |
0,2 |
0,4 |
0,2 |
- |
0,4 |
- |
20 |
70 |
29 |
29 |
10 |
15 |
20 |
- |
0,3 |
0,6 |
0,2 |
- |
0,4 |
- |
100 |
15 |
№ вар. |
№ рис. |
m1 , кг |
m2 , кг |
m3, кг |
m4, кг |
r2 , м |
R2, м |
r3, м |
R3, м |
ρ2, м |
ρ3, м |
F, Н |
Мвр, Нм |
30 |
30 |
5 |
15 |
25 |
- |
0,2 |
- |
0,2 |
0,4 |
- |
0,3 |
10 |
80 |
31 |
31 |
39 |
12 |
20 |
- |
0,3 |
- |
0.3 |
- |
- |
- |
0 |
20 |
32 |
32 |
20 |
15 |
10 |
- |
0,2 |
0,4 |
0,3 |
- |
0,3 |
- |
40 |
10 |
33 |
33 |
14 |
18 |
20 |
10 |
0,3 |
- |
0,3 |
- |
- |
- |
10 |
10 |
34 |
34 |
10 |
15 |
12 |
4 |
0,25 |
0,5 |
0,3 |
- |
0,4 |
- |
100 |
40 |
35 |
1 |
50 |
20 |
10 |
30 |
0,5 |
- |
0.2 |
- |
- |
- |
0 |
50 |
36 |
2 |
26 |
10 |
30 |
15 |
0,2 |
- |
0,2 |
0,4 |
- |
0,3 |
110 |
0 |
37 |
3 |
16 |
20 |
10 |
30 |
0.5 |
- |
0,2 |
- |
- |
- |
60 |
0 |
38 |
4 |
26 |
20 |
10 |
20 |
0,4 |
- |
0,2 |
- |
- |
- |
0 |
40 |
39 |
5 |
34 |
40 |
20 |
50 |
0,5 |
- |
0,25 |
- |
- |
- |
700 |
60 |
40 |
6 |
18 |
10 |
30 |
20 |
0.3 |
- |
0,6 |
- |
- |
- |
120 |
0 |
41 |
7 |
12 |
10 |
20 |
20 |
0,3 |
- |
0,2 |
0,4 |
|
0,3 |
40 |
170 |
42 |
8 |
20 |
19 |
18 |
10 |
0. 3 |
- |
0,25 |
0,5 |
- |
0,4 |
50 |
0 |
43 |
9 |
15 |
25 |
10 |
- |
0,2 |
- |
0,5 |
- |
- |
- |
100 |
50 |
44 |
10 |
30 |
10 |
25 |
- |
0,3 |
- |
0,3 |
0,5 |
- |
0,4 |
100 |
50 |
45 |
11 |
10 |
20 |
10 |
- |
0,2 |
0,5 |
0,3 |
- |
0,3 |
- |
40 |
50 |
46 |
12 |
10 |
25 |
15 |
15 |
0,2 |
0,4 |
0,3 |
- |
0,3 |
- |
30 |
120 |
47 |
13 |
5 |
20 |
10 |
10 |
0,2 |
0,3 |
0,5 |
- |
- |
0,4 |
40 |
300 |
48 |
14 |
20 |
20 |
10 |
10 |
0,2 |
0,5 |
0,3 |
- |
0,4 |
- |
100 |
20 |
49 |
15 |
25 |
20 |
25 |
- |
0,1 |
- |
0,3 |
- |
- |
- |
150 |
60 |
50 |
16 |
10 |
22 |
28 |
- |
0,2 |
- |
0,4 |
- |
- |
- |
50 |
70 |
51 |
17 |
40 |
20 |
18 |
10 |
0,1 |
0,3 |
0,2 |
0,25 |
- |
- |
100 |
35 |
52 |
18 |
20 |
10 |
25 |
- |
0,2 |
- |
0,3 |
- |
- |
- |
0 |
8 |
54 |
19 |
15 |
39 |
40 |
20 |
0,2 |
- |
0,2 |
0,4 |
- |
0,3 |
50 |
80 |
55 |
20 |
22 |
12 |
15 |
- |
0,2 |
- |
- |
- |
- |
- |
90 |
15 |
56 |
21 |
15 |
15 |
20 |
- |
0,2 |
- |
0,4 |
- |
- |
- |
100 |
60 |
57 |
22 |
20 |
15 |
25 |
- |
0,25 |
- |
0,4 |
- |
- |
- |
100 |
56 |
58 |
23 |
10 |
15 |
30 |
- |
0,2 |
- |
0,3 |
0,4 |
- |
0,25 |
20 |
0 |
59 |
24 |
12 |
10 |
25 |
- |
0,3 |
0,6 |
0,3 |
- |
0,4 |
- |
100 |
45 |
60 |
25 |
10 |
20 |
20 |
- |
0,25 |
0,5 |
0,3 |
- |
0,3 |
- |
10 |
25 |
61 |
26 |
10 |
10 |
25 |
- |
0,2 |
- |
0,2 |
0,4 |
- |
0,3 |
100 |
90 |
62 |
27 |
10 |
12 |
25 |
- |
0,25 |
0,5 |
0,2 |
- |
0,4 |
- |
100 |
40 |
63 |
28 |
20 |
16 |
18 |
- |
0,2 |
0,4 |
0,2 |
- |
0,4 |
- |
20 |
40 |
64 |
29 |
10 |
12 |
25 |
- |
0,25 |
0,5 |
0,2 |
- |
0,4 |
- |
100 |
40 |
65 |
30 |
5 |
15 |
25 |
- |
0,2 |
- |
0,2 |
0,4 |
- |
0,3 |
0 |
80 |
66 |
31 |
10 |
12 |
20 |
- |
0,3 |
- |
0.3 |
- |
- |
- |
50 |
10 |
67 |
32 |
20 |
15 |
20 |
- |
0,2 |
0,4 |
0,3 |
- |
0,3 |
- |
10 |
20 |
68 |
33 |
10 |
18 |
20 |
10 |
0,3 |
- |
0,3 |
- |
- |
- |
0 |
10 |
69 |
1 |
50 |
20 |
10 |
30 |
0,5 |
- |
0.2 |
- |
- |
- |
0 |
0 |
70 |
2 |
20 |
10 |
30 |
15 |
0,2 |
- |
0,2 |
0,4 |
- |
0,3 |
0 |
30 |
71 |
3 |
20 |
30 |
10 |
30 |
0.5 |
- |
0,3 |
- |
- |
- |
0 |
30 |
72 |
4 |
20 |
24 |
10 |
20 |
0,4 |
- |
0,2 |
- |
- |
- |
100 |
10 |
73 |
5 |
30 |
30 |
10 |
50 |
0,5 |
- |
0,3 |
- |
- |
- |
0 |
150 |
74 |
6 |
10 |
10 |
30 |
20 |
0.3 |
- |
0.6 |
- |
- |
- |
26 |
100 |
75 |
7 |
20 |
10 |
15 |
20 |
0,3 |
- |
0,2 |
0,4 |
|
0,3 |
0 |
150 |
76 |
8 |
20 |
10 |
15 |
10 |
0. 3 |
- |
0,25 |
0,5 |
- |
0,4 |
50 |
120 |
77 |
9 |
15 |
10 |
20 |
- |
0,25 |
- |
0,4 |
- |
- |
- |
0 |
50 |
78 |
10 |
20 |
15 |
30 |
- |
0,3 |
- |
0,3 |
0,5 |
- |
0,4 |
60 |
30 |
79 |
11 |
10 |
20 |
10 |
- |
0,2 |
0,5 |
0,3 |
- |
0,3 |
- |
0 |
40 |
80 |
12 |
10 |
15 |
10 |
20 |
0,2 |
0,4 |
0,3 |
- |
0,3 |
- |
50 |
120 |
81 |
13 |
15 |
25 |
15 |
10 |
0,2 |
0,3 |
0,5 |
- |
- |
0,4 |
10 |
100 |
82 |
14 |
20 |
10 |
10 |
10 |
0,2 |
0,5 |
0,3 |
- |
0,4 |
- |
50 |
100 |
83 |
15 |
30 |
25 |
20 |
- |
0,1 |
- |
0,3 |
- |
- |
- |
15 |
60 |
84 |
16 |
10 |
24 |
25 |
- |
0,15 |
- |
0,4 |
- |
- |
- |
10 |
60 |
85 |
17 |
30 |
25 |
10 |
10 |
0,1 |
0,3 |
0,2 |
- |
- |
- |
0 |
50 |
86 |
18 |
20 |
12 |
22 |
- |
0,2 |
- |
0,4 |
- |
- |
- |
50 |
0 |
87 |
19 |
18 |
22 |
35 |
20 |
0,3 |
- |
0,2 |
0,4 |
- |
0,3 |
40 |
68 |
88 |
20 |
18 |
12 |
15 |
- |
0,2 |
- |
- |
- |
- |
- |
29 |
5 |
89 |
21 |
10 |
15 |
22 |
- |
0,2 |
- |
0,3 |
- |
- |
- |
60 |
0 |
90 |
22 |
20 |
10 |
30 |
- |
0,25 |
- |
0,4 |
- |
- |
- |
10 |
30 |
91 |
23 |
10 |
5 |
20 |
- |
02 |
- |
0,2 |
0,4 |
- |
0,3 |
0 |
20 |
92 |
24 |
10 |
10 |
20 |
- |
0,3 |
0,6 |
0,3 |
- |
0,4 |
- |
39 |
40 |
93 |
25 |
15 |
10 |
15 |
- |
0,2 |
0,2 |
0,4 |
- |
0,3 |
- |
0 |
0 |
94 |
26 |
20 |
15 |
30 |
- |
0,2 |
- |
0,2 |
0,4 |
- |
0,3 |
30 |
60 |
95 |
27 |
12 |
10 |
20 |
- |
0,2 |
0,4 |
0,2 |
- |
0,3 |
- |
40 |
20 |
96 |
28 |
12 |
20 |
20 |
- |
0,2 |
0,4 |
0,2 |
- |
0,4 |
- |
0 |
60 |
97 |
29 |
12 |
10 |
20 |
- |
0,2 |
0,4 |
0,2 |
- |
0,3 |
- |
0 |
20 |
96 |
30 |
5 |
15 |
25 |
- |
0,2 |
- |
0,2 |
0,4 |
- |
0,3 |
10 |
0 |
99 |
31 |
15 |
12 |
25 |
- |
0,3 |
- |
0.3 |
- |
- |
- |
0 |
20 |
100 |
32 |
19 |
20 |
15 |
- |
0,2 |
0,4 |
0,3 |
- |
0,3 |
- |
30 |
15 |
Трос, соединяющий тела 3 и 4, имеет скорость равную Vтр= ω3·r3, так как трос сходит с колеса 3, и Vтр = ω4·2r4, так как он намотан на колесо 4. Иначе говоря, скорость точки колеса, касающейся горизонтального участка троса равна скорости троса. Скорость любой точки колеса 4 вычисляется по правилу
V= ω4·hК, где hК-расстояние от точки до м.ц.с., ω4-угловая скорость колеса 4.
М.ц.с. К находится в точке касания колеса 4 с плоскостью, по которой оно катится без скольжения. Отсюда
ω3·r3=
ω4·2r4,
ω4=![]() = 4V1
(3.8)
= 4V1
(3.8)
Скорость
центра масс колеса 4 VC4=
ω4
r4=![]() =V1
(3.9)
=V1
(3.9)
Мы видим из кинематических расчётов, что все скорости пропорциональны скорости тела 1. Значит соответствующие угловые и линейные перемещения находятся в такой же пропорциональной зависимости.
Угловое перемещение тела 2 выразим через линейное перемещение тела 1:
![]() =
5 ·S1=2,5(рад).
(3.10)
=
5 ·S1=2,5(рад).
(3.10)
Аналогично
SC4=
![]() =S1=0,5м.
(3.11)
=S1=0,5м.
(3.11)
Перейдём к динамике. Применим теорему об изменении кинетической энергии, согласно которой: изменение кинетической энергии механической системы при перемещении её из начального положения в конечное равно сумме работ всех сил, приложенных к этой системе на этом перемещении
Т
– Т0=
![]() .
.
Вычислим кинетическую энергию механизма. Она складывается из кинетических энергий звеньев.
Т=Т1+Т2+Т3+Т4.
Движение механизма начинается из состояния покоя, поэтому Т0=0. Звено 1 движется поступательно, поэтому
Т1=![]() =
5V12.
=
5V12.
Тела 2 и 3 вращаются поэтому
Т2=![]() и Т3=
и Т3=![]() .
.
Моменты
инерции колёс вычислим по формулам: для
тела 2 через радиус инерции![]() =1,875кгм2,
для тела 3 по формуле для однородного
цилиндра
=1,875кгм2,
для тела 3 по формуле для однородного
цилиндра
Iz3=m3r32/2=0,469кгм2
Вычисляем кинетическую энергию колёс: Т2= 46,875 V12, Т2=30V12.
Кинетическая энергия колеса 4 вычисляется по формуле
Т4=![]() =
15 V12
где
=
15 V12
где
![]() =0,625кгм2
=0,625кгм2
и полную кинетическая энергию механизма Т=96,975 V12 (Дж). (3.12)
Т еперь
вычислим работу сил, приложенных к
точкам механической системы. Для этого
покажем силы на схеме.
еперь
вычислим работу сил, приложенных к
точкам механической системы. Для этого
покажем силы на схеме.
Рис 3.5 Силовая схема.
На схеме показаны только внешние силы, потому что для системы, состоящей из твёрдых тел и имеющей идеальные связи, как в нашем случае, работа внутренних сил равна нулю.
Если сила приложена к неподвижной точке, или перпендикулярна направлению перемещения её точки приложения , то работа такой силы тоже равна нулю. С учётом этого, сумма работ всех сил будет равна
![]() .
.
Будем
предполагать, что движение механизма
происходит в направлении действия илы
F.
Тогда![]() F·SC4=100·0,5=50
Дж;
F·SC4=100·0,5=50
Дж;
![]() =-Мвр·φ2=-20·2,5=-50Дж;
=-Мвр·φ2=-20·2,5=-50Дж;
![]() =
m1g·S1=10·9,8·0,5=49Дж;
=
m1g·S1=10·9,8·0,5=49Дж;
Суммарная работа сил равна = 49Дж. (8)
Сумма работ всех сил получилась положительной, значит, мы верно выбрали направление движения. В противном случае нужно направление движения поменять на противоположное.
Приравнивая (7) и (8) 96,975 V12=49, получаем ответ V1=0,505м/с.
Задание Д3 Применение принципа Даламбера (метода кинетостатики) для определения реакций связей
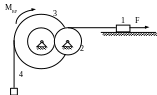
Для получения рисунка к задаче для Вашего варианта нужно совместить схему механизма и схему опоры в точке С. Номер механизма соответствует первой цифре варианта, а номер опоры второй цифре. Например, для варианта 55 рисунок должен выглядеть так, как показано на рис 3.6

Рис.3.6
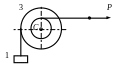
Условие задачи. Механизм, состоящий из грузов 1, (2) и блока 3 движется под действием сил тяжести, вращающего момента Мвр и силы Р, которые показаны на схеме механизма. С помощью принципа Даламбера (метода кинетостатики) установить ускорения грузов 1, (2) и угловое ускорение блока 3. Далее, определить реакции внешних связей для всей конструкции. В таблице 1 даны следующие данные: m1, m2, m3-массы тел; r и R - малый и большой радиусы окружностей блока 3; Iz-момент инерции блока относительно его оси вращения. Из таблицы 3.3 берёте только значение той величины Мвр или Р, которая показана на схеме.
Исходные данные.
Таблица 3.3
№опоры |
m1,кг |
m2,кг |
m3, кг |
r, м |
R, м |
I,кгм2 |
МврНм |
Р,Н |
1 |
2 |
5 |
3 |
0,1 |
0,2 |
0,16 |
0,2 |
20 |
2 |
3 |
2 |
3 |
0,1 |
0,2 |
0,14 |
1,2 |
10 |
3 |
4 |
1 |
2 |
0,15 |
0,3 |
0,19 |
1,5 |
15 |
4 |
1 |
2 |
3 |
0,1 |
0,2 |
0,2 |
3,5 |
5 |
5 |
2 |
1 |
2 |
0,1 |
0,2 |
0,14 |
2 |
15 |
6 |
0,5 |
1 |
1,6 |
0,15 |
0,3 |
0,12 |
1,4 |
10 |
7 |
1 |
0,5 |
2 |
0,2 |
0,3 |
0,2 |
1 |
14 |
8 |
1,5 |
1,2 |
1,8 |
0,15 |
0,2 |
0,11 |
1,5 |
10 |
9 |
3 |
2 |
2 |
0,12 |
0,18 |
0,1 |
2 |
15 |
10 |
1 |
1,5 |
!.7 |
0,1 |
0,15 |
0,22 |
1,6 |
12 |
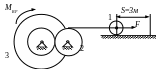
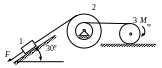
Схемы механизмов
1.
1
|
2 |
3
|
4 |
5
|
6 |
7
|
8 |
9
|
1 |
Схемы опор.
2
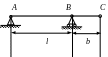
1 l=1,5м, b=0,5м, а=0,25м
В a
b
|
2
|
3 l=0,3м, b=1м, а=0,8м
|
4 l=1,5м, b=1м
|
5 l=2м
C
l
|
6 φ=60º
|
7
φ=60º
|
8 φ=60º
|
9
C
a
B
A
l
b
|
|
Пример. Применение принципа Даламбера (метода кинетостатики) для определения реакций связей
: m1=1,5кг, m2= 3кг, m3= 2кг, r=0,12м, R=0,24м, I=0,25кгм2, Р=25Н.

45º
45º
Рис.3.7 Схема механической системы.
Решение
Установим кинематические зависимости. Механизм имеет одну степень свободы, поэтому ускорения грузов зависят от углового ускорения блока. Обозначим ускорения грузов а1 и а2, а угловое ускорение блока ε. Тогда
а1= ε·r и а2= ε·R,
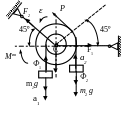
Рис.3.8 Силовая схема.
Изобразим
действующие на механическую систему
силы: внешние активные силы m1g,
m2g,
m3g;
реакции
внешних связей силы натяжения невесомых
стержней АС и ВС-![]() ;
силы инерции Даламбера для грузов 1 и
2, движущихся поступательно
;
силы инерции Даламбера для грузов 1 и
2, движущихся поступательно
![]() ,
а для тела 3 момент сил инерции
,
а для тела 3 момент сил инерции
![]() ,
здесь знак – указывает на то, что
направление момента противоположно
направлению углового ускорения. Блок
вращается вокруг неподвижной оси, в
этом случае силы инерции приводятся к
главному вектору
,
здесь знак – указывает на то, что
направление момента противоположно
направлению углового ускорения. Блок
вращается вокруг неподвижной оси, в
этом случае силы инерции приводятся к
главному вектору
![]() и к главному моменту сил инерции Mин.
Но так как
центр масс блока находится на неподвижной
оси в точке С, то
Ф3ин=0,
поэтому
учитываем только момент.
и к главному моменту сил инерции Mин.
Но так как
центр масс блока находится на неподвижной
оси в точке С, то
Ф3ин=0,
поэтому
учитываем только момент.
Согласно принципу Даламбера, который ещё называют методом кинетостатики, система перечисленных сил инерции, активных сил и сил реакций связей эквивалентна нулю. Составим для этих сил уравнения статики:
1)
![]() ;
F1-
F2cos45º-P
cos45º=0
;
F1-
F2cos45º-P
cos45º=0
2)
![]() ;
F2sin45º+P
sin45º+Ф1-Ф2-
m1g-
m2g-
m3g=0
;
F2sin45º+P
sin45º+Ф1-Ф2-
m1g-
m2g-
m3g=0
3)
![]() ;
Р·R-Мин+(m1g-Ф1)·r-(
m2g-Ф2)·R=0.
;
Р·R-Мин+(m1g-Ф1)·r-(
m2g-Ф2)·R=0.
Из последнего уравнения определим угловое ускорение ε. Для этого подставим в уравнение 3 значения сил инерции.
Р·R-I·ε+ m1g·r- m1·ε·r2- m2g·R- m2 ·ε·R2=0.
Отсюда
ε=![]() =
=![]() =0,9017с-2.
=0,9017с-2.
Из первых двух уравнений определяются реакции стержней F1 и F2,
F2=![]() ((m1+m2+m3)g-m1·ε·r+m2ε·R)-P=
93, 5Н,
((m1+m2+m3)g-m1·ε·r+m2ε·R)-P=
93, 5Н,
F1= (F2+P)·cos45º=83,79Н.
Ответ:F1=93,5 Н, F2=83,79 Н.























 0
0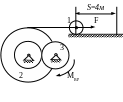

 2
2 4
4 5
5 6
6
 7
7 8
8
 0
0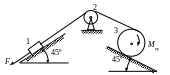 1
1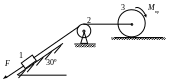 2
2 3
3 4
4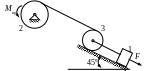

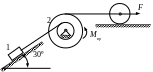 7
7
 8
8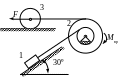 9
9









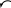
 1
1 2
2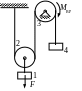 3
3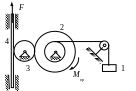 4
4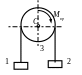





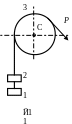

 0
0
 l=2м, b=1м,
φ=30º
l=2м, b=1м,
φ=30º


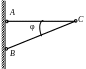 φ=30º
φ=30º











 0
l=2м, b=0,8м
0
l=2м, b=0,8м