дый атом (или молекула) поляризуют своего соседа, и он превращается в диполь,

вкотором заряды противоположных знаков пространственно разделены.

Умногих веществ, например у воды, молекулы при своем рождении сразу же оказываются подобными электрическому диполю. Такие молекулы своим электрическим полем вызывают поляризацию соседей и появление сил притяже-

ния. Силы Ван-дер-Ваальса - следствие некоторого преобладания притяжения над существующим одновременно отталкиванием, они резко убывают с увеличе-

нием расстояния (обратно пропорциональны седьмой степени расстояния!). Силы Ван-дер-Ваальса не способны объяснить образование молекул. При

сближении атомов начинают работать химические (обменные) силы, которые приводят к коллективизации внешних (валентных) электронов двух соединяющихся атомов. Эти электроны, проходя между ядрами, компенсируют их отталкивание и образуется устойчивое соединение (молекула).

Наличие химических и молекулярных сил позволяет объяснить и понять структуру газов, жидкостей и твердых тел и, в конечном итоге, их поведение под действием внешних сил.

2.1.3.УПРУГИЕ СИЛЫ

Вреальных газах и жидкостях из сил притяжения действуют только силы Ван-дер-Ваальса, а в твердых телах еще и обменные (химические) силы. Силы Ван-дер-Ваальса удерживают молекулы жидкости друг возле друга на близких расстояниях порядка размера самих молекул. Если попытаться жидкость сжать, то при сближении молекул между ними начнут быстро нарастать силы отталкивания. Вследствие того, что молекулы расположены очень тесно, уже при незначительном сближении силы отталкивания достигают очень большой величины.

Для упругих тел напряжения (силы, действующие на единичную площадь) прямо пропорциональны деформациям. Это закон Гука, который для жидкостей имеет вид:

p=-E V/V,

где p - сжимающее напряжение (гидростатическое давление), V - изменение объёма, а V - первоначальный объём.

Величину сил отталкивания и характеризует модуль объемной упруго-

сти E, который, например, для воды равен 2 109 Па. Нетрудно понять, что при сжатии твердых тел силы отталкивания еще больше (модуль объемной упругости для стали равен 2 1011 Па).

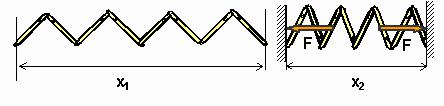
Упругие силы возникают в твердых телах не только при объемном, но и при линейном сжатии. Например, если поместить пружину в некое гнездо, предварительно уменьшив ее линейный размер на величину x, в ней возникает упругая си-

ла F.

F = k x, где x- предварительное поджатие пружины, x=x1-x2, а k - коэффициент жесткости, зависящий от материала пружи-

ны, ее размера и способа изготовления.

-12-