§ 4. Дифференцируемость функции нескольких переменных

1. Дифференцируемые функции нескольких переменных.

Пусть функция двух переменных определена в некоторой открытой областиплоскости,– точка области. Придавая переменным приращенияи, перейдем из точкив какую-нибудь точкутой же области. При этом функцияполучит приращение

.

В отличие от частных приращений иэто приращение называетсяполным приращениемфункциив точке, соответствующим приращенияминезависимых переменных.

ОПРЕДЕЛЕНИЕ. Функция называетсядифференцируемой в точке если ее полное приращение в этой точке может быть записано в виде

,(4.1)

где – некоторые числа,– бесконечно малые при,(или, короче при).

Замечание.Функцииизависят от.

Функция , дифференцируемая в каждой точке некоторой области, называетсядифференцируемой вэтойобласти.

Соотношение (4.1)можно записать и в более сжатой форме:

(4.2)

где ,– бесконечно малая при.

Слагаемое , линейное относительнои, являетсяглавной частью приращения, так как оставшееся слагаемое(или, если используется формула(4.2)) есть бесконечно малая более высокого порядка чеми.

ПРИМЕР. Функция будет дифференцируемой в любой точке, так как

Здесь – главная часть полного приращения функции, а слагаемоеесть бесконечно малая более высокого порядка по сравнению си.

Данное выше определение дифференцируемости функции двух переменных является естественным обобщением определения дифференцируемости функции одной переменной. Следовательно, можно поставить вопрос о том, какие из свойств дифференцируемых функций одной переменной сохранятся для функции двух переменных. Так, было установлено, что если функция одной переменной дифференцируема в некоторой точке, то она непрерывна и имеет производную в этой точке. Последнее условие оказалось и достаточным, т.е. из существования производной функции одной переменной в данной точке следует дифференцируемость функции в этой точке. На функции двух переменных эти свойства переносится в следующем виде.

ТЕОРЕМА 4.1. (необходимые условия дифференцируемости). Если функция дифференцируема в точке, то она непрерывна в этой точке и имеет в ней частные производные по обеим независимым переменным. Причем, а.

ДОКАЗАТЕЛЬСТВО…

1) Пусть дифференцируема в точке. Значит ее приращение в этой точке может быть записано в виде

, (*)

где – некоторые числа,– бесконечно малые при,. Тогда

.

С другой стороны,

.

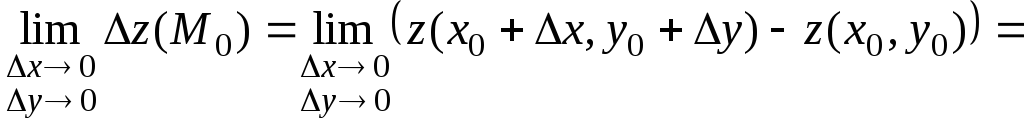
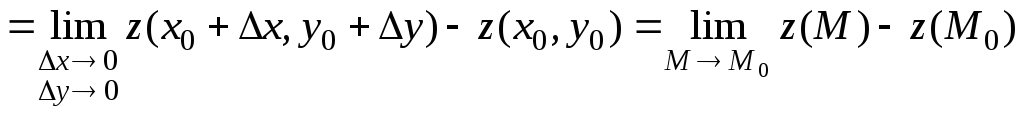Следовательно, ,

⇒ ,

т.е. непрерывна в точке.

2) Пусть . Тогда формула (*) примет вид

,

где – некоторое число,– бесконечно малая при,. Отсюда получаем:

и .

Аналогично доказывается, что существует .∎

С учетом теоремы 4.1равенства(4.1)и(4.2)можно теперь записать в виде(4.3)

(4.4)

где – бесконечно малые при,,,– бесконечно малая при.

Утверждение обратное теореме 4.1неверно. Из непрерывности функции двух переменных в точке и существования в этой точке ее частных производных еще не следует дифференцируемость функции.

ПРИМЕР. Функция непрерывна в точкеи имеет в этой точке частные производные:

,

.

Однако эта функция не является дифференцируемой в точке . Действительно, в этой точке ее полное приращение равно

.

Если бы функция была дифференцируемой в точке , то слагаемоеможно было бы представить в виде, где, а– бесконечно малая при. Но выделяя вмножитель, мы получаем второй множитель. А эта функция не является бесконечно малой при(при любыхимееми, значит, в любой сколь угодно малой окрестности точкивсегда найдутся точкидля которых неравенствоне выполняется для).

Для того, чтобы функция двух переменных была дифференцируема в данной точке, на нее, в отличие от функции одной переменной надо наложить боле жесткие требования, чем существование частных производных в этой точке. А именно, справедлива следующая теорема.

ТЕОРЕМА 4.2. (достаточные условия дифференцируемости). Если функция имеет в некоторой окрестности точкичастные производныеи, причем в самой точкеэти производные непрерывны, то функциядифференцируема в этой точке.

ПРИМЕР. 1) Функция в любой точкедифференцируема, так как ее частные производныеивсюду непрерывны.

2) Функция дифференцируема в каждой точке полуплоскости, так как там существуют и непрерывны ее частные производные.

И в заключение этого пункта заметим, что все определения и теоремы, которые мы здесь формулировали, легко переносятся на случай функций большего числа переменных.