
[ПС].Вышка.Шпоры.2семестр / шпоры_DOC / 07
.docкриволинейного интеграла I рода
Пусть
 – спрямляемая кривая в пространстве
– спрямляемая кривая в пространстве
 ,
вдоль которой распределена масса.
Определим массу кривой
,
вдоль которой распределена масса.
Определим массу кривой
 ,
если плотность распределения массы в
каждой точке
,
если плотность распределения массы в
каждой точке
 равна
равна
 .
.
Эту задачу можно решить следующим
образом. Разобьем кривую
 на
на
 дуг
дуг
 ,
,
 ,
…,
,
…,
 .
На каждой дуге
.
На каждой дуге
 выберем произвольную точку
выберем произвольную точку
 .
Если дуга
.
Если дуга
 мала, то можно считать ее однородной,
с плотностью распределения массы
мала, то можно считать ее однородной,
с плотностью распределения массы
 .
Тогда приближенное значение массы
.
Тогда приближенное значение массы
 дуги
дуги
 будет равно
будет равно
 ,
,
где
 – длина
– длина
 .
Так как масса
.
Так как масса
 всей кривой
всей кривой
 равна сумме масс ее частей, то
равна сумме масс ее частей, то
 .
.
Причем
разность
 будет тем меньше, чем мельче разбиение
кривой
будет тем меньше, чем мельче разбиение
кривой
 .
Следовательно, точное значение массы
кривой будет равно
.
Следовательно, точное значение массы
кривой будет равно  ,
(1)
,
(1)
где
 – наибольшая из длин
– наибольшая из длин
 .
.
К пределам вида (1) сводятся и ряд других задач математики и физики. Поэтому представляется целесообразным исследовать такие пределы, отвлекаясь от их конкретного содержания.
2. Определение и свойства криволинейного интеграла I рода
Пусть
 – спрямляемая кривая в пространстве
– спрямляемая кривая в пространстве
 и на кривой
и на кривой
 задана функция
задана функция
 .
.
1. Разобьем кривую
 произвольным образом на
произвольным образом на
 частей, не имеющих общих внутренних
точек:
частей, не имеющих общих внутренних
точек:
 ,
,
 ,
…,
,
…,
 .
.
2. На каждой дуге
 выберем произвольную точку
выберем произвольную точку
 и вычислим произведение
и вычислим произведение
 ,
где
,
где
 – длина дуги
– длина дуги
 .
.
Сумму
 назовем интегральной суммой
для функции
назовем интегральной суммой
для функции
 по кривой
по кривой
 (соответствующей данному разбиению
кривой
(соответствующей данному разбиению
кривой
 и данному выбору точек
и данному выбору точек
 ).
Очевидно, что интегральная сумма
).
Очевидно, что интегральная сумма
 зависит от способа разбиения кривой
зависит от способа разбиения кривой
 и выбора точек
и выбора точек
 и, следовательно, для функции
и, следовательно, для функции
 по кривой
по кривой
 можно записать множество различных
интегральных сумм.
можно записать множество различных
интегральных сумм.
Пусть
 – наибольшая из длин
– наибольшая из длин
 .
.
ОПРЕДЕЛЕНИЕ. Число
 называется пределом интегральных
сумм
называется пределом интегральных
сумм
 при
при
 (обозначают
(обозначают
 ),
если для любого
),
если для любого
 существует
существует
 такое, что для любого разбиения кривой
такое, что для любого разбиения кривой
 у которого
у которого
 ,
при любом выборе точек
,
при любом выборе точек
 выполняется неравенство
выполняется неравенство
 .
.
Если существует конечный предел
интегральных сумм
 при
при
 ,
то его называют криволинейным
интегралом I
рода (по длине дуги) от функции
,
то его называют криволинейным
интегралом I
рода (по длине дуги) от функции
 по кривой
по кривой
 .
.
Криволинейный интеграл I
рода от функции
 по кривой
по кривой
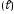 обозначают
обозначают

( называют подынтегральной функцией,
называют подынтегральной функцией,
 – областью интегрирования,
– областью интегрирования,
 – переменные интегрирования,
– переменные интегрирования,
 – дифференциал длины дуги).
– дифференциал длины дуги).
Если существует
 ,
то функция
,
то функция
 называется интегрируемой по кривой
называется интегрируемой по кривой
 .
.
Из определения следует, что криволинейный
интеграл I рода не зависит
от того, в каком направлении пробегается
кривая
 ,
т.е.
,
т.е.

 .
.
Достаточное условие существования криволинейного интеграла I рода будет сформулировано позже, когда покажем способ его вычисления.
Определение криволинейного интеграла I рода по структуре такое же, как и определение определенного интеграла. Поэтому криволинейный интеграл I рода обладает теми же свойствами, что и определенный интеграл. Приведем эти свойства без доказательства.
СВОЙСТВА КРИВОЛИНЕЙНОГО ИНТЕГРАЛА I РОДА
1.
 ,
где
,
где
 – длина кривой
– длина кривой
 .
.
2. Постоянный множитель можно выносить
за знак криволинейного интеграла I
рода, т.е.  .
.
3. Криволинейный интеграла I рода от алгебраической суммы двух (конечного числа) функций равен алгебраической сумме криволинейных интегралов I рода от этих функций, т.е.


 .
.
4. Если кривая
 разбита на две части
разбита на две части
 и
и
 ,
не имеющие общих внутренних точек, то
,
не имеющие общих внутренних точек, то



(свойство аддитивности криволинейного интеграла I рода).
5. Если всюду на кривой
 функция
функция

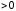 (
(
 ),
то
),
то

 .
.
6. Если всюду на кривой


 (
(
 ),
то
),
то 
 .
.
7. (следствие свойств 6 и 1) Если
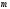 и
и
 – соответственно наименьшее и наибольшее
значения функции
– соответственно наименьшее и наибольшее
значения функции
 на кривой
на кривой
 ,
то
,
то


 ,
,
где
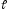 – длина кривой
– длина кривой
 .
.
8. (теорема о среднем для криволинейного
интеграла I рода) Если
функция
 непрерывна на кривой
непрерывна на кривой
 1,
то найдется такая точка
1,
то найдется такая точка

 ,
что справедливо равенство
,
что справедливо равенство

 ,
,
где
 – длина кривой
– длина кривой
 .
.
3. Вычисление криволинейного интеграла I рода
Пусть кривая
 задана параметрическими уравнениями:
задана параметрическими уравнениями:
 ,
,
 ,
,
 (где
(где
 ). (2)
). (2)
Если функции
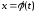 ,
,
 ,
,
 имеют на
имеют на
 непрерывные производные, которые не
обращаются в нуль одновременно, то
кривая
непрерывные производные, которые не
обращаются в нуль одновременно, то
кривая
 называется гладкой.
называется гладкой.
Если функции
 ,
,
 ,
,
 имеют на
имеют на
 кусочно-непрерывные производные,
которые не обращаются в нуль одновременно,
за исключением конечного числа точек,
то кривая
кусочно-непрерывные производные,
которые не обращаются в нуль одновременно,
за исключением конечного числа точек,
то кривая
 называется кусочно-гладкой.
называется кусочно-гладкой.
Справедлива следующая теорема.
ТЕОРЕМА 1. Если
 – гладкая кривая, заданная уравнениями
(2) и функция
– гладкая кривая, заданная уравнениями
(2) и функция
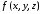 непрерывна на
непрерывна на
 ,
то
,
то
 интегрируема по кривой
интегрируема по кривой
 и справедливо равенство
и справедливо равенство
 . (3)
. (3)
ДОКАЗАТЕЛЬСТВО
По определению


 .
.
Так
как
 ,
то
,
то
 такое, что
такое, что
 ,
,
 ,
,
 .
.
Следовательно,

 .
.
Найдем
 .
Пусть
.
Пусть
 ,
,
 – начало и конец дуги
– начало и конец дуги
 .
Если
.
Если
 мала, то можно предполагать, что
мала, то можно предполагать, что

 .
.
⇒

 .
.
Но
 ,
,
 .
.
Следовательно,  .
.
Аналогично  и
и
 .
.
Таким образом,


 . (4)
. (4)
(Считаем,
что
 .
Такое предположение допустимо, поскольку
в противном случае будем считать
.
Такое предположение допустимо, поскольку
в противном случае будем считать

 ,
а для отрезка
,
а для отрезка
 тогда получим
тогда получим
 ).
).
Итак, получили:


 .
.
Пусть
 .
По условию кривая
.
По условию кривая
 – гладкая. Значит функции
– гладкая. Значит функции
 ,
,
 ,
,
 на
на
 непрерывны и в силу (4)
непрерывны и в силу (4)
 при
при
 .
Следовательно,
.
Следовательно,

 .
.
 .
∎
.
∎
НАПРИМЕР. Найти интеграл
 ,
где
,
где
 – один виток винтовой линии
– один виток винтовой линии
 ,
,
 ,
,
 (
( ).
).
Имеем:  ,
,
 ,
,
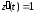 .
.
Следовательно,


 .
.
СЛЕДСТВИЕ 2. Если
 – гладкая кривая в плоскости
– гладкая кривая в плоскости
 ,
заданная уравнением
,
заданная уравнением
 (где
(где
 )
и функция
)
и функция
 непрерывна на
непрерывна на
 ,
то
,
то
 интегрируема по кривой
интегрируема по кривой
 и справедливо равенство
и справедливо равенство
 .
.
ДОКАЗАТЕЛЬСТВО
Пусть
 .
Тогда
.
Тогда
 ,
,
 (
( )
– параметрические уравнения кривой
)
– параметрические уравнения кривой
 .
Следовательно, по формуле (3)
.
Следовательно, по формуле (3)

 .
∎
.
∎
СЛЕДСТВИЕ 3. Пусть
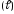 – плоская кривая, заданная в полярных
координатах уравнением
– плоская кривая, заданная в полярных
координатах уравнением
 (где
(где
 ).
Если функция
).
Если функция
 непрерывно дифференцируема на
непрерывно дифференцируема на
 и функция
и функция
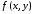 непрерывна на
непрерывна на
 ,
то
,
то
 интегрируема по кривой
интегрируема по кривой
 и справедливо равенство
и справедливо равенство
 .
.
ДОКАЗАТЕЛЬСТВО – самостоятельно
Подсказка: записать параметрические
уравнения кривой, используя формулы
перехода от полярных координат к
декартовым и считая
 – параметром.
– параметром.
В заключение этого пункта сформулируем теорему, которая очевидным образом следует из теорем 1 – 3.
4. Геометрические и физические приложения
криволинейных интегралов I рода
-
Длина
 спрямляемой кривой
спрямляемой кривой
 может быть найдена по формуле
может быть найдена по формуле
 .
.
-
Пусть
 – цилиндрическая поверхность, образующей
которой является кривая
– цилиндрическая поверхность, образующей
которой является кривая
 .
Тогда площадь
.
Тогда площадь
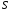 части поверхности
части поверхности
 ,
заключенной между плоскостью
,
заключенной между плоскостью
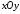 и поверхностью
и поверхностью
 ,
может быть найдена по формуле
,
может быть найдена по формуле
 .
.
(доказательство – самостоятельно)
Пусть
 – материальная спрямляемая кривая в
пространстве
– материальная спрямляемая кривая в
пространстве
 с плотностью
с плотностью
 .
Тогда справедливы следующие формулы:
.
Тогда справедливы следующие формулы:
-
 – масса кривой
– масса кривой
 .
. -
Статические моменты кривой
 относительно плоскостей
относительно плоскостей
 ,
,
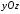 и
и
 равны соответственно:
равны соответственно:
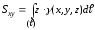 ,
,
 ,
,
 .
.
-
 ,
,
 ,
,
 – координаты центра тяжести кривой
– координаты центра тяжести кривой
 .
. -
Моменты инерции кривой
 относительно осей
относительно осей
 ,
,
 и
и
 равны соответственно:
равны соответственно:
 ,
,
 ,
,
 .
.
-

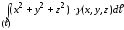 – момент инерции кривой
– момент инерции кривой
 относительно начала координат.
относительно начала координат.
1 Функция называется непрерывной на кривой , если выполняется условие . Если это условие выполнено в каждой точке кривой, за исключением конечного числа точек, в которых функция имеет разрывы I рода, то функция называется кусочно-непрерывной на кривой .
