З аняття № 62 Тема: Гіпотези міцності та їх застосування. План

1. Призначення гіпотез міцності. Еквівалентні напруження. П’ять гіпотез міцності та їх сутність.

Студент повинен знати: сутність гіпотез міцності, методи визначення еквівалентних напружень.

Студент повинен вміти: визначати вид деформації та вид напруженого стану.

ЛІТЕРАТУРА ОСНОВНА

ЛІТЕРАТУРА ДОДАТКОВА

При першому знайомстві з механічними напруженнями відмічалося, що напруження в точці залежать від орієнтації перерізу. Сукупність напружень, що діють по різних площадках, проведених через точку, характеризують напружений стан у точці.

Оберемо довільну ортогональну систему координат і запишемо напру­ження, які діють у досліджуваній точці деталі на малих координат­них площадках (рисунок 1 а), у вигляді

(1)

Математичний об’єкт (1) називають тензором напружень .

Рисунок 1

У тій самій точці деталі уявно виріжемо тетраедр (рисунок 1 б), три грані якого – координатні площадки, а одна грань – довільно орієнтована площа­дка з нормаллю . Якщо заданий тензор , тобто задані напруження на ко­ординатних площадках, то з трьох рівнянь рівноваги ( , , ) сил, що діють на грані тетраедра, можна визначити три невідомі скла­дові повного напруження на довільній площадці. Оскі­льки таким чином можна визначити напруження на будь-якій площадці, то можна стверджувати:

Тензор напружень цілком визначає напружений стан у точці.

Тензор напружень симетричний відносно головної діагоналі:

; ; . (2)

Це можна довести з рівнянь рівноваги ( , , ) щодо моментів сил, які діють на грані малого кубика (рис. 1 а). Рівняння (2) відомі як закон парності дотичних напружень:

На будь-яких ортогональних площадках дотичні напруження,

перпендикулярні спільному ребру цих площадок, рівні за величиною

та спрямовані обидва до ребра або обидва від ребра.

Тензор напружень може бути приведений до діагонального виду

( ) (3)

Ц е означає, що у будь-якій точці деталі завжди знайдуться три ортогональні головні площадки, на яких немає дотичних напружень. Ці площадки розташовуються у площинах симетрії еліпсоїда, в який перетворюється кулька після деформування (рисунок 2).

Нормальні напруження на головних площадках називаються головними напруженнями.

Їм дають числові індекси відповідно з правилом

Головні напруження являються коренями характеристичного або, за іншою назвою, „вікового” рівняння тензора напружень:

. (4)

Головні напруження мають екстремальні властивості, тобто – найбільше, а – найменше за інші напруження на будь-яких площадках в даній точці деталі.

„Вікове” рівняння (4) завжди має три дійсні корені – головні напруження. Відповідно до кількості ненульових коренів класифікують види напруженого стану (НС):

• Одновісний (лінійний) НС – лише одне головне напруження ненульове.

• Двовісний (плоский) НС – два з трьох головних напружень ненульові.

• Т рьохвісний (об’ємний) НС – всі три головні напруження ненульові.

Особливо можна виділити окремий випадок двохвісного НС – чистий зсув:

М ожна довести, що на площадках, однаково нахилених до головних площадок та (тобто під кутом ), діють максимальні дотичні напруження, величина яких

(5)

Ці дотичні напруження більші за всі , які діють на будь-яких інших площадках у даній точці деталі. Як ми узнаємо далі, на цьому важливому факті будується один з підходів щодо оцінки небезпечності напруженого стану в точці.

У загальному випадку всякому напруженому стану в точці деталі відповідає певний деформований стан, який представляє сукупність лінійних деформацій по різних напрямках та кутових деформацій на всіляко орієнтованих площадках. Аналогічно тензору напружень тензор деформацій (6)

цілком визначає деформований стан у точці. Тензор деформацій має властивості, аналогічні властивостям тензора напружень . Головні деформації – це деформації у напрямках головних напружень .

Зв’язок між компонентами і встановлюють експериментально та формулюють у виді фізичного закону. Для пружного матеріалу при малих деформаціях напруження і деформації зв’язані лінійними залежностями, які називають узагальненим законом Гука (всього шість рівнянь (7), (8)):

; ;

; (8.7) ; (8)

; ,

де , , – пружні константи.

Наведені вище математичні залежності використовуються в уточнених розрахунках на міцність деталей при складному опорі. Разом з тим в інженерній практиці досить широке розповсюдження отримали розрахунки на міцність з використанням відповідних теорій міцності.

В багатьох елементах конструкцій, які мають складну геометричну форму або піддаються складному навантаженню, аналіз виявляє складний (2- або 3-вісний) напружений стан (НС) у певних точках цих конструкцій. У таких випадках виникають дві пов’язані проблеми:

П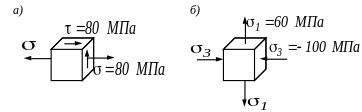 о-перше, за якою мірою (критерієм) порівнювати напружені стани? Наприклад, який НС, серед наведених на рисунку 8.3, найбільш небезпечний?

Рисунок 3

По-друге, як при зростанні навантаження прогнозувати граничний напружений стан, наприклад, початок пластичного деформування або початок крихкого руйнування? Це проблема оцінки коефіцієнта запасу при складному НС.

Легко звести ці дві проблеми до однієї за допомогою поняття про еквівалентне напруження:

– це таке напруження простого розтягу, яке за обраним

критерієм є рівнонебезпечним даному складному напруженому стану.

Маючи правило підрахунку , з двох складних НС будемо вважати більш небезпечним той, для якого більша величина , а граничним будемо вважати такий НС, для якого або . Умова міцності запишеться у виді .

Розглянемо лише кілька найбільш розповсюджених у практиці інженерних розрахунків критеріїв, за допомогою яких вирішуються поставлені проблеми.

Критерій максимальних дотичних напружень (Треска – Сен-Венана)

(ІІІ-й за історичною нумерацією у підручниках і довідниках)

Згідно з цим критерієм вважають: Граничний стан настає тоді, коли максимальні дотичні напруження (8.5) сягають характерного для даного матеріалу значення . Відповідно, більш небезпечною буде та точка деталі, де найбільше значення має .

Якщо застосувати формулу (5) для заданого складного НС та еквівалентного йому за величиною простого розтягу, то отримаємо таку формулу для еквівалентного напруження:

(9)

Застосуємо цей критерій для НС на рисунку 3 а. Такий тип двохвісного НС часто зустрічається в задачах на сумісну дію згину та кручення. Головні напруження знаходяться з «вікового» рівняння (4). Після їх підстановки у (9) отримаємо

(10)

У прикладі на рисунку 3 підрахунки дають ; , тобто перший НС більш небезпечний.

Критерій питомої потенційної енергії формозміни (Губера – Мізеса)

(ІV-й за історичною нумерацією у підручниках і довідниках)

Пояснимо деякі слова у назві критерію. „Питома” енергія означає, що енергія розраховується на одиницю об’єму. Потенційна енергія, накопичена у деформованій деталі, умовно розбивається на дві частини: одна пов’язана зі зміною об’єму, інша – тільки зі зміною форми. Енергія зміни об’єму виключається з розгляду, а за критерій береться лише питома потенційна енергія формозміни .

Згідно з IV критерієм вважають: Граничний стан настає тоді, коли питома потенційна енергія формозміни сягає характерного для даного матеріалу значення . Відповідно, більш небезпечною буде та точка деталі, де найбільше значення має .

Еквівалентне напруження за цим критерієм визначається формулою

. (11)

Застосуємо цей критерій для НС на рисунку 8.3 а. Знайшовши головні напруження з „вікового” рівняння (4), отримаємо після їх підстановки у (11) та значних спрощень

. (12)

У прикладі на рисунку 3 підрахунки дають

; ,

тобто і за цим критерієм перший НС більш небезпечний.

Відмітимо, що ІІІ і ІV критерії дають близькі результати, різниця не перевищує . Обидва критерії непогано підтверджуються випробуваннями для матеріалів, які однаково опираються розтягу і стиску. Появу у матеріалі малих пластичних деформацій ІV критерій визначає більш точно ніж ІІІ.

Для крихких матеріалів, для яких границя міцності на розтяг зазвичай набагато менша, ніж на стиск , ІІІ і ІV критерії непридатні.

Критерій Мора (феноменологічний підхід)

В інженерній практиці широкого розповсюдження набув критерій Мора, який будується на експериментальних даних без будь якої фізичної гіпотези. Слово „феноменологічний” саме і означає, що не наводиться фізичного тлумачення запропонованої формули, аби вона підтверджувалася випробуваннями. Згідно з цим критерієм умова міцності має вид

, (13)

де і – відповідно граничне і допустиме напруження на розтяг;

– граничне напруження на стиск.

Питання для самоконтролю

1. Дати визначення лінійного, плоского і об'ємного напружених станів. Навести приклади.

2. Які правила знаків вводяться для нормальних і дотичних напруг?

3. Доведіть, що сума нормальних напруг на двох довільних взаємно перпендикулярних площадках, що проходять через дану точку навантаже­ного тіла, величина стала.

4. Що таке головні площини і головні напруги?

5. Що таке октаедричні нормальна і дотична напруги та інтенсив­ність напруг? Для чого ці величини використовують в опорі матеріалів?

6. Що розуміють під небезпечним станом навантаженого тіла? Яка точка перерізу тіла називається небезпечною?

7. Що розуміють під гіпотезами міцності? Перелічіть відомі вам теорії міцності.

8. Сутність і область використання третьої теорії міцності? На­пишіть умову міцності за третьою теорією.

9. Сутність і область використання четвертої теорії міцності? Напиліть умову міцності за четвертою теорією.

Заняття № 63

Тема: Гіпотези міцності та їх застосування.

План

1. Складний згин. Косий згин

2. Розрахунки брусу круглого поперечного перерізу при одночасній дії згину і кручення при загальному випадку навантаження.

Студент повинен знати: Формули для визначення прогину і кутів обертання поперечних перерізів.

Студент повинен вміти: розрахунки на жорсткість при прямому згині.

ЛІТЕРАТУРА ОСНОВНА

ЛІТЕРАТУРА ДОДАТКОВА

1. Складний згин. Косий згин

Складним згином називають випадок, коли балку навантажують у різних площинах,

які, проходячи через центральну вісь, не співпадають з головними площинами інерції.

Частковий випадок складного згину – це косий згин – випадок складного, коли

навантаження прикладають в одній площині, яка, проходячи через центральну вісь, не

співпадає з жодною із головних площин інерції.

Визначення напружень при косому згині. Умова міцності.

Розглянемо, наприклад, консольну балку (рис.1а), навантажену на вільному кінці

силою, лінія дії якої, проходячи через центр ваги перерізу (для визначеності виберемо його

прямокутним), відхиляється від вертикальної головної осі на кут φ (рис.1б).

Рис.1. Косий згин: а) − загальний вид навантаження;

б) − орієнтація навантаження в перерізі

Для з΄ясування, з якими простими деформаціями маємо справу, розглянемо рис. 2.

Розклавши силу F на горизонтальну Fгор та вертикальну Fверт складові, запишемо

Тепер неважко помітити, що сила Fгор викликає згин у горизонтальній площині, а

сила Fверт − відповідно згин у вертикальній площині. Згинальні моменти відповідно

Від цих обох згинів у площині перерізу виникають нормальні напруження і тому їх

можна просто алгебраїчно скласти. В силу того, що в більшості випадків дотичні

напруження не відіграють суттєвої ролі, при розгляді косого згину ми їх розглядати не

будемо. І тоді

а бо, перетворюючи

 (1)

Зауважимо, що ця формула записана для балки, що

розглядається у вибраній нами системі координат

і не носить узагальненого змісту.

На рис. 3 зображено епюри напружень У Fгор

у перерізі балки „а” – при прямому згині і „б” −

при косому.

Рис.2. Складові сили в перерізі

Для того, щоб знайти точки, в яких виникатимуть найбільші напруження, треба визначити положення нейтральної осі. Для цього прирівняємо вираз нормальних напружень до нуля .

Рис. 3. Епюри розподілу напружень у перерізі:

а) − при прямому згині, б) − при косому згині

У зв΄язку з тим, що добуток F·x не дорівнює нулю, прирівняємо до нуля тільки вираз у

дужках

(2)

де координати точок нейтральної осі.

Розглядаючи вираз, бачимо, що:

- нейтральна вісь дійсно є прямою лінією, між координатами спостерігається

лінійна залежність;

- нейтральна вісь проходить через центр ваги перерізу, якщо у₀=0, то і z₀=0;

- нейтральна вісь розвертається на певний кут α відносно горизонтальної головної

осі інерції (рис.4):

або (3)

Рис.4. Положення нейтральної осі при косому згині

З формули (3) випливає, що чим більшою є різниця між головними осьовими

моментами інерції, тим більшою вона буде між кутом відхилення нейтральної осі та кутом відхилення площини, в якій діють навантаження, від головної площини інерції − тобто, можливі випадки, за яких . З точки зору інженерної практики − це означає, що невеликі кутові зміщення площини дії сил можуть призвести до значних

відхилень площини деформацій. н.в. А В. З даного співвідношення бачимо: α,якщо головні моменти інерції однакові (у випадку кола та правильних многокутників), косого згину не відбувається.

Тепер, коли з΄ясовано положення нейтральної осі, стає очевидним положення точок В і Д, в яких виникатимуть Д Снайбільші розтягуючі та стискаючі нормальні напруження (рис.10.4).

Якщо конструкція виготовлена з пластичного матеріалу, для якого будуть однаковими рівні допустимих напружень на розтяг [σ_р] та стиск [σ_cт], то умову міцності можна записати

Або

(4)

З цієї умови, як і у випадку прямого згину, знаючи розміри поперечного перерізу,

можна визначити допустимі сили, або, знаючи їх, визначити розміри поперечного перерізу.

Слід зауважити, що для визначення цих розмірів слід наперед задати їх співвідношення , тому що з однієї нерівності не можна однозначно визначити два невідомих.

Сумісна дія згину та кручення.

Круглі вали. Сили, що діють на вали (тиск на зуби шестірень, натяг ременів, власна вага вала й шківів і т.п.), викликають у поперечних перерізах валів наступні внутрішні силові фактори:  ;  ;  ;   і  . Таким чином, у будь-якому поперечному перерізі одночасно виникають нормальні напруження;tyyz від вигину у двох площинах, а також дотичні напруження від крутіння й вигину.

Для розрахунку вала в першу чергу необхідно встановити небезпечні перерізи. Із цією метою повинні бути побудовані епюри згинальних моментів  ,   і крутного моменту  .

Навантаження, що діють на вал, розкладаємо на складові уздовж координатних осей (рис. 10.29), а потім будуємо епюри: від сил   - епюру  , від сил   -епюру   (рис.5, б и в).

А
Б
В
Г
д

Рис. 5. Вигин із крутінням вала

При вигині вала круглого або кільцевого перетину в кожному з його перетинів має місце прямий вигин під дією результуючого згинального моменту

(4)

Вектор моменту М у різних перетинах може мати різні напрямки, у силу чого навіть при відсутності розподілених навантажень епюра М може бути криволінійною (рис. 5, г). Для загального випадку це легко показати аналітично.

Нехай   (a, b, з, d — постійні коефіцієнти). Тоді

Вираз, що стоїть під радикалом, лише в деяких окремих випадках є повним квадратом (наприклад, при  ), а в більшості випадків епюра криволінійна, причому

Це дозволяє будувати епюри М спрощеним способом, трохи завищуючи значення сумарного згинального моменту М на ділянках між переломами епюри: величини сумарного згинального моменту М обчислюють лише для тих перетинів, у яких на епюрах   і   є переломи. Ці величини відкладають у масштабі по одну сторону від осі на епюрі М и з'єднують прямою лінією.

Далі будуємо епюру   (рис. 5, д) і шукаємо небезпечні перерізи, у яких одночасно великі M і  . Зіставляючи епюри, знаходимо, що небезпечним буде перетин 1 — 1 або 2 — 2.

Тепер у небезпечному перерізі потрібно знайти небезпечні точки. Визначаємо положення нейтральної лінії   і будуємо епюру нормальних напружень   від результуючого згинального моменту М (рис. 6), які змінюються пропорційно відстані точок від нейтральної лінії. Очевидно, небезпечними є точки A і В, найбільш вилучені від нейтральної лінії, — у них одночасно і нормальні напруження від вигину і дотичні напруження мають найбільші значення:

	(5)
	(6)

Рис. 6. Епюра нормальних напружень

У найнебезпечнішої точки У виділимо елемент (рис. 7) По чотирьох його гранях діють дотичні напруження, а до двох із цих граней прикладені ще й нормальні напруження. Інші дві грані вільні від напружень. Таким чином, при вигині із крутінням елемент у небезпечній точці перебуває в плоскому напруженому стані.

Рис. 7. Елемент вала при вигині із крутінням

Зовсім аналогічними були напруження на гранях у брусі який згинається, тому тут головні напруження потрібно визначати по тим же формулам:

(7)

Різниця між виразами (6) і (7) лише в тім, що в останньому випадку дотичні напруження викликаються крутним моментом, а при вигині вони викликалися поперечною силою.

Помітимо, що в цьому випадку складного напруженого стану впливом дотичних напружень від поперечних сил зневажаємо, тому що вони значно менше дотичних напружень, викликаних крутінням.

Для перевірки міцності елемента, виділеного в небезпечної точці потрібно, вибравши відповідну теорію міцності:

по теорії Мору

(8)

по IV теорії

(9)

Підставляючи у формули (8), (9) вираз для напружень і з огляду на, що  , одержимо

	(10)
	(11)

Чисельники цих формул являють собою наведені моменти, дія яких еквівалентно спільній дії трьох моментів (відповідно до прийнятої теорії міцності). Отже,

	(12)
	(13)

Якщо буде потреба подібним же чином можна одержати формули для наведених моментів і по інших теоріях  міцності.

Неважко помітити, що тепер умови міцності можна замінити однією простою формулою

(14)

Таким чином, при спільній дії вигину із крутінням стрижні круглого перетину розраховують на вигин від приведеного моменту М_пр.

Вирішуючи нерівність (14) відносно W, одержуємо формулу для визначення моменту опору:

(15)

і діаметра круглого вала:

(16)

Помітимо, що наведені формули повністю застосовні і до стрижнів кільцевого перетину.

Розглянемо найпростіший приклад розрахунку вала на вигин із крутінням.

Приклад 1. На вал (рис. 8) насаджені три зубчасті колеса. Колеса навантажені силами  ;  ;  , причому сила   вертикальна, а сили   й   горизонтальні. Діаметри зубчастих коліс наступні:  ;  ;  .  Допустиме напруження . Підібрати діаметр вала по четвертій теорії міцності.

Рис. 8. До прикладу 1

Замінимо навантаження статично еквівалентною системою сил.

Перенесемо сили  ,   і   на вісь вала, заміняючи кожну з них силою, прикладеної в точці В, З або D відповідно, і парою, що скручує,   сил  ;   ; відповідно. Таким чином, одержуємо розрахункову схему (рис. 10.32). На схемі зазначені як значення прикладених зовнішніх навантажень  , так і величини викликаних ними опорних реакцій.

Розглядаючи окремо сили в горизонтальній і вертикальній площинах (рис.9, а й б), будуємо епюри згинальних моментів. Для побудови сумарної епюри моментів М обчислюємо ординати в характерних точках по формулі :

у перетині В

у перетині C

у перетині D

а
б
в
г

Рис. 9. Побудова епюр до прикладу 1

Епюра М, побудована за цим даними, наведена на рис. 9, в. Як вказувалося раніше, на ділянках ВР і CD такаючи епюра має завищені значення ординат (дійсні значення показані штриховою лінією).

Розглядаючи діючі на вал моменти, будуємо епюру крутних моментів (рис. 9, г).

Зіставляючи епюри M і  , знаходимо, що небезпечним є перетин 1 – 1, розташований ліворуч від точки С, де одночасно діють   і  .

Згідно IV теорії міцності, наведений момент обчислимо по формулі (13). Одержимо

Підставляючи наведений момент у формулу (15), знаходимо необхідний осьовий момент опору:

і, поклавши  , обчислюємо необхідний діаметр вала:

Округливши до найближчого стандартного діаметра, приймаємо  .

Брус прямокутного перетину. На практиці часто зустрічаються стрижні некруглого перетину, піддані дії крутних і згинальних моментів. Як приклад розглянемо брус прямокутного перетину (рис. 10, а), навантажений силами   й  , що викликають у поперечних перерізах згинальні моменти   й  , а також поперечні сили   й  .

а
б

Рис. 10. Брус прямокутного перетину

Розрахунок виконуємо в такій послідовності. Розкладаємо задані навантаження (сили   й  ) на складові уздовж координатних осей і приводимо їх до осі вала; при цьому одержуємо в поперечних перерізах, у площинах яких перебувають точки прикладання сил, зовнішні моменти, що скручують,   і  . Отримана в такий спосіб розрахункова схема представлена на рис. 10.

Для того щоб установити положення небезпечного переріза, будуємо епюри згинальних моментів   і  , а також епюру крутних моментів   (рис. 10, б).

Зіставлення епюр показує, що найнебезпечнішим є перетин 1 — 1 бруса, розташований ліворуч точки прикладання сили  . У цьому перетині діють найбільші згинальні моменти  ,   і максимальний крутний момент  . Щоб перевірити міцність бруса, потрібно в небезпечному перерізі знайти небезпечну точку, обчислити для неї еквівалентне напруження (по одній з теорій міцності) і зіставити його з допустимим напруженням, що.

Для знаходження небезпечної точки перетину будуємо епюри напружень від всіх силових факторів (рис. 11, б-е):  ;  ;  ;  ;  .

Епюра   для довгої сторони контуру має максимум, що позначимо  . Найбільшу ординату епюри   на короткій стороні позначимо  . Ці напруження можна розрахувати по відомих формулах крутіння брусів прямокутного перетину:

(17)

Епюри нормальних і дотичних напружень наочно показують, що на відміну від круглого перетину в розглянутому випадку найбільші нормальні напруги   й найбільші дотичні напруження   й   мають місце не в одній і тій же точці.

а	б	в
г	д	е

Рис. 12. Епюри напружень

Отже, для виявлення самої небезпечної точки в перетині; потрібно зіставити еквівалентні напруження в декількох небезпечних точках. Звичайно вважають достатнім розглянути три точки перетину: одну кутову точку (A або С), одну точку посередині довгої сторони прямокутника (L або Т) і одну точку посередині короткої сторони прямокутника (S або K).

Елемент, виділений в околиці точки С (при прийнятих на рис. 12, а напрямках М_у й M_z), перебуває в умовах простого розтягання напруженнями, рівними сумі нормальних напружень від М_у й M_z. Тому умова міцності для цієї точки повинна бути записана як для випадку лінійного напруженого стану:

(18)

Елемент в околиці точки А також перебуває в умовах лінійного напруженого стану — простого стиску, тому що   відрізняється від   тільки знаком. Якщо матеріал бруса має різні допустимі напруження, що, для розтягання й для стиску, то перевіряти міцність по формулі (18) необхідно в кожній із цих точок.

Елементи в околиці точок L і K перебувають у плоскому напруженому стані, і, отже, головні напруження в них, як і в круглому брусі, можна обчислити по формулі (7). У загальному випадку дотичні напруження, що входять у формулу (7), варто обчислювати як від дії крутного моменту , так і від дії поперечних сил:

(19)

Однак дотичні напруження від поперечних сил Q_y і Q_z, як відзначалося, звичайно мале, а тому в більшості випадків їх впливом можна зневажити.

Для обчислення еквівалентних напружень у точках L і K підставляємо значення нормальних і дотичних напружень у формули (8) і (9). Одночасно одержимо і відповідні умови міцності (по IV теорії й по теорії Мору):

у точці L

	(20)
	(21)

у точці K

	(22)
	(23)

Знаки моментів при підстановці їх у рівняння (20) – (23) не мають значення, тому що в ці формули входять квадрати моментів.

Таким чином, найнебезпечніша точка визначається тільки в результаті обчислення еквівалентних напружень у всіх трьох точках (З, L і K) по формулах (18) і (20) — (23), причому в кожному окремому випадку положення найнебезпечнішої точки залежить від конкретного співвідношення величин моментів  ,   і  . 

Питання для самоконтролю

1. Дайте визначення косого згину.

2. Напишіть формулу для визначення нормальних напруг у попереч­ному перерізі бруса при косому згині.

3. Як визначити положення нейтральної лінії при косому згині?

4. Як визначити положення нейтральної лінії при позацентровому розтягу /стиску/?

5. Як визначити небезпечний переріз вала при згині з крученням? Який напружений стан виникає в поперечному перерізі?

6. Розкрийте, сутність проектного і перевірного розрахунків на міцність вала при згині з крученням.