
- •Модуль 12 Елементи теорії ймовірностей та математичної статистики зм 34 Елементи комбінаторики
- •Опорні питання заняття:
- •Запитання для самоперевірки
- •Опорні питання заняття:
- •Множини. Операції над множинами
- •Операції над множинами
- •Виконання вправ
- •Виконання вправ
- •Різницею множин а і в називається множина всіх таких елементів множини а, які не містяться у множині в.
- •Перестановки
- •Розміщення
- •Комбінації. Трикутник Паскаля
- •Розв'язання
- •Розв'язання
- •Біном Ньютона
- •Розв'язання
- •Розв'язання
- •Розв'язання
- •Розв'язування прикладних задач
- •Розв'язання
- •Запитання для самоперевірки
Розв'язання
а) Хлопчика можна вибрати 12 способами, а дівчинку — 10 способами, тоді за правилом суми або дівчинку, або хлопчика можна вибрати 12 + 10 = 22 (способами).
б) Хлопчика можна вибрати 12 способами, а дівчинку — 10 способами, тоді за правилом добутку і дівчинку, і хлопчика можна вибрати 12 · 10 = 120 (способами).
в) Дівчинку можна вибрати 10 способами.
г) Якщо один учень уже вибраний, то можливі два варіанти:
1) якщо був вибраний хлопчик, то хлопчиків залишилося 11, отже існує 11 варіантів його вибору, для дівчинки — 10 варіантів, для пари 11 · 10 = 110 (варіантів).
2) Якщо була обрана дівчинка, тоді дівчаток залишилося 9, отже дівчинку вибрати можна 9 способами, хлопчика — 12 способами, а пару можна вибрати 9 · 12 = 108 (способами), За правилом суми маємо загальну кількість варіантів 11 · 10 + 12 · 9 = 110 + 108 = 218.
Відповіді: а) 22; 6)120; в) 10; г) 218.
Виконання вправ
7 книг різних авторів і трьохтомник одного автора розташовані на книжковій полиці. Скількома способами можна розставити ці 10 книжок на полиці так, щоб книги автора трьохтомника стояли поруч?
Відповідь: P3 · P8 = 241 920.
Збори з 30 осіб обирають голову, секретаря та трьох членів редакційної комісії. Скількома способами це можна зробити?
Відповідь:
 ·
= 2 850 120.
·
= 2 850 120.
У підрозділі 60 солдат і 5 офіцерів. Скількома способами можна виділити наряд, який складається із трьох солдат і одного офіцера?
Відповідь: · = 171100.
Із 10 троянд і 8 жоржин треба скласти букет так, щоб в ньому були 2 троянди і 3 жоржини. Скількома способами можна скласти букет?
Відповідь: · = 2520.
Із семи бігунів і трьох стрибунів треба скласти команду із 5 чоловік, в яку б входив хоч би один стрибун. Скількома способами це можна зробити?
Відповідь: + + = 231.
Запитання для самоперевірки
Дайте визначення множині.
Як позначається множина та її елементи?
Які способи задання множин Ви знаєте?
Що називають скінченною множиною, нескінченною множиною? порожньою множиною?
Що називають підмножиною деякої множини? Як це можна ілюструвати? Як це записати символічно?
Які дії над множинами Ви знаєте? Дайте характеристику кожній дії (сума, різниця, переріз множин)
Які числові множини Ви знаєте? Як вони між собою пов’язані?
Що називають упорядкованою множиною?
Що таке перестановки? Поясніть формулу.
Що таке розміщення? Яка його формула?
Що таке комбінації? Поясніть формулу.
Поясніть схему «Вибір формули».
Поясніть схему «Вибір правила».
Як створити трикутник Паскаля?
Як розкласти біном Ньютона?
Задачі
Скоротіть дріб:
 ;
; ;
; ;
; .
.
Спростіть вираз:
 ;
;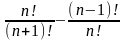 .
.
Обчисліть:
 ;
; ;
;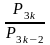 .
.
Знайдіть значення виразу:
 ;
;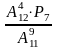 .
.
Доведіть, що
 .
.Розв’яжіть рівняння:
 ;
; .
.
У футбольній команді з 11 гравців треба обрати капітана та його заступника. Скількома способами це можна зробити?
У ліцеї в 9 класі вивчають 12 предметів. Денний розклад містить 6 уроків. Скількома способами можна скласти денний розклад?
Скільки існує трицифрових чисел, усі цифри яких непарні і різні?
Скільки існує звичайних дробів, чисельник і знаменник яких – різні прості числа, не більші за 20?
Обчисліть:
1)
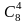 ;
2)
;
3)
;
2)
;
3)
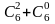 ;
4)
;
4)
 ;
5)
;
5)
 .
.
Доведіть, що:
 ;
; .
.
Розв’яжіть рівняння:
 ;
; ;
; ;
;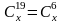 ;
; ;
; .
.
У класі 32 учня. Скількома способами можна сформувати команду з 4 чоловік для участі в математичній олімпіаді?
На площині розміщені 25 точок так, що ніякі три з них не лежать на одній прямій. Скільки існує трикутників з вершинами в цих точках?
Скількома способами можна групу з 17 учнів розділити на дві групи так, щоб в одній групі було 5 учнів, а в другій – 12 учнів?
Скільки можна скласти з простих дільників числа 2730 складених чисел, які мають тільки два простих дільника?
Даю вам також типовий варіант перевірочної роботи, щоб ви спробували.
Варіант 1
1 Знайдіть A U В і А В, якщо А = (- ; 5), В = [2; 6]. (2 бали)
2 Скількома способами можна скласти список з 9 чоловік? (2 бали)
3 Скільки різних прямих можна провести через 5 точок площини, з яких ніякі три не лежать на одній прямій? (2 бали)
4 Скількома способами можна з 20 чоловік призначити двох чергових, з яких один — старший? (2 бали)
5 Розкласти вираз (1 + )5 за формулою бінома Ньютона і спростити. (2 бали)
6 З 10 різних троянд і 5 різних гербер потрібно скласти букет, що містить 3 троянди і 2 гербери. Скільки різних букетів можна скласти? (2 бали)

