Закон инерции (I закон Ньютона)

Если на тело не действуют никакие силы или их равнодействующая равна нулю, то всегда можно найти такую систему отсчета, в которой данное тело движется равномерно и прямолинейно, либо покоится.

Этот закон выделяет из всех систем отсчета особый класс систем, которые принято называть инерциальными системами. Все законы классической механики установлены и выполняются только в инерциальных системах отсчета. Существует множество таких систем, поскольку любая система, движущаяся относительно инерциальной равномерно и прямолинейно, также является инерциальной.

Механический принцип относительности

Рассмотрим связь между характеристиками движения при переходе от одной инерциальной системы к другой.

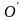Пусть некоторая система движется равномерно и прямолинейно со скоростью относительно неподвижной системы О. На рис. 1.13 для простоты принято, что координатные оси в этих системах ориентированы параллельно, и система движется вдоль оси х. В начальный момент ( ) начала отсчета обеих систем совпадают. Тогда очевидно, что координаты материальной точки m в этих системах отсчета в момент времени t связаны соотношениями, которые принято называть преобразования Галилея:

(1.34)

Из этих соотношений следует, что перемещения тел и их линейные размеры, определяемые как разность координат (например, 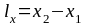), абсолютны (инвариантны), то есть одинаковы во всех инерциальных системах отсчета. Последнее равенство в системе (1.34) соответствует утверждению, что часы идут одинаково во всех инерциальных системах отсчета, следовательно: интервалы времени между двумя событиями ( ) так же абсолютны (инвариантны). Обобщая на случай произвольного направления движения системы , в векторной форме можно записать:

Дважды дифференцируя по времени это равенство, получим, во-первых, классический закон сложения скоростей:

(1.35)

скорость тела относительно неподвижной системы отсчета (абсолютная скорость) равна сумме скоростей движения этого тела относительно подвижной системы (относительной скорости) и движения подвижной системы относительно неподвижной (переносной скорости). Во-вторых, закон инвариантности ускорения: 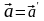ускорения тел одинаковы во всех инерциальных системах отсчета.

Итак, приходим к выводу, что хотя координаты и скорость тела могут иметь разные значения в разных системах отсчета, но оценка изменения состояния движения (то есть и 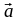) не зависят от выбора системы отсчета. Этот вывод и составляет содержание механического принципа относительности или принципа равноправия всех инерциальных систем отсчета. Обычно его формулируют следующим образом:

‒ все явления, связанные с изменением механического состояния тел, при одинаковых начальных условиях протекают одинаково во всех инерциальных системах отсчета;

‒ ни какими механическими опытами, произведенными внутри такой системы, невозможно установить движется система равномерно и прямолинейно или покоится;

‒ все законы механики имеют одинаковую форму во всех инерциальных системах отсчёта.