1.2.2. Кинематические законы

Кинематическими законами будем называть законы, выражающие изменение кинематических характеристик поступательного и вращательного движений с течением времени:

‒ закон пути и ;

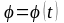‒ закон скорост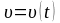и и ;

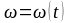‒ закон ускорения и .

Кинематические законы скорости и пути для поступательного и вращательного движений в общем виде

Если ускорение рассчитывается как производная от скорости по времени (см. определение), то скорость по отношению к ускорению является первообразной, а изменение скорости рассчитывается как интеграл. Аналогично далее: если модуль скорости рассчитывается как производная от пути по времени (см. определение), то путь по отношению к скорости является первообразной, а изменение длины пути рассчитывается как интеграл:

(1.13)

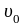Как видно, для решения задач на основе кинематических законов необходимо знать закон изменения ускорения с течением времени, а также начальные условия ‒ (или ), (или 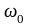), то есть положение и скорость тела в начальный момент .

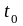Таблица 1.1

Кинематические законы для простейших видов движения

Движение	Закон ускорения	Закон скорости	Закон пути
Равномерное движение
Равнопеременное движение
Гармоническое колебательное движение

1.3. Динамика поступательного и вращательного движений

Основная задача динамики – установить причины, приводящие к изменению состояния движения тел, и факторы, определяющие ускорения, приобретаемые телами. В рамках классической механики рассматриваются только два фактора, влияющие на ускорение:

‒ внешние воздействия на тело;

‒ собственные инертные свойства тел.

1.3.1. Понятийный аппарат (динамические характеристики)

Величины, характеризующие интенсивность внешних воздействий при поступательном движении

1) Сила – векторная физическая величина, характеризующая интенсивность внешних воздействий (точнее взаимодействия тел) при поступательном движении. Ее численное значение измеряется либо на основании II закона Ньютона, либо (при статических проявлениях) путем сравнения с эталоном.

Направление вектора силы 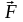определяется ее физической природой (например, сила трения всегда направлена по касательной к трущимся поверхностям в сторону противоположную относительной скорости движения тел). Результат действия силы не меняется, если точку ее приложения переносить вдоль линии действия силы.

2) Импульс силы – векторная физическая величина, характеризующая действие силы с учетом времени её действия. Направление импульса силы совпадает с направлением самой силы, а числовое значение определяется произведением силы на время её действия (если сила остается постоянной во время движения):

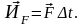(1.14)

Если сила изменяется с течением времени, то импульс силы вычисляется путем интегрирования:

(1.15)

3) Работа силы – скалярная физическая величина, характеризующая действие силы, с учетом расстояния, пройденного телом под действием этой силы, численно равная скалярному произведению векторов силы и перемещения.

При постоянной силе:

(1.16)

где – проекция силы на направление перемещения, – перемещение тела, α – угол между направлением силы и направлением перемещения.

При переменной силе работа вычисляется путем интегрирования, при этом можно учесть, что для бесконечно малых перемещений справедливо 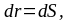поэтому:

(1.17)

Величины, характеризующие интенсивность внешних воздействий при вращательном движении

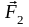П оскольку при поступательном движении тело рассматривается как материальная точка, все силы можно считать приложенными в одной точке – центре масс. Однако при рассмотрении вращательного движения этого делать нельзя, поскольку результат действия силы в этом случае существенно зависит от точки ее приложения. Если к телу, поочередно прилагать силы и , совпадающие по абсолютной величине и направлению, но приложенные на разных расстояниях от оси (рис. 1.10), то изменение состояния движения тела под действием силы , будет более значительным, чем под действием силы . Этот факт приводит к необходимости введения новой величины для характеристики воздействия тел друг на друга при вращательном движении.

П усть, на твердое тело, имеющее неподвижную ось вращения ОО, действует сила (рис. 1.11). Разложим эту силу на две составляющие: , действующую в плоскости, перпендикулярной оси вращения, и ‒ параллельную оси вращения. Составляющая не может вызвать вращательного движения вокруг оси ОО. Вращающее действие силы обусловлено ее составляющей .

1) Момент силы относительно оси – векторная физическая величина, характеризующая интенсивность внешних воздействий при вращательном движении, равная векторному произведению радиус-вектора , проведенного от оси вращения к точке приложения силы и лежащего в плоскости, перпендикулярной к оси вращения, на составляющую силы , действующую в этой же плоскости:

(1.18)

Вектор направлен вдоль оси вращения в ту сторону, откуда кратчайший переход от к происходит против часовой стрелки (то есть направление связано с направлением вращения тела под действием заданной силы правилом правого винта).

Модуль векторного произведения можно найти по следующей формуле:

. (1.19)

Как видно, из рис. 1.11, 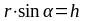, тогда

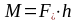, (1.20)

где 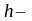плечо силы – кратчайшее расстояние от оси вращения до линии, вдоль которой действует сила ; – угол между положительными направлениями векторов и .

2) Импульс момента силы – векторная физическая величина, характеризующая действие момента силы с учетом времени его действия. Направление импульса момента силы совпадает с направлением момента силы, а числовое значение определяется произведением момента силы на время его действия (если момент силы остается постоянным во время движения):

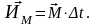(1.21)

Если момент силы изменяется с течением времени, то импульс момента силы вычисляется путем интегрирования:

(1.22)

3) Работа момента силы – скалярная физическая величина, характеризующая действие момента силы, с учетом углового перемещения, совершенного под действием этого момента силы, численно равная скалярному произведению векторов момента силы и углового перемещения.

При постоянном моменте силы:

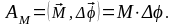(1.23)

При переменном моменте силы работа вычисляется путем интегрирования

(1.24)

Величины, характеризующие инертные свойства тел

Инертность – это способность тел в большей или меньшей степени изменять состояние движения под действием внешних сил. То тело, которое при заданном воздействии изменяет состояние своего движения в меньшей степени, считается более инертным.

1) Масса – скалярная физическая величина, характеризующая инертные свойства тел при поступательном движении (масса ‒ мера инертности). Относится к основным величинам системы СИ и определяется путем сравнения с эталоном.

Масса связана с объемом тела: , где ‒ плотность вещества, из которого состоит тело (табличная величина).

В ыясним, можно ли воспользоваться массой как характеристикой инертных свойств тел для вращательного движения тел. Пусть есть два колеса одинаковых внешних радиусов и одинаковые по массе, но у первого основная часть массы сосредоточена вблизи оси вращения, а обод колеса легкий, у второго, наоборот, основная часть массы сосредоточена по ободу (рис. 1.12). Будут ли эти колеса вести себя одинаково при одинаковых внешних воздействиях? Очевидно, нет. Второе колесо будет проявлять большую инертность: при одинаковых внешних воздействиях его угловая скорость будет меняться в меньшей степени, чем у первого колеса. Можно рассуждать и в обратном порядке: если мы захотели бы одинаково изменить угловую скорость вращения этих колес, то ко второму колесу пришлось бы приложить большие воздействия, чем к первому (второе колесо труднее разогнать и труднее остановить, следовательно, его инертность больше).

Таким образом, масса тела сама по себе не дает представления об инертных свойствах тел по отношению к вращательному движению. Инертность тел в этом случае зависит еще и от того, как распределена эта масса по отношению к оси вращения. В связи с этим вводится новая величина.

2) Момент инерции – скалярная физическая величина, характеризующая инертные свойства тел во вращательном движении. Для материальной точки момент инерции численно равен произведению массы точки на квадрат ее расстояния от оси вращения:

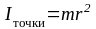, (1.25)

а для системы определяется суммой произведений масс отдельных точек на квадраты их расстояний от оси вращения:

(1.26)

Это вытекает из экспериментально установленного свойства аддитивности момента инерции, выражающегося в том, что момент инерции системы равен сумме моментов инерции отдельных частей этой системы (тело можно рассматривать как систему материальных точек).

Более строго, так как тело состоит из бесконечно большого числа материальных точек, а масса одной точки , момент инерции тела следует искать путем интегрирования:

, (1.27)

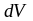где бесконечно малая часть массы тела, сосредоточенная в бесконечно малом объеме ; ‒ плотность вещества.

Результат интегрирования по формуле (1.27) зависит от распределения массы по отношению к оси вращения, то есть от формы тела и расположения оси вращения.

Таблица 1.2