3.7. Примеры решения задач по магнитному полю
Пример 1. Определить индукцию магнитного поля, создаваемого круговым витком, по которому течет ток, в центре витка. Радиус витка 5 см.
Решение.
В
данной задаче источником магнитного
поля является круговой виток, по которому
течет ток I.
Разобьем виток на маленькие элементы
длиной dl
и
найдем индукцию от одного такого элемента
по закону Био-Савара-Лапласа
.
Угол между элементом тока Idl
и
r
равен
,
следовательно
,
r
= R.
По принципу суперпозиции
(1)
Все векторы от разных элементов витка направлены по одной прямой в одну сторону «к нам», тогда на основании (1)
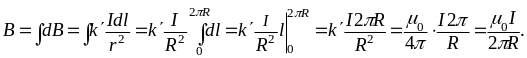(2)
Проверим выражение (2) по размерности:
Произведем вычисления:
Ответ:
Пример 2. Определить индукцию магнитного поля, создаваемого бесконечно длинным прямым проводником с током 5 А, в точке А, отстоящей от оси проводника на расстоянии 2,5 см.
Решение.
В
данной задаче источником магнитного
поля является б
есконечно
длинный прямой проводник, по которому
течет ток I.
На рис. 3.25
изображена
конфигурация силовых линий этого поля.
Для определения магнитной индукции в
точке А применим теорему о циркуляции
,
где
– циркуляция вектора В
по замкнутому контуру,
– сумма токов, охватываемых этим
контуром.
В
качестве замкнутого контура выберем
окружность, совпадающую с силовой
линией, проходящей через точку А.
Спроектируем
вектор
на касательную к контуру, в пределах
контура интегрирования
.
Циркуляция по выбранному контуру равна:
Внутри
выбранного контура находится только
ток I,
т.е.
Применим
теорему о циркуляции
,
следовательно
Проверим полученное выражение по размерности:
Произведем вычисления:
Ответ:
П
ример
3.
Два
параллельных бесконечно длинных провода
D
и
С,
по которым текут в одном направлении
электрические токи силой I
=
60 А, расположены на расстоянии d
=
10 см друг от друга перпендикулярно
плоскости чертежа. Определить магнитную
индукцию поля, создаваемого проводниками
с током в точке А
(рис.
3.26),
отстоящей
от оси одного проводника на расстоянии
= 5 см, от другого – на
= 12
см.
Решение.
В данной задаче источниками магнитного
поля а точке А
являются
два параллельных бесконечно длинных
провода D
и
С.
Для
нахождения магнитной индукции
в этой точке воспользуемся принципом
суперпозиции магнитных полей. Для этого
определим направления магнитных индукций
и
полей, создаваемых каждым проводником
с током в отдельности, и сложим их
геометрически:
Модуль
вектора
может
быть найден по теореме косинусов:
(1)
где
– угол между векторами
и
.
Магнитные
индукции
и
выражаются соответственно через силу
тока I
и расстояния
и
от проводов до точки А:
.
Подставляя
выражения
и
в формулу (1) и вынося
за знак корня, получаем
(2)
Вычислим
cos α.
Заметив, что α
=
DAC
(как углы с соответственно перпендикулярными
сторонами), по теореме косинусов запишем
,
где d – расстояние между проводами. Отсюда
;
.
Подставим в формулу (2) числовые значения физических величин и произведем вычисления:
Ответ: В=308 мкТл.
П
ример
4. Два
бесконечно длинных провода скрещены
под прямым углом (рис. 3.27). По проводам
текут токи I1
=
80 А и I2
=
60 А. Расстояние d
между проводами равно 10 см. Определить
магнитную индукцию В
в точке А, одинаково удаленной от обоих
проводов.
Р
ешение.
В
данной задаче магнитное поле создают
два бесконечно длинных провода, которые
скрещены под прямым углом. В соответствии
с принципом суперпозиции магнитных
полей магнитная индукция
поля, создаваемого токами
и
,
определяется выражением
,
где
– магнитная индукция поля, созданного
в точке А током
;
–
магнитная индукция поля, созданного в
точке А током
Заметим, что векторы
и
взаимно перпендикулярны (их направления
находятся по правилу буравчика и
изображены в двух проекциях на рис.
3.28). Тогда модуль вектора
можно определить по теореме Пифагора:
,
где
B1
и B2
определяются по формулам расчета
магнитной индукции для бесконечно
длинного прямолинейного провода с
током:
и
.
В нашем случае r0
=
d/2,
тогда
.
Произведем вычисления:
Ответ: В = 400 мкТл.
Пример
5.
Плоский квадратный контур со стороной
а
=
10 см, по которому течет ток I
=
100 А, свободно установился в однородном
магнитном поле (В
= 1
Тл). Определить работу А, совершаемую
внешними силами при повороте контура
относительно оси, проходящей через
середины его противоположных сторон,
на угол: 1)
;
2)
.
При повороте контура сила тока в нем поддерживается неизменной.
Р
ешение.
В
данной задаче внешние силы совершают
работу при повороте контура с током в
магнитном поле. На контур с током в
магнитном поле действует момент силы
(1)
где
–
магнитный момент контура; В
– магнитная индукция;
– угол между векторами
(направлен по нормали к контуру) и
,
рис. 3.29.
По условию задачи в начальном положении контур свободно установился в магнитном поле. При этом момент силы равен нулю (M = 0), а значит, , т.е. векторы и сонаправлены. Если внешние силы выведут контур из положения равновесия, то возникший момент сил будет стремиться возвратить контур в исходное положение. Против этого момента и будет совершаться работа внешними силами. Т.к. момент сил переменный и зависит от угла поворота , то для подсчета работы применим формулу работы в дифференциальной форме dА = Мdφ. Учитывая формулу (1), получаем
Взяв интеграл от этого выражения, найдем работу при повороте на конечный угол:
(2)
Работа при повороте на угол
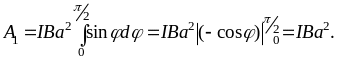(3)
Проверим данное выражение по размерности:
[A]=[I][B][S]=[А][Тл][м]2=[А][Вб]=Дж
Выразим числовые значения величин в единицах СИ (I = 100 А,
В = 1 Тл, а = 10 см = 0,1 м) и подставим в (3): A1 = 100·1·(0,1)2 = 1 Дж.
Работа при повороте на угол . В этом случае, учитывая, что угол φ2 мал, заменим в выражении (1) sinφ ≈ φ:
(4)
Выразим угол в радианах. После подстановки числовых значений величин в (4) найдем
А2 = 0,5·100·1·(0,1)2·(0,0523)2 = 1,37·10-3 Дж = 1,37 мДж.
Ответ: А1=1Дж; А2=1,37м Дж.
Пример 6. Протон, прошедший ускоряющую разность потенциалов U=600 В, влетел в однородное магнитное поле с индукцией В = 0,3 Тл и начал двигаться по окружности. Вычислить радиус R окружности.
Р
Рис.
3.30
удет
происходить по окружности только в том
случае, когда частица влетит в магнитное
поле перпендикулярно линиям магнитной
индукции, т.е.
,
рис. 3.30. На протон действует сила Лоренца,
которая перпендикулярна вектору
.
Она сообщает протону нормальное ускорение
.
Согласно второму закону Ньютона,
(1)
где m – масса протона.
На
рис. 3.30 совмещена траектория протона с
плоскостью чертежа и дано (произвольно)
направление вектора
.
Силу Лоренца направим перпендикулярно
вектору
к центру окружности (векторы
и
сонаправлены). Используя правило левой
руки, определим направление магнитных
силовых линий (направление вектора
).
Перепишем выражение (1) в скалярной форме (в проекции на ось, совпадающую с радиусом):
(2)
В
скалярной форме
В нашем случае
и sinα
=
l, тогда
.
Т.к. нормальное ускорение
,
то выражение (2) перепишем следующим
образом:
Отсюда находим радиус окружности:
Заметив, что mu есть импульс протона (р), это выражение можно записать в виде
(3)
Импульс протона найдем, воспользовавшись связью между работой сил электрического поля и изменением кинетической энергии протона, т.е. А = ΔТ, или
где
–
ускоряющая разность потенциалов (или
ускоряющее напряжение U);
и
– начальная и конечная кинетические
энергии протона.
Пренебрегая начальной кинетической энергией протона ( ≈ 0) и выразив кинетическую энергию через импульс р, получим
Найдем
из этого выражения импульс
и подставим его в формулу (3) (
):
или
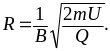(4)
Проверим
полученное выражение по размерности:
Подставим в формулу (4) числовые значения физических величин и произведем вычисления:
=
0,0118 м = 11,8 мм.
Ответ: R=11,8 мм.
Пример 7. Электрон движется в однородном магнитном поле (B = 10 мТл) по винтовой линии, радиус R которой равен 1 см и шаг h = 6 см. Определить период Т обращения электрона и его скорость u.
Р
ешение.
В данной задаче рассматривается движение
электрона в однородном магнитном поле.
Электрон будет двигаться по винтовой
линии, если он влетает в однородное
магнитное поле под некоторым углом (α
≠ π/2)
к линиям магнитной индукции. Разложим,
как это показано на рисунке 3.31, скорость
электрона на две составляющие: параллельную
вектору
(
)
и перпендикулярную ему (
).
Скорость
в магнитном поле не изменяется и
обеспечивает равнопеременное перемещение
электрона вдоль силовой линии. Скорость
в результате действия силы Лоренца
будет изменяться только по направлению
(
)
(в отсутствие параллельной составляющей
(
=
0) движение электрона происходило бы по
окружности в плоскости, перпендикулярной
магнитным силовым линиям). Таким образом,
электрон будет участвовать одновременно
в двух движениях: равномерном перемещении
со скоростью
и
равномерном движении по окружности со
скоростью
.
Период обращения электрона связан с перпендикулярной составляющей скорости соотношением
(1)
Найдем
отношение
Для этого воспользуемся тем, что сила
Лоренца сообщает электрону нормальное
ускорение
.
Согласно второму закону Ньютона можно
написать
или
(2)
Сократив
(2) на
,
выразим соотношение
(
)
и подставим его в формулу (1):
.
(3)
Модуль скорости u, как это видно из рис. 3.31, можно выразить через и :
Из формулы (2) выразим перпендикулярную составляющую скорости:
Параллельную
составляющую скорости
найдем из следующих соображений. За
время, равное периоду обращения Т,
электрон пройдет вдоль силовой линии
расстояние, равное шагу винтовой линии,
т.е.
h =
,
откуда
Подставив вместо Т правую часть выражения (1.12), получим
Таким образом, модуль скорости электрона
.
(4)
Проверим выражение (3) и (4) по размерности
Произведем
вычисления:
.
Ответ:
;
Пример 8. Альфа-частица прошла ускоряющую разность потенциалов U = 104 В и влетела в скрещенные под прямым углом электрическое (Е = 10 кВ/м) и магнитное (В = 0,1 Тл) поля со скоростью , перпендикулярной и . Найти отношение заряда альфа-частицы к ее массе, если, двигаясь перпендикулярно обоим полям, частица не испытывает отклонений от прямолинейной траектории.
Решение. В задаче рассматривается ситуация, когда альфа-частица движется сначала в электрическом поле, а затем влетает в скрещенные под прямым углом электрическое и магнитное поля. В электрическом поле альфа-частица движется вдоль силовых линий, проходит ускоряющую разность потенциалов и приобретает скорость , т.е. работа сил электрического поля и идет на изменение кинетической энергии частицы: QU = mu2/2, откуда
(1)
В скрещенных электрическом и магнитном полях на движущуюся заряженную частицу действуют две силы:
а)
сила Лоренца
,
направленная перпендикулярно скорости
и вектору магнитной индукции
;
б
)
кулоновская сила
,
сонаправленная с вектором напряженности
электростатического поля (Q
>
0). На рис. 3.32 направим вектор магнитной
индукции
вдоль оси OZ, скорость
– в положительном направлении оси
ОХ,
тогда
и
будут направлены так, как показано на
рисунке.
Альфа-частица
не будет испытывать отклонения, если
геометрическая сумма сил будет равна
нулю:
.
В проекции на ось ОY
получим следующее равенство (при этом
учтено, что
и
sinα
= 1):
QE - QuB = 0,
откуда
u = E/B.
Подставив это выражение скорости в формулу (1), получим
Проверим размерность:
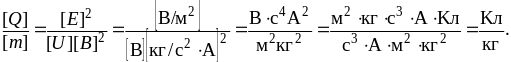
Произведем вычисления:
.
Ответ:
Пример
9.
Короткая
катушка, содержащая N
=
103
витков, равномерно вращается с частотой
n
=
10 с-1
относительно оси АС, лежащей в плоскости
катушки и перпендикулярной линиям
однородного магнитного поля (B
= 0,04
Тл).
Определить мгновенное значение ЭДС
индукции для тех моментов времени, когда
плоскость катушки составляет угол
=
60° с линиями поля. Площадь S
катушки равна 100 см2
(Рис. 3.33).
Р
ешение.
В данной задаче рассматривается катушка,
вращающееся в однородном магнитном
поле, в результате в ней возникает ЭДС
индукции, мгновенное значение
которой определяется основным уравнением
электромагнитной индукции Фарадея-Максвелла:
,
(1)
где N – число витков катушки, пронизываемых магнитным потоком Ф.
В
однородном магнитном поле по определению
Ф
= BScos
,
где В
– магнитная индукция; S
– площадь катушки;
− угол между вектором
и нормалью
.
При равномерном вращении катушки
,
где ω
− угловая скорость вращения катушки,
тогда магнитный поток Ф,
пронизывающий катушку в момент времени
t,
изменяется по закону Ф
= BScosωt.
Подставив в формулу (1) выражение
магнитного потока Ф
и продифференцировав по времени, найдем
мгновенное значение ЭДС индукции:
= NBSωsinωt.
Заметив, что угловая скорость ω связана с частотой вращения n катушки соотношением ω = 2πn и что угол ωt = π/2 - (рис. 3.33), получим (учтено, что sin(π/2 - ) = cos )
= 2πnNBScos .
Проверим выражение по размерности:
[ ]= [n][B][S]=[c-1][кг/А с2 м2]= кг м2/А с3=В.
Произведем вычисления:
= 2·3,14·10·103·0,04·10-2·0,5В = 25,1 В.
Ответ: = 25,1 В.
Пример 10. Квадратная проволочная рамка со стороной а = 5 см и сопротивлением R = 10 мОм находится в однородном магнитном поле (В = 40 мТл). Нормаль к плоскости рамки составляет угол α = 30° с линиями магнитной индукции. Определить заряд Q, который пройдет по рамке, если магнитное поле выключить.
Решение. В данной задаче рассматривается индукционный ток, который возникает в рамке, находящийся в изменяющимся во времени магнитном поле. При выключении магнитного поля произойдет изменение магнитного потока. Вследствие этого в рамке возникнет ЭДС индукции, определяемая основным законом электромагнитной индукции
Возникшая
ЭДС индукции вызовет в рамке индукционный
ток, мгновенное значение которого можно
определить воспользовавшись законом
Ома для полной цепи
,
где R
– сопротивление рамки. Тогда
Т.к.
мгновенное значение силы индукционного
тока
,
то это выражение можно переписать в
виде
,
откуда
.
(1)
Проинтегрировав выражение (1), найдем
,
или
.
Заметив, что при выключенном поле (конечное состояние) Ф2 = 0, последнее равенство перепишется в виде
(2)
Найдем магнитный поток Ф1. По определению магнитного потока для однородного поля имеем Ф1 = BScosα, где S – площадь рамки.
В нашем случае (рамка квадратная) S = а2. Тогда
(3)
Подставив
(3) в (2), получим
.
Проверим выражение по размерности:
Произведем вычисления:
.
Ответ:
