
- •Основы физики Механика. Электродинамика. Термодинамика
- •Оглавление
- •Глава 1. Основы классической механики 6
- •Глава 2. Основы релятивистской механики 68
- •Глава 3. Основы электродинамики 76
- •Глава 4. Основы молекулярной физики 163
- •4.1. Общие понятия 163
- •Предисловие
- •Введение
- •Глава 1. Основы классической механики
- •1.1. Общие понятия
- •1.2. Кинематика поступательного и вращательного движений
- •1.2.1. Понятийный аппарат (кинематические характеристики)
- •1.2.2. Кинематические законы
- •Кинематические законы скорости и пути для поступательного и вращательного движений в общем виде
- •Кинематические законы для простейших видов движения
- •1.3. Динамика поступательного и вращательного движений
- •1.3.1. Понятийный аппарат (динамические характеристики)
- •Формулы для вычисления моментов инерции некоторых тел
- •1.3.2. Динамические принципы и законы Принцип независимости действия сил
- •Закон инерции (I закон Ньютона)
- •Механический принцип относительности
- •Закон действия и противодействия (III закон Ньютона)
- •Основой закон динамики (II закон Ньютона)
- •Теоремы об изменении импульса и момента импульса тела
- •Теорема об изменении кинетической энергии
- •Разные формулировки основного закона динамики
- •1.3.3. Законы для разных видов сил. Потенциальная энергия взаимодействия
- •Особенности потенциальных сил. Потенциальная энергия взаимодействия тел.
- •1.4. Описание движения системы взаимодействующих тел
- •1.4.1. Понятийный аппарат
- •1.4.2. Основные законы для системы взаимодействующих тел Теорема о движении центра масс системы
- •Закон изменения импульса
- •Закон сохранения импульса
- •Закон изменения момента импульса
- •Закон сохранения момента импульса
- •Закон изменения полной механической энергии
- •Закон сохранения полной механической энергии
- •1.5. Примеры решения задач по механике
- •Контрольные вопросы
- •Список рекомендуемой литературы
- •Глава 2. Основы релятивистской механики
- •2.1. Общие понятия
- •2.2. Кинематические соотношения релятивистской механики
- •2.3. Динамические соотношения релятивистской механики
- •2.4. Примеры решения задач
- •Контрольные вопросы
- •Список рекомендуемой литературы
- •Глава 3. Основы электродинамики
- •3.1. Общие понятия
- •3.2. Электростатическое поле
- •3.2.1. Понятийный аппарат (характеристики электрического поля)
- •Графическое изображение электростатического поля
- •3.2.2. Основные законы и соотношения электростатики Закон сохранения электрического заряда
- •Теорема о циркуляции вектора е для электростатического поля
- •Теорема Остроградского – Гаусса (теорема о потоке вектора е) для электростатического поля
- •Расчет характеристик поля при известных зарядах, создающих поле
- •Принцип суперпозиции электрических полей
- •Действие электростатического поля на помещенные в него заряды
- •3.3. Магнитное поле
- •3.3.1. Понятийный аппарат (характеристики магнитного поля)
- •3.3.2. Основные законы и соотношения электромагнетизма Теорема о циркуляции вектора в для магнитного поля
- •Теорема Остроградского – Гаусса (теорема о потоке вектора в) для магнитного поля
- •Закон Био-Савара-Лапласа
- •Принцип суперпозиции магнитных полей
- •Расчет характеристик поля при известных токах, создающих поле
- •Действие магнитного поля на помещенные в него заряды и токи
- •3.3.3. Явление электромагнитной индукции
- •Закон Фарадея для явления электромагнитной индукции
- •3.4. Электрические и магнитные свойства вещества и тел
- •3.4.1. Электрические свойства вещества
- •Диэлектрики в электростатическом поле
- •Металлические проводники в электростатическом поле
- •Распределение статического избыточного заряда в металлических проводниках
- •Правила для последовательного и параллельного соединения конденсаторов
- •Металлические проводники в стационарном поле
- •Расчет цепей постоянного тока
- •Правила для последовательного и параллельного соединения проводников
- •3.4.2. Магнитные свойства вещества
- •Диамагнетики в магнитном поле
- •Парамагнетики в магнитном поле
- •3.5. Взаимосвязь электрического и магнитного полей. Полная система уравнений для электромагнитного поля
- •Система уравнений Максвелла для электромагнитного поля в вакууме
- •Уравнения, определяющие действие поля на находящиеся в нем заряды
- •Материальные уравнения
- •3 .6. Примеры решения задач по электрическому полю
- •3.7. Примеры решения задач по магнитному полю
- •Контрольные вопросы
- •Список рекомендуемой литературы
- •Глава 4. Основы молекулярной физики и термодинамики
- •4.1. Общие понятия
- •4.2. Статистический и термодинамический методы изучения термодинамических явлений
- •4.2.1. Понятийный аппарат (микропараметры молекул и их связь с макропараметрами термодинамического состояния вещества)
- •Связь давления газа с импульсами молекул, со средней кинетической энергией поступательного движения молекул, со скоростью и концентрацией молекул
- •4.2.2. Статистические законы
- •4.2.3. Термодинамические законы
- •Рассмотрим следствия из уравнения (4.17) в применении к простейшим термодинамическим процессам
- •Первое начало термодинамики
- •Расчет работы при изменении объёма газа
- •Расчет количества теплоты при изменении температуры газа
- •Применение первого начала термодинамики к простейшим термодинамическим процессам
- •4.3. Превращение внутренней энергии в механическую. Принцип действия тепловой машины
- •4.4. Примеры решения задач по термодинамике
- •Контрольные вопросы
- •Список рекомендуемой литературы
- •5. Задачи для самостоятельного решения Требования к оформлению контрольных работ
- •Механика
- •Электрическое поле
- •Магнитное поле
- •Термодинамика
- •Заключение
- •Библиографический список
- •Приложение
- •Физические постоянные
- •Астрономические величины
- •Плотность твердых тел
- •Удельное сопротивление металлов
- •Относительные атомные массы Ar и порядковые номера z некоторых элементов
- •Механические, термодинамические, электрические единицы си, имеющие специальные наименования
- •Множители и приставки для образования десятичных кратных и дольных единиц и их наименования
- •Греческий алфавит
- •Направления
- •Направления:
- •Специалитет:
- •Основы физики. Механика. Электродинамика. Термодинамика
- •672039, Г.Чита, ул. Александро-Заводская, 30
- •672039, Г. Чита, ул. Александро-Заводская, 30
Закон изменения импульса
Изменение суммарного импульса всех тел, образующих систему, равно сумме импульсов внешних сил, действующих на систему:
 (1.60)
(1.60)
Закон сохранения импульса
При любых взаимодействиях тел внутри замкнутой системы векторная сумма импульсов тел, образующих систему, остается постоянной.
При решении задач закон сохранения импульса предпочтительнее выражать следующим образом:
 (1.61)
(1.61)
‒ векторная сумма импульсов тел системы в первом состоянии (I) равна векторной сумме импульсов тел системы во втором состоянии (II), если при переходе системы из первого состояния во второе на систему не действовали внешние силы, или их векторная сумма оказалась равной нулю (то есть, если система оставалась замкнутой).
Закон изменения момента импульса
Изменение суммарного момента импульса всех тел, образующих систему, равно сумме импульсов моментов внешних сил, действующих на систему:
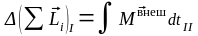 (1.62)
(1.62)
Закон сохранения момента импульса
При любых взаимодействиях тел внутри замкнутой системы векторная сумма моментов импульсов тел, образующих систему, остается постоянной.
При решении задач закон сохранения момента импульса предпочтительнее выражать следующим образом:
 (1.63)
(1.63)
‒ векторная сумма моментов импульсов тел системы в первом состоянии (I) равна векторной сумме моментов импульсов тел системы во втором состоянии (II), если при переходе системы из первого состояния во второе на систему не действовали внешние силы, или векторная сумма моментов этих сил оказалась равной нулю (то есть, если система оставалась замкнутой).
Закон изменения полной механической энергии
Изменение полной механической энергии системы определяется суммой работ внешних и внутренних непотенциальных сил.
 (1.64)
(1.64)
Отсюда следует, что действие потенциальных сил не приводит к изменению полной механической энергии системы. Если на тела системы действуют только потенциальные силы, то может происходить переход кинетической энергии в потенциальную и обратно, но механическая энергия при этом не переходит в другие виды (например, в тепловую).
Закон сохранения полной механической энергии
Полная механическая энергия системы остается постоянной, если работа внешних сил равна нулю (то есть, система замкнутая) и внутри системы действуют только потенциальные силы или работа непотенциальных сил равна нулю (то есть система консервативная):
 (1.65)
(1.65)
1.5. Примеры решения задач по механике
Пример
1.
Тело вращается вокруг неподвижной оси
по закону
 где
А
= 10
рад,
В = 20
рад/с,
С = -2
рад/с2.
Найти скорость и ускорение точки,
находящейся на расстоянии r
=
0,1
м
от оси вращения, для момента времени t
=
4
с.
Показать векторы скорости и ускорения
на рисунке.
где
А
= 10
рад,
В = 20
рад/с,
С = -2
рад/с2.
Найти скорость и ускорение точки,
находящейся на расстоянии r
=
0,1
м
от оси вращения, для момента времени t
=
4
с.
Показать векторы скорости и ускорения
на рисунке.
Решение.
В
данной задаче рассматривается вращательное
движение вокруг неподвижной оси, где
по известному закону изменения угла
поворота необходимо найти изменения с
течением времени других кинематических
характеристик и их значение в заданный
момент времени. Скорость точки тела,
вращающегося вокруг неподвижной оси,
определяется по формуле
 ,
где w
– модуль
угловой скорости тела. Угловую скорость
w
найдем, взяв первую производную от угла
поворота по времени:
,
где w
– модуль
угловой скорости тела. Угловую скорость
w
найдем, взяв первую производную от угла
поворота по времени:
 (1)
(1)
П олное
ускорение точки, движущейся по кривой
линии, может быть найдено как геометрическая
сумма тангенциального ускорения
,
направленного по касательной к траектории,
и нормального ускорения
,
направленного к центру кривизны
траектории (рис.
1.22):
олное
ускорение точки, движущейся по кривой
линии, может быть найдено как геометрическая
сумма тангенциального ускорения
,
направленного по касательной к траектории,
и нормального ускорения
,
направленного к центру кривизны
траектории (рис.
1.22):

Так как векторы взаимно перпендикулярны, то модуль ускорения:
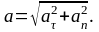 (2)
(2)
Модули тангенциального и нормального ускорения точки вращающегося тела выражаются формулами:
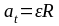 ,
,
 ,
(3)
,
(3)
где e – модуль его углового ускорения.
Подставляя выражения аt и аn в формулу (2), находим
 .
(4)
.
(4)
Проверим, дает ли полученная формула единицу а. Для этого в правую часть формулы (4) вместо величин подставим их единицы измерения:

Угловое ускорение найдем, взяв первую производную от угловой скорости (1) по времени:
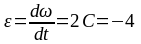 рад/с2.
рад/с2.
Вектор
касательного ускорения направлен против
скорости, т.к. угловое ускорение

Найдем значение скорости и ускорения точки, находящейся на расстоянии r = 0,1 м от оси вращения, для момента времени t = 4 с. В момент времени t = 4 c модуль угловой скорости

Скорость
точки
 м/с.
м/с.
Подставляя значения w, e и r в формулу (4), получаем
 м/с2.
м/с2.
Ответ:
 м/с,
м/с,
 м/с2.
м/с2.
Пример 2. Материальная точка движется в соответствии с уравнениями:
x=A+Bt+Ct3, y=Kt+Lt2, (1)
где А = 3 м, В = 1 м/с, С = -1 м/с3, K = 1,5 м/с, L = 2 м/с2.
Найти координаты, скорость и ускорение точки в момент времени t=1 c.
Решение. В задаче рассматривается поступательное движение, где по известному закону изменения движения необходимо найти изменения с течением времени других кинематических характеристик и их значение в заданный момент времени. В данной задаче закон движения задан не вдоль траектории, а в проекциях на координатные оси.
Проекции мгновенной скорости точки на оси х, y есть первые производные от координат (1) по времени:
 ,
,
 .
(2)
.
(2)
Полная
скорость находится выражением:
 .
.
Проекции ускорения точки найдем, взяв первые производные от проекций скорости (2) по времени:
 ,
,
 .
(3)
.
(3)
Модуль
ускорения точки
 .
.
Найдем координаты, скорость и ускорение точки в момент времени t=1 c. Координаты точки найдем, подставив в уравнения движения (1) числовые значения коэффициентов А, В, С, K, L и времени t:
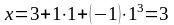 ,
,
 .
.
При
t
=
1 c,
 ;
;
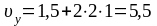 .
Модуль скорости
.
Модуль скорости м/с.
м/с.
При
t
=
1 c
 м/с2,
м/с2,
 м/с2,
м/с2,
 м/с2.
м/с2.
Ответ:
х=3
м, y=3,5
м,
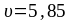 м/с,
м/с,
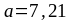 м/с2.
м/с2.
Пример
3.
Материальная точка брошена с начальной
скоростью
 м/с
под углом α
= 60 ° к
горизонту. Найти скорость точки и радиус
кривизны траектории в момент времени
t1
=
2 c.
м/с
под углом α
= 60 ° к
горизонту. Найти скорость точки и радиус
кривизны траектории в момент времени
t1
=
2 c.
Р
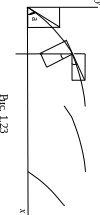 ешение.
В
задаче рассматривается сложное
криволинейное движение тела в поле силы
тяжести Земли. На основании принципа
независимости движений его можно
представить состоящим из двух движений
– по горизонтали (по оси х)
и по вертикали (по оси у).
Характер поступательного движения
определяется на основе II
закона Ньютона, а конкретные параметры
движения на основе кинематических
законов.
ешение.
В
задаче рассматривается сложное
криволинейное движение тела в поле силы
тяжести Земли. На основании принципа
независимости движений его можно
представить состоящим из двух движений
– по горизонтали (по оси х)
и по вертикали (по оси у).
Характер поступательного движения
определяется на основе II
закона Ньютона, а конкретные параметры
движения на основе кинематических
законов.
Второй
закон Ньютона:
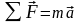 .
На материальную точку действует
единственная сила – сила тяжести
.
На материальную точку действует
единственная сила – сила тяжести
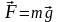 .
В проекциях на координатные оси:
.
В проекциях на координатные оси:
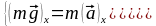 По рисунку 1.23 видно, что
По рисунку 1.23 видно, что
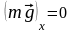 ,
,
 ,
тогда
,
тогда
 ‒ движение по оси х
равномерное,
‒ движение по оси х
равномерное,
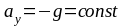 ‒ движение по оси у
равнопеременное.
‒ движение по оси у
равнопеременное.
Запишем кинематические законы для этих видов движения:

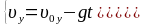 (1)
(1)
Модуль скорости определяется выражением:
 (2)
(2)
Модуль полного ускорения равен
 (3)
(3)
Из
рис. 1.23 определим
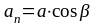 ,
где β
– угол между полным ускорением и
нормальным ускорением в момент времени
,
где β
– угол между полным ускорением и
нормальным ускорением в момент времени
 .
Также из рисунка получаем, что
.
Также из рисунка получаем, что

По
определению нормальное ускорение точки
равно
 .
Тогда радиус кривизны траектории
.
Тогда радиус кривизны траектории

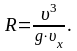 (4)
(4)
Проверим, дает ли полученная формула единицу R. Для этого в правую часть формулы (4) вместо величин подставим их единицы измерения:

Определим скорость точки, и радиус кривизны траектории в момент времени = 2 c.


Ответ: = 16,3 м/с, R = 29,46 м.
Пример
4. Через
блок в виде сплошного диска, имеющего
массу
 (рис.
1.24),
перекинута невесомая нерастяжимая
нить, к концам которой подвешены грузы
с массами m1
=
100
г
и m2
=
200
г.
Определить ускорение, с которым будут
двигаться грузы, если их предоставить
самим себе. Трением и массой нити
пренебречь.
(рис.
1.24),
перекинута невесомая нерастяжимая
нить, к концам которой подвешены грузы
с массами m1
=
100
г
и m2
=
200
г.
Определить ускорение, с которым будут
двигаться грузы, если их предоставить
самим себе. Трением и массой нити
пренебречь.
Р ешение.
В данной задаче рассматривается движение
тел относительно поверхности Земли.
Систему отсчета связанную с Землей
можно считать инерциальной, и в ней
применимы законы Ньютона. В
движении участвуют три тела. Грузы
массами
и
движутся поступательно, а блок вращается.
ешение.
В данной задаче рассматривается движение
тел относительно поверхности Земли.
Систему отсчета связанную с Землей
можно считать инерциальной, и в ней
применимы законы Ньютона. В
движении участвуют три тела. Грузы
массами
и
движутся поступательно, а блок вращается.
Рассмотрим
силы, действующие на каждое из тел. На
грузы действуют силы со стороны Земли
 и
и
 ,
и со стороны нити
,
и со стороны нити
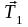 и
и
 .
Если нить не проскальзывает по блоку,
то можно считать, что вращение блока
вызывается действием сил натяжения
нити
.
Если нить не проскальзывает по блоку,
то можно считать, что вращение блока
вызывается действием сил натяжения
нити
 и
и
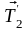 ,
причем во всех точках слева от блока
натяжение нити можно считать одинаковым
(так как нить по условию невесомая),
поэтому по численному значению
,
причем во всех точках слева от блока
натяжение нити можно считать одинаковым
(так как нить по условию невесомая),
поэтому по численному значению
 и аналогично справа от блока
и аналогично справа от блока
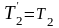 .
Кроме того на блок действует сила тяжести
.
Кроме того на блок действует сила тяжести
 и сила реакции опоры (сила упругости со
стороны оси)
и сила реакции опоры (сила упругости со
стороны оси)
 .
.
Когда система состоит из нескольких тел, уравнение II закона Ньютона записывается для каждого тела в отдельности.
Для тела в проекции на ось x:
 (1)
(1)
Для тела в проекции на ось x:
 (2)
(2)
Для блока:
 (блок
поступательно не движется). (3)
(блок
поступательно не движется). (3)
Чтобы записать II закон Ньютона для вращательного движения блока, рассмотрим моменты сил, действующих на блок, приняв направление вдоль оси вращения "от нас" за положительное направление оси z.
Линии
действия сил
и
проходят через ось вращения, следовательно,
их моменты равны нулю. Момент силы
 в проекции на ось z:
в проекции на ось z:
 .
Момент силы
.
Момент силы
 в проекции на ось z:
в проекции на ось z:
 ,
где R
‒ радиус блока.
,
где R
‒ радиус блока.
Таким образом, II закон Ньютона для вращательного движения блока:
 (4)
(4)
где
 ‒ момент инерции блока как сплошного
диска равен
‒ момент инерции блока как сплошного
диска равен

Движения
тел не являются независимыми. Так, из
условия нерастяжимости нити следует,
что
 ,
из условия отсутствия проскальзывания
нити по блоку тангенциальное ускорение
точек блока в месте соприкосновения с
нитью равно ускорению нити и груза,
тогда
,
из условия отсутствия проскальзывания
нити по блоку тангенциальное ускорение
точек блока в месте соприкосновения с
нитью равно ускорению нити и груза,
тогда
 .
.
Уравнение
(4) с учетом выражений для
и
 :
:
 (5)
(5)
вычитая из (2) (1) с учетом (5) получим:

отсюда
 (6)
(6)
Проверим полученную формулу по размерности:
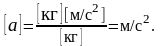
После подстановки числовых значений в формулу (6) получим

Ответ: а = 2,88 м/с2.
П ример
5.
Автомобиль массой
ример
5.
Автомобиль массой
 кг движется с постоянной скоростью
кг движется с постоянной скоростью
 по выпуклому мосту, радиус кривизны
которого 90 м. Найти силу давления
автомобиля на мост в точке, положение
которой задается углом
по выпуклому мосту, радиус кривизны
которого 90 м. Найти силу давления
автомобиля на мост в точке, положение
которой задается углом
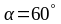 (см. рис. 1.25)
(см. рис. 1.25)
Решение.
В
задаче рассматривается криволинейное
поступательное движение. Выберем
координатные оси так, чтобы они в любой
момент времени совпадали с касательной
и нормалью к траектории. Так как автомобиль
движется с постоянной скоростью,
и сумма проекций сил тяжести, тяги и
трения на касательную к траектории тоже
равна нулю. Полное ускорение, таким
образом, сводится к нормальной
составляющей, которая направлена вдоль
радиуса к центру кривизны и определяется
суммой проекций силы
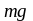 и силы реакции опоры на ось y.
(Силы тяги и трения не имеют проекций
на эту ось). Запишем II
закон Ньютона в виде
и силы реакции опоры на ось y.
(Силы тяги и трения не имеют проекций
на эту ось). Запишем II
закон Ньютона в виде
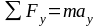 .
.
 (1)
(1)
откуда

Искомая
сила давления автомобиля на мост связана
с силой реакции
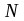 третьим законом Ньютона и по численному
значению равна
третьим законом Ньютона и по численному
значению равна
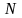 :
:
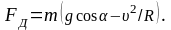 (2)
(2)
Проверим исходную формулу по размерности:

Вычислим силу давления автомобиля:

Ответ:

Пример
6.
Маховик в виде сплошного диска радиусом
R
=
0,2
м
и массой m
=
50
кг
раскручен до частоты вращения
 =
480
мин-1
и предоставлен сам себе. Под действием
сил трения маховик остановился через
t
=
50
с.
Найти момент М
сил
трения.
=
480
мин-1
и предоставлен сам себе. Под действием
сил трения маховик остановился через
t
=
50
с.
Найти момент М
сил
трения.
Решение. В задаче рассматривается вращательное движение маховика под действием силы трения. Для решения воспользуемся основным уравнением динамики вращательного движения в виде
 (1)
(1)
где
 – изменение проекции на ось z
момента
импульса маховика, вращающегося
относительно оси z,
совпадающей
с геометрической осью маховика, за
интервал времени
;
– изменение проекции на ось z
момента
импульса маховика, вращающегося
относительно оси z,
совпадающей
с геометрической осью маховика, за
интервал времени
;
 –
момент внешних сил (в данном случае
момент сил трения), действующих на
маховик относительно оси z.
–
момент внешних сил (в данном случае
момент сил трения), действующих на
маховик относительно оси z.
Момент
сил трения можно считать не изменяющимся
с течением времени ( ),
поэтому интегрирование уравнения (1)
приводит к выражению
),
поэтому интегрирование уравнения (1)
приводит к выражению
 .
(2)
.
(2)
При вращении твердого тела относительно неподвижной оси изменение проекции момента импульса
 (3)
(3)
где
 – момент инерции маховика относительно
оси z;
Dw
–
изменение угловой скорости маховика.
– момент инерции маховика относительно
оси z;
Dw
–
изменение угловой скорости маховика.
Приравняв
правые части равенств (2) и (3), получим
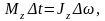 откуда
откуда
 (4)
(4)
Момент инерции маховика в виде сплошного диска определяется по формуле
 (5)
(5)
Изменение
угловой скорости
 выразим через конечную
выразим через конечную
 и начальную
частоты
вращения, пользуясь соотношением
и начальную
частоты
вращения, пользуясь соотношением
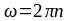 :
:
 .
(6)
.
(6)
Подставив
в формулу (4) выражения
(5) и
 (6)
,
получим
(6)
,
получим
 (7)
(7)
Проверим, дает ли расчетная формула единицу момента силы (Нм). Для этого в правую часть формулы вместо символов величин подставим их единицы:
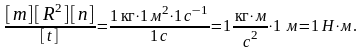
Подставим
в (7) числовые значения величин и произведем
вычисления, учитывая, что
=480
мин -1 с-1=8
с-1:
с-1=8
с-1:
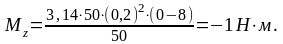
Знак минус показывает, что момент сил трения оказывает на маховик тормозящее действие.
Ответ:
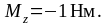
Пример
7.
Снаряд, летевший горизонтально со
скоростью
 ,
разрывается на две равные части на
высоте
,
разрывается на две равные части на
высоте
 .
Одна часть падает через время
.
Одна часть падает через время
 с на землю точно под местом взрыва.
Определить величину и направление
скорости второй части снаряда сразу
после взрыва.
с на землю точно под местом взрыва.
Определить величину и направление
скорости второй части снаряда сразу
после взрыва.
Решение.
В данной задаче рассматривается
поступательное движение, и взаимодействие
тел образующих систему снаряд - две его
части. Обозначим массу одной части ‒
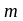 ,
тогда масса снаряда ‒
,
тогда масса снаряда ‒
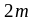 .
Внешние силы по отношению к этой системе
‒ это сила тяжести и сила сопротивления
воздуха. Внутренние силы, возникающие
при взрыве, не являются потенциальными,
а по величине много больше, чем внешние,
поэтому в интервале времени действия
внутренних сил систему можно считать
замкнутой, но не консервативной. Тела,
образующие систему, движутся поступательно,
поэтому применим закон сохранения
импульса.
.
Внешние силы по отношению к этой системе
‒ это сила тяжести и сила сопротивления
воздуха. Внутренние силы, возникающие
при взрыве, не являются потенциальными,
а по величине много больше, чем внешние,
поэтому в интервале времени действия
внутренних сил систему можно считать
замкнутой, но не консервативной. Тела,
образующие систему, движутся поступательно,
поэтому применим закон сохранения
импульса.
I
состояние ‒ две части снаряда движутся
как одно целое со скоростью
.
 ‒ вектор
‒ вектор
 направлен горизонтально.
направлен горизонтально.
II
состояние ‒ сразу после взрыва I-я часть
снаряда получает скорость
 ,
направленную вертикально вниз, а вторая
часть скорость
,
направленную вертикально вниз, а вторая
часть скорость
 ,
направление которой нужно определить
,
направление которой нужно определить

На
основании закона сохранения импульса

 .
(1)
.
(1)
Н аправление
векторов
аправление
векторов
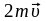 и
и
 известно по условию, на основании (1)
вектор
известно по условию, на основании (1)
вектор
 следует построить таким образом, чтобы
в сумме с
он дал вектор
.
следует построить таким образом, чтобы
в сумме с
он дал вектор
.
Дальнейшее решение можно вести в проекциях на координатные оси или воспользоваться соотношением между модулями векторов на основании рисунка 1.26 (векторы образуют прямоугольный треугольник)
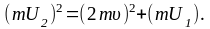 (2)
(2)
Из (2) следует
 (3)
(3)
Из
рисунка
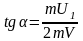

После
прекращения действия взрывных сил части
снаряда движутся под действием силы
тяжести (без учета сопротивления
воздуха). Первая часть снаряда движется
вертикально вниз с постоянным ускорением
g,
поэтому
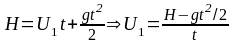 ,
с учетом числовых данных
,
с учетом числовых данных
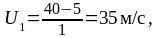


Ответ:
 ;
;

Пример 8. Платформа в виде сплошного диска радиусом R = 1,5 м и массой m1 = 180 кг вращается около вертикальной оси с частотой n = 10 мин-1. В центре платформы стоит человек массой m2 = 60 кг. Какую линейную скорость относительно пола помещения будет иметь человек, если он перейдет на край платформы?
Решение.
В данной задаче рассматривается
вращательное движение, и взаимодействие
тел образующих систему платформа ‒
человек. Внешними по отношению к этой
системе являются силы тяжести и реакции
оси, но линия их действия проходит через
ось вращения, момент этих сил равен
нулю, следовательно, систему можно
считать замкнутой по отношению к закону
сохранения момента импульса. Выделим
два состояние: I
состояние ‒ человек находится в центре
платформы и вся система вращается с
угловой скоростью
.
II
состояние – человек находится на краю
платформы и вся система вращается с
угловой скоростью
 ,
где
– скорость человека относительно пола.
Так как ось вращения неподвижна, то
векторы момента импульса тел в I
и во II
состоянии направлены по одной прямой
(вдоль оси) и закон сохранения момента
импульса можно сразу писать в проекции
на эту ось (z)
,
где
– скорость человека относительно пола.
Так как ось вращения неподвижна, то
векторы момента импульса тел в I
и во II
состоянии направлены по одной прямой
(вдоль оси) и закон сохранения момента
импульса можно сразу писать в проекции
на эту ось (z)
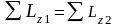 ,
(1)
,
(1)
По
определению
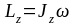 ,
где
– момент инерции платформы с человеком
относительно оси z;
w
– угловая скорость платформы.
,
где
– момент инерции платформы с человеком
относительно оси z;
w
– угловая скорость платформы.
Момент
инерции системы равен сумме моментов
инерции тел, входящих в состав системы,
поэтому в
I
состоянии
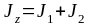 ,
а во II
состоянии
,
а во II
состоянии
 .
.
С учетом этого равенство (1) примет вид
![]() (2)
(2)
где
значения моментов инерции
![]() и
и
![]() платформы
и человека соответственно относятся к
I
состоянию
системы;
платформы
и человека соответственно относятся к
I
состоянию
системы;
![]() и
и
![]() – ко
II
состоянию
системы.
– ко
II
состоянию
системы.
Момент инерции платформы относительно оси z при переходе человека не изменяется:
![]()
Момент
инерции человека относительно той же
оси будет изменяться. Если рассматривать
человека как материальную точку, то его
момент инерции
в
I
состоянии (в центре платформы) можно
считать равным нулю. Во
II
состоянии
(на краю платформы) момент инерции
человека
![]() .
.
Подставим в формулу (2) выражения моментов инерции и угловой скорости вращения платформы с человеком в I и во II состоянии:
![]() (3)
(3)
После
сокращения на
![]() и простых преобразований находим
скорость:
и простых преобразований находим
скорость:
![]() (4)
(4)
Проверим, дает ли расчетная формула (4) единицу скорости (м/с). Для этого в правую часть формул вместо символов величин подставим их единицы:
![]()
Произведем
вычисления:
![]() .
.
Ответ:
![]()
Пример 9. Ящик массой m1 = 20 кг соскальзывает по лотку длиной l = 2 м с коэффициентом трения µ=0,1 на неподвижную тележку с песком и застревает в нем. Тележка с песком массой m2 = 80 кг может свободно (без трения) перемещаться по рельсам в горизонтальном направлении. Определить скорость и тележки с ящиком, если лоток наклонен под углом a = 30° к рельсам.
Решение.
В данной задаче рассматривается
поступательное движение двух систем
взаимодействующих тел «ящик-лоток-Земля»
и «ящик-тележка». Рассмотрим систему
«ящик-лоток-Земля». Внешних по отношению
к этим системам сил нет. Внутренними
являются сила тяжести G1
= m1g,
сила реакции опоры
![]() и
сила трения
и
сила трения
![]() .
Силы тяжести и реакции опоры (упругости)
являются потенциальными силами, а
действие непотенциальных сил трения
приводит к превращению механической
энергии в другие виды. Следовательно,
систему можно считать замкнутой, но не
консервативной, а изменение механической
энергии системы будет равно работе силы
трения
.
Силы тяжести и реакции опоры (упругости)
являются потенциальными силами, а
действие непотенциальных сил трения
приводит к превращению механической
энергии в другие виды. Следовательно,
систему можно считать замкнутой, но не
консервативной, а изменение механической
энергии системы будет равно работе силы
трения
![]() ,
где
,
где
![]() а
β
– угол между направлением силы трения
и направлением перемещения ящика. В
данной задаче β=1800,
а
β
– угол между направлением силы трения
и направлением перемещения ящика. В
данной задаче β=1800,
![]() ,
следовательно, работа силы трения равна
,
следовательно, работа силы трения равна
![]() .
.
Сила
реакции опоры
,
находится из второго закона Ньютона
![]() в проекциях на ось перпендикулярную
лотку (см.
рис.1.27).
Движения вдоль этой оси нет, поэтому
в проекциях на ось перпендикулярную
лотку (см.
рис.1.27).
Движения вдоль этой оси нет, поэтому
![]() .
Следовательно, сила трения определяется
выражением:
.
Следовательно, сила трения определяется
выражением:
![]() .
(1)
.
(1)
Рассмотрим
два состояния. I
состояние ‒ ящик находится в верхней
точке лотка в состоянии покоя
![]() .
Примем за нулевой уровень потенциальной
энергии положение ящика в конце лотка,
тогда
.
Примем за нулевой уровень потенциальной
энергии положение ящика в конце лотка,
тогда
![]() ,
где
,
где
![]() (из
рис.1.27).
II
состояние ящик находится в нижней точке
лотка
(из
рис.1.27).
II
состояние ящик находится в нижней точке
лотка
![]() ,
но при этом он движется. Кинетическая
энергия ящика перед падением на тележку
равна
,
но при этом он движется. Кинетическая
энергия ящика перед падением на тележку
равна
![]() .
Лоток и Земля не меняют своего состояния
движения. На основании закона изменения
энергии:
.
Лоток и Земля не меняют своего состояния
движения. На основании закона изменения
энергии:
![]() .
.
![]() (2)
(2)
Т ележку
и ящик можно рассматривать как систему
двух неупруго взаимодействующих тел.
Но эта система не замкнута, так как на
нее действуют внешние силы: силы тяжести
G1
= m1g
и
G2
=
m2g
и
сила реакции
N
(рис. 1.27). Поэтому применить закон
сохранения импульса в общем к системе
«ящик – тележка» нельзя. Однако, так
как проекции указанных сил на направление
оси х,
совпадающей
с направлением рельсов, равны нулю, то
проекцию импульса системы на это
направление можно считать постоянной,
т.е.
ележку
и ящик можно рассматривать как систему
двух неупруго взаимодействующих тел.
Но эта система не замкнута, так как на
нее действуют внешние силы: силы тяжести
G1
= m1g
и
G2
=
m2g
и
сила реакции
N
(рис. 1.27). Поэтому применить закон
сохранения импульса в общем к системе
«ящик – тележка» нельзя. Однако, так
как проекции указанных сил на направление
оси х,
совпадающей
с направлением рельсов, равны нулю, то
проекцию импульса системы на это
направление можно считать постоянной,
т.е.
![]() (3)
(3)
где
![]() и
и
![]() – проекции импульса ящика и тележки с
песком в момент падения ящика на тележку;
– проекции импульса ящика и тележки с
песком в момент падения ящика на тележку;
![]() и
и
![]() –
те же величины после падения ящика.
–
те же величины после падения ящика.
Р
![]() ,
или
,
или
![]() (4)
(4)
где
![]() –
модуль скорости ящика перед падением
на тележку;
–
модуль скорости ящика перед падением
на тележку;
![]() – проекция этой скорости на ось х.
– проекция этой скорости на ось х.
Из (4) следует
![]() (5)
(5)
Модуль скорости определим из выражения (2) с учетом (1)
![]() (7)
(7)
Подставив выражение в формулу (5), получим
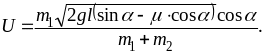 (8)
(8)
Проверим, дает ли полученная формула единицу скорости. Для этого в правую часть формулы (8) вместо величин подставим их единицы измерения:
![]()

Вычисляем скорость тележки:
![]()
Ответ:
U![]() м/с2.
м/с2.
