7

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Филиал государственного образовательного учреждения

высшего профессионального образования

“Уфимский государственный нефтяной технический университет” в г. Салавате

(Филиал ГОУ ВПО УГНТУ в г. Салавате)

Кафедра “Оборудование предприятий нефтехимии и нефтепереработки”

Согласовано утверждаю Зав. Кафедрой опнн, доцент Зам. Директора по учебной работе ______________н.М. Захаров _______________г.И. Евдакимов

______________ _______________

Методические указания к лабораторной работе № 7 определение напряжений при внецентренном растяжении - сжатии

Дисциплина "Сопротивление материалов"

СОГЛАСОВАНО РАЗРАБОТАЛ

Инженер по охране труда Доцент кафедры ОПНН

____________ Г.В. Мангуткина ___________ Р.Р. Газиев

____________ ___________

Салават 2008

Методические указания предназначены для студентов очной, очно-заочной и заочной форм обучения специальности 240801 “Машины и аппараты химических производств” и рекомендуются к применению при выполнении лабораторных работ по дисциплинам “Сопротивление материалов”.

© Филиал ГОУ ВПО “Уфимский государственный нефтяной технический университет” в г. Салавате , 2008

Лабораторная работа № 7

Определение напряжений при внецентренном растяжении-сжатии

Цель работы - определить опытным путем величины нормальных напряжений в различных точках поперечного сечения бруса при его внецентренном нагружении и сравнить полученные значения с результатами, рассчитанными теоретически.

1 Теоретическая часть

Внецентренным растяжением или сжатием называется такой вид деформации, при котором внешняя продольная сила, приложенная с некоторым смещением от центральной оси бруса, вызывает в его сечениях одновременно два внутренних силовых фактора - продольную силу и изгибающий момент. Подобный вид деформации также возникает при одновременном нагружении бруса продольной силой и внешним изгибающим моментом, поэтому иногда называют изгибом с растяжением или сжатием.

Расстояние, на которое смещена внешняя продольная сила, носит название эксцентриситета (е). Точка приложения внешней силы называется полюсом силы (р) или центром давления. Величина изгибающего момента, возникающего в сечениях бруса, зависит от величины этого эксцентриситета и силы F. В результате одновременного действия продольной силы и изгибающего момента в поперечном сечении бруса нормальные напряжения распределяются неравномерно по треугольному закону (рисунок 1). В общем случае эти напряжения определяются по следующей зависимости

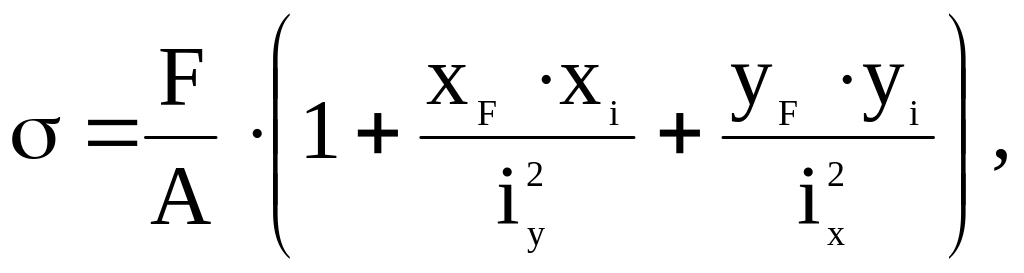(1)

где F - продольная сила, Н (растягивающая берется со знаком “+”, сжимающая со знаком “-”);

A - площадь поперечного сечения бруса, мм²;

х_F,y_F - координаты точки приложения нагрузки (центра давления), мм;

характеризуют величину эксцентриситета;

х_i ,у_i - координаты точки, в которой определяется напряжение, мм;

i _x , i _y - радиусы инерции поперечного сечения бруса, мм.

При внецентренном нагружении бруса нейтральная линия (линия нулевых напряжений) смещается от положения центра тяжести сечения, отсекая на осях “x” и “y” отрезки равные

Анализируя зависимости (2) можно сделать заключение о следующих свойствах нейтральной линии и центра давления:

- положение нейтральной линии не зависит от величины и направления приложенной нагрузки.

- нейтральная линия и центр давления всегда располагаются по разные стороны от центра тяжести сечения (на это указывает знак минус).

- чем ближе центр давления к центру тяжести, тем дальше от последнего располагается нейтральная линия и наоборот.

- координаты центра давления х_F и н_F взаимообратимы с отрезками, характеризующими положение нейтральной линии х_н.л. и у_н.л..

- если центр давления расположен на одной из главной, центральной оси сечения, то нейтральная линия располагается перпендикулярно к ней.

- если центр давления перемещается по прямой, не проходящей через центр тяжести сечения, то нейтральная линия будет поворачиваться вокруг некоторой точки.

На основании этих свойств, используя зависимости (2), можно получить ядро сечения, т.е. область очерченную вокруг центра тяжести сечения, обладающую тем свойством, что сила приложенная в пределах этой области вызывает по всему брусу напряжения одного знака. Знание положения ядра сечения необходимы на практике при проектировании конструкций изготовленных из хрупких материалов (например, бетонных фундаментов нефтехимических аппаратов), которые, как известно, хуже сопротивляются растяжению, чем сжатию. Поэтому для них необходимо предусматривать приложение сжимающих нагрузок только в пределах ядра сечения, чтобы в сечениях такой конструкции возникали только сжимающие напряжения.

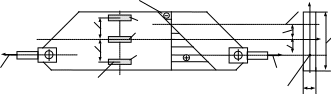
В проводимой лабораторной работе для выявления закона распределения нормальных напряжений в поперечном сечении внецентренно растянутого стержня используется специальное приспособление-образец типа СМ-2В, в виде стального бруса прямоугольного сечения с размерами 150х12 мм. Приспособление-образец крепится к захватам разрывной машины УММ-5 (описание машины приводилось в лабораторной работе № 1) и растягивается вдоль продольной его оси силой, линия действия которой смещена на величину эксцентриситета “е”, равного 30 мм (рисунок 1).

эпюра напряжений (s) у

нейтральная линия

с 3

2 у_н.л. х h

с е

1

F F

тензодатчики центр давления b

Рисунок 1- Схема нагружения образца и расположения тензодатчиков

Измерение напряжений выполняется методом тензометрирования (подробно описание этого метода приведено в лабораторной работе № 4), для чего на поверхность образца в продольном направлении наклеены три датчика электрического сопротивления, имеющих одинаковую базу и коэффициенты чувствительности. Расположение тензодатчиков показано на рисунке 1.

Измерение деформаций производится прибором ИД-70 по методике, подробно изложенной в лабораторной работе № 4.