7. Лекция 7. Программирование ключевых операций цос в matlab

Наиболее совершенным средством для реализации цифровой обработки данных в режиме off line является система MATLAB. В среде MATLAB есть также все необходимые программные средства для генерации модельных сигналов и управления аппаратурой.

Основные арифметические операции в MATLAB: сложение, вычитание, умножение , деление и возведение в степень. Операции умножения, деления и возведения в степень рассчитаны на работу с матрицами, поэтому при поэлементных операциях они записываются как .*, ./ и .^ (т.е. перед знаком операции ставится точка).

Основные операторы: присваивания, цикла и условия. Синтаксис основных операций – такой же, как в С/С++. Признак комментария знак % перед строкой.

Большой набор стандартных функций для работы с матрицами, для различных видов цифровой обработки, графического представления результатов.

Модельный синусоидальный сигнал x(k) амплитудой А, с количеством отсчетов N, количеством периодов KP может быть создан с помощью следующего фрагмента программы:

for k=1:N

x(k) = A*sin(2*pi*KP*k/N);

end

Понятие частоты у модельного сигнала отсутствует, длительность периода во времени также не определена. Длительность периода и частота становятся определенными только если задать шаг дискретности измерений во времени dt. В этом случае общее время измерения T_изм = N*dt, период сигнала T = N*dt/KP, частота f = KP/(N*dt).

Для создания массива нормально распределенного шума q с СКО = 1, содержащего N значений служит функция randn:

noise=randn(N)

для генерации «белого» Гауссова шума- функция wgn:

noise=wgn(N,1,А)

где N,1 – размерность массива шума,

А – мощность шума (Вт), А = 20lgK, К-масштабный коэффициент

Гауссов (нормально распределенный) шум. Плотность вероятности этого шума определяется выражением

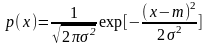
где 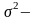дисперсия шума, m-его среднее значение.

Гауссовы процессы обладают характерным свойством: любой такой процесс полностью определяется своими статистическими характеристиками 1-го и 2-го порядка. Этим объясняется выбор гауссовых процессов в качестве гипотезы при расчетах, содержащих погрешности оценок и требующих вычисления моментов более высоких порядков. Кроме того, согласно центральной предельной теореме, сумма произвольных случайных процессов стремится к гауссову процессу при возрастании числа слагаемых. Сходимость оказывается настолько быстрой, что если число слагаемых больше 5 или 6, то результирующий процесс очень близок к гауссову.

Белый шум. Белым называют шум, спектральная плотность мощности которого постоянна по всему диапазону частот. Реально белый шум не существует; но если спектральная плотность шума постоянна внутри полосы частот, пропускаемых системой, то такой шум можно считать белым.

Базовые операции цифровой обработки реализуются с помощью следующих функций:

1. Линейная свертка (конволюция) выполняется с помощью функции conv, например:

X()=conv(x,h);

где x – массив обрабатываемого сигнала, содержащий N значений; h – массив импульсного отклика объекта, например, фильтра, содержащий М значений, M<N, X() – результат выполнения свертки, например, массив выходного сигнала фильтра.

2. Корреляция выполняется с помощью функции xcorr, например: W=xcorr(x,y);

где x, y – числовые массивы x и y, содержащие по N значений сигнала, X – числовой массив функции взаимной корреляции, содержащий 2*N значений.

Автокорреляция выполняется с помощью этой же функции, аргументом являются два одинаковые массива – x или y.

3. Фильтрация и функциональные преобразования выполняются с помощью нескольких функций. Для выполнения частотной фильтрации необходимо вычислить частотную характеристику или импульсный отклик фильтра и частотный спектр сигнала.

3.1. Частотный спектр Х() сигнала х(t) вычисляется с помощью функции быстрого преобразования Фурье fast fourie transform (БПФ, fft):

Х() =fft(x,N);

2. Импульсный отклик вычисляется с помощью обратного преобразования Фурье (ОБПФ, ifft) частотной характеристики фильтра, например:

h(t)=ifft(H())

2. Частотная характеристика фильтра в дискретизированном виде (в виде числового массива) вычисляется по аналогии с частотной характеристикой в непрерывной форме, например, для линейного фильтра:

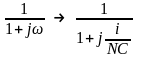
где i – номер элемента числового массива частотной характеристики,

NC - полоса пропускания фильтра по уровню 0,7 амплитуды

выражена в количестве отчетов спектра БПФ, пропускаемых

фильтром.

Фильтр может быть реализован с помощью следующего программного кода:

for i=1:N

H(i)=1/(1+j*i/NC);

end

2. Для того, чтобы вычислить выходной сигнал фильтра, нужно выполнить операцию свертки массива частотного спектра X() входного сигнала с частотной характеристикой фильтра H() с помощью функции обратного преобразования Фурье:

Z()= Х().*H()

z(t)=ifft(X().*H());

или операции свертки массива входного сигнала с импульсным

откликом фильтра, например:

z(t) = conv(x(t),h(t)).

Приведенные две формы вычисления выходного сигнала фильтра основаны на теореме Планшереля [Ж.Макс Методы и техника обработки сигналов при физических измерениях. Т.1. М.:Мир, 1983, 305С.]. Теорема Планшереля утверждает, что преобразование Фурье свертки двух функций, равно произведению изображений (в частотной области (В.С.)) функций, составляющих свертку, и наоборот. Т.е. справедливо соотношение:

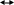x(t)*h(t) X()H()

Здесь знак * обозначает операцию свертки. На языке функций MATLAB соотношение, основанное на теореме Планшереля, запишется так :

fft(conv(x(t),h(t)) = X().*H()

Здесь знак * обозначает операцию умножения, а операция свертки записывается с помощью функции conv.

3.5. Для реализации оптимального фильтра Колмогорова-Винера требуется вычисление энергетического спектра (плотности мощности) сигнала и шума. Для этого предусмотрена функция conj умножения массива комплексных чисел на массив комплексно сопряженных чисел, например:

S=X().*conj(X())/N;

где X() – массив частотного спектра, полученный с помощью функции fft (БПФ);

N – количество элементов массива частотного спектра сигнала или шума;

S – массив частотного спектра мощности сигнала или шума.

6. Для реализации фильтров Баттерворта, Чебышева и др. предусмотрены также более простые средства. Например, фильтр Баттерворта может быть реализован с помощью следующего программного кода:

n=4;%порядок фильтра

[b a]=butter(n, 0.5);%0.5-относительная частота среза

y=filter(b,a,x);

Ниже приведена программа фильтрации сигналов с помощью низкочастотного фильтра.

%Низкочастотный фильтр

A=20; %амплитуда сигнала

Q=5; %амплитуда шума

KP1=12;% - количество периодов первого сигнала

N=1024;%количество точек расчета

NC=12; %NC - полоса пропускания фильтра по уровню 0,7 %амплитуды,выраженная в количестве отчетов спектра БПФ, %пропускаемых фильтром

% остальные отсчеты (в частотном спектре!) будут %ослабляться по амплитуде

for k=1:N % генерация сигнала и шума

s(k) = A*sin(2*pi*KP1*k/N);

q(k)=Q*(randn(N)); %шум

x(k)=s(k)+q(k); % суммирование сигнала и шума

end

Y=fft(x,N)/N; %БПФ сигнала с шумом

for i=1:N

H(i)=1/((1+j*i/NC)); %передаточная функция простого фильтра

%в частотной области

end

i=1:400;

i=1:N;

X1=fft(x,N); %частотный спектр сигнала с шумом

Z=ifft(X1.*H); %свертка зашумленного сигнала с частотной хар-кой фильтра

Построение и оформление графиков в MATLAB

i=1:N;

y=A*sin(6.28*KP*i/N); %создание N значений KP периодов модельного sin %сигнала,

figure %создание окна графического вывода

%plot(i,y(1:50));%вывод графика y, кол-во точек – 50.

%plot(i,y) ;% вывод графика y (все N точек)

%plot (i,2*y(1:N),’r-’);%отображение графика y линией красного цвета

%semilogx(i,abs(y(1:200))),grid; %то же, что и plot, но в логарифмическом

% масштабе по Х

%loglog(i,abs(y(1:200))); % в логарифмическом масштабе по Х и Y

grid on; %отображение линий координатной сетки

%title(‘сигнал до фильтра’);%заголовок графика

xlabel(‘номер отсчета’); % подпись по оси Х

ylabel(‘амплитуда’); % подпись по оси Y

legend(‘до фильтра’);%подпись легенды

axis tight; %диапазон Х и Y по осям точно соответствует Xmax и Ymax %(автомасштабирование)

hold on; % «удержание» окна вывода для следующего графика

hold off; %отмена «удержания»

close all; %закрытие всех открытых окон графического вывода