
- •Лекция 1. Цос. Введение
- •Лекция 2. Разложение функций в ряды Ортонормированный базис
- •Лекция 3. Математическое представление сигнала. Методы исследования подобия сигналов. Корреляция.
- •Лекция 5. Разложение функций в комплексный ряд фурье
- •Лекция 6. Ключевые операции цос
- •Лекция 7. Программирование ключевых операций цос в matlab
- •Лекция 8. Цифровая фильтрация
- •Лекция 9. Оптимальная и согласованная фильтрация
- •Лекция 10. Применение цос для обработки коротких сигналов. Оконная фильтрация
- •Лекция 11. Цифровая обработка коротких сигналов. Определение частоты сигнала.
- •Алгоритм определения частоты
- •Лекция 13. Цифровая обработка нестационарных сигналов. Преобразование гильберта-хуанга. Введение
- •Лекция 14. Преобразование гильберта
- •Лекция 15. Обработка изображений. Введение.
- •Лекция 16. Методы улучшение визуального качества изображений
- •Улучшение качества изображения путем выравнивания гистограммы
- •Улучшение качества изображения с помощью гамма-коррекции
- •Лекция 17. Средства идентификации объектов на изображениях
- •Определение порога принятия решения по принципу максимума правдоподобия
- •Лекция 18. Основы проектирования систем цос.
- •Выбор ацп.
Лекция 3. Математическое представление сигнала. Методы исследования подобия сигналов. Корреляция.
Методы цифровой обработки обоснованы в [1] на основе аналогии с векторным представлением дискретизированных сигналов. Изложение этого подхода приведено ниже.
При малом интервале дискретизации можно достаточно точно воспроизвести аналоговый сигнал по цифровому сигналу. Если временной интервал [a,b] разделить на одинаковые отрезки, а сигнал f, уже подвергшийся дискретизации, перевести в цифровую форму и записать в виде ряда значений N точек
f=(f1, f2, …fN),
то f можно представить N-мерным вектором (N-мерным вектором называется величина, представленная набором N числовых значений, расположенных в определенном порядке). Элемент из этого числового набора называется компонентом вектора.
Качество приближения функции f(t) будет зависеть от числа N. Если увеличивать N, то степень приближения будет тоже увеличиваться. Если увеличивать N до бесконечности, то вся информация, содержащаяся в f(t), будет содержаться в f. Это означает, что анализ вектора f аналогичен анализу функции непрерывного сигнала f(t), если она не имеет точек разрыва.
Двумерный вектор соответствует одной точке в двумерном пространстве, т.е. на плоскости, трехмерный вектор тоже соответствует одной точке, но в трехмерном пространстве, а N-мерный вектор – одной точке в N-мерном пространстве. Назовем это пространство бесконечно большой размерности пространством функций.
Цель этой аналогии заключается в том, чтобы объяснить физический смысл коэффициента корреляции как показателя степени близости функций, и прицип разложения любой произвольной функции сумму составляющих (это объяснит, например, почему возможно разложение любой функции в ряд Фурье или какой-либо другой и по каким функциям можно разложить, а по каким нельзя).
Для этого необходимо определить понятия: расстояния между векторами, скалярное расстояние, норма вектора.
Определение степени близости функций
Рассмотрим задачу определения взаимоотношения между сигналами f(t) и g(t) по их векторному представлению. Конечно, два значения сигнала весьма слабо характеризуют сигналы, но, как будет показано дальше, выводы, сделанные по двум выборкам могут быть распространены на случай сколь угодно большого количества выборок.
Итак, определим векторы, содержащие по два элемента из выборки каждого сигнала, иначе говоря, двумерные векторы. Обозначим их как f и g:
 f=(
f1
, f2),
g=(
g1
, g2
)
f=(
f1
, f2),
g=(
g1
, g2
)
Если сигналы выразить через векторы, то исследование отношений между сигналами будет равносильно исследованию отношений между векторами. Исследование может заключаться в определении степени близости функций. В векторном представлении это соответствует расстоянию между векторами. Обозначим d(f,g) расстояние между векторами f и g. Чем меньше значение d, тем ближе векторы f и g, а, значит, и сильнее между ними взаимосвязь.
Величину вектора f (абсолютное значение) обозначим как || f ||. Используя компоненты вектора f, получим:
![]()
|| f || называют также нормой вектора f.
Итак, из рис. 1 видно, что расстояние между векторами f и g есть норма вектора f – g. Это можно записать, используя компоненты векторов, в следующем виде:
![]()
Однако, норма вектора характеризует лишь величину вектора разности, но не учитывает его направления.
Для выражения
связи между векторами используют
скалярное произведение. Скалярное
произведение между f
и g
обозначается как
![]() и определяется как
и определяется как
![]()
Следовательно

![]()
О бозначим
эту величину
бозначим
эту величину
 ,
следовательно
,
следовательно

Величина r
выражает силу связи между векторами f
и g
через угол между ними. Если направления
f
и g
совпадают, т.е.
 ,
то r
принимает максимальное значение, равное
1. С увеличением угла
,
то r
принимает максимальное значение, равное
1. С увеличением угла
 значение r
уменьшается. Если r=0,
т.е.
значение r
уменьшается. Если r=0,
т.е.
![]() =0,
то векторы f
и g
взаимно
перпендикулярны. Назовем величину r
коэффициентом
корреляции.
=0,
то векторы f
и g
взаимно
перпендикулярны. Назовем величину r
коэффициентом
корреляции.
Как видно из приведенного выше соотношения, r зависит от угла между векторами и не зависит от нормы векторов. Выразим скалярное произведение, используя компоненты вектора:
![]()
Чтобы вывести эту формулу, применим теорему косинусов для векторов:

Следовательно

Подставим полученные результаты в выражение коэффициента корреляции и представим r следующим образом:

Представляя это выражение через составляющие вектора, получим
Из этого соотношения можно вывести выражение для коэффициента корреляции в N-мерном пространстве:

Обобщив
последнее соотношение можно вывести
формулу для скалярного произведения
функций. Используя соответствие вектор
![]() функция, сумма
интеграл, определим скалярное произведение
функций f(t)
и g(t)
на интервале [a,b]
:
функция, сумма
интеграл, определим скалярное произведение
функций f(t)
и g(t)
на интервале [a,b]
:

Скалярное произведение функции f(t) на саму себя:
![]()
Это означает, что f(t) имеет те же свойства, какими обладает многомерный вектор в векторном пространстве. То, что мы смогли определить скалярное произведение функций, означает также и то, что мы приняли и учли такое понятие, как угол между функциями. Если функции f(t) и g(t) в пространстве функций расположены под углом , то коэффициент корреляции можно определить так же, как и в случае векторов, используя норму и скалярное произведение:

Если записать подробно, то получим:

Это соотношение имеет довольно сложный вид, но принцип тот же, что и в случае векторов. Как и прежде, коэффициент корреляции показывает степень «похожести» функций. Причем r принимает значения от -1 до 1. Чем больше значение r по абсолютной величине, тем выше корреляция между функциями. Иначе говоря, они более похожи.
Однако стоит отметить, что коэффициент корреляции не является единственным показателем похожести функций.
ЛЕКЦИЯ 4. РАЗЛОЖЕНИЕ ФУНКЦИЙ В ДЕЙСТВИТЕЛЬНЫЙ РЯД ФУРЬЕ
Раньше было показано, что любую функцию f(t) можно представить в виде:

где
 - ортонормированные функции.
- ортонормированные функции.
Коэффициенты сk вычисляются по формуле:

Условие ортонормированности выполняется, если скалярное произведение любых двух функций, входящих в набор, равно нулю, а норма любой функции равна единице:

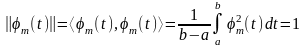
Разложение
функции на интервале
![]()
Функцию f(t) можно разложить по системе тригонометрических функций на отрезке следующим образом:

Коэффициенты
![]() ,
как было показано ранее, можно выразить
через скалярные произведения:
,
как было показано ранее, можно выразить
через скалярные произведения:
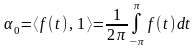


В общем виде функцию f(t) можно представить следующим образом:

Коэффициенты
![]() называют коэффициентами Фурье, а
подобное представление функции
называется разложением в ряд Фурье.
Иногда такое представление называют
действительным разложением в ряд Фурье,
а коэффициенты — действительными
коэффициентами Фурье. Термин
«действительный» вводится для того,
чтобы отличить представленное разложение
от разложения в ряд Фурье в комплексной
форме, о котором мы будем говорить позже.
Как уже было сказано раньше, произвольную
функцию можно разложить по системе
ортогональных функций, даже если
функции из этой системы не представляются
в виде тригонометрического ряда. Обычно
под разложением в ряд Фурье подразумевается
разложение в тригонометрический ряд.
Если коэффициенты Фурье выразить через
,
получим:
называют коэффициентами Фурье, а
подобное представление функции
называется разложением в ряд Фурье.
Иногда такое представление называют
действительным разложением в ряд Фурье,
а коэффициенты — действительными
коэффициентами Фурье. Термин
«действительный» вводится для того,
чтобы отличить представленное разложение
от разложения в ряд Фурье в комплексной
форме, о котором мы будем говорить позже.
Как уже было сказано раньше, произвольную
функцию можно разложить по системе
ортогональных функций, даже если
функции из этой системы не представляются
в виде тригонометрического ряда. Обычно
под разложением в ряд Фурье подразумевается
разложение в тригонометрический ряд.
Если коэффициенты Фурье выразить через
,
получим:

Поскольку при k = 0 cos(kt) = 1, то константа a0/2 выражает общий вид коэффициента ak при k = 0.


В последнем соотношении колебание самого большого периода, представленное суммой cost и sint, называют колебанием основной частоты или первой гармоникой. Колебание с периодом, равным половине основного периода, называют второй гармоникой. Колебание с периодом, равным 1/3 основного периода, называют третьей гармоникой и т.д. Как видно из соотношения (5.1) а0 является постоянной величиной, выражающей среднее значение функции f(t). Если функция f(t) представляет собой электрический сигнал, то а0 представляет его постоянную составляющую. Следовательно, все остальные коэффициенты Фурье выражают его переменные составляющие.
Первая гармоника является периодической функцией с периодом 2. Прочие гармоники также имеют период, кратный 2. Исходя из этого, при формировании сигнала из составляющих ряда Фурье мы, естественно, получим периодическую функцию с периодом 2. А если это так, то разложение в ряд Фурье — это, собственно говоря, способ представления периодических функций.
Итак, каждая из
гармоник, представленных рядом Фурье,
представляет собой сумму вида
a*cos(x)+b*sin(x).
Эта сумма может быть преобразована к
виду
 :
:
Лемма. Если сумма квадратов двух действительных чисел равна единице, то одно из этих чисел можно рассматривать как косинус, а другое как синус некоторого угла.
Другими словами, если а2 + b2 = 1, то существует угол φ, такой, что
а = cos φ; b = sin φ.
Прежде чем доказывать эту лемму, поясним ее на следующем примере:
( \/3/2 )2 + ( 1/2 )2 = 3/4 + 1/4 = 1
Поэтому существует угол φ, такой, что \/3/2 = cos φ; 1/2 = sin φ.
В качестве φ в данном случае можно выбрать любой из углов 30°, 30° ± 360°, 30° ± 2 • 360° и т. д.
Доказательство леммы.
Рассмотрим вектор 0А с координатами (а, b). Поскольку а2 + b2 = 1, длина этого вектора равна 1. Но в таком случае его координаты должны быть равны cos φ и sin φ, где φ — угол, который образует данный вектор с осью абсцисс. Итак, а = cos φ; b =sin φ, что и требовалось доказать. |
|
Доказанная лемма позволяет преобразовать выражение a sin х + b cos х к более удобному для изучения виду.
Прежде всего вынесем за скобки выражение \/ а2 + b2

Поскольку
![]()
первое из чисел
![]() и
и
![]() можно рассматривать как
косинус некоторого угла
φ ,
а второе как синус того же угла φ:
можно рассматривать как
косинус некоторого угла
φ ,
а второе как синус того же угла φ:
![]()
Но в таком случае
a sin
х
+ b
cos х
=
![]() ( cos φ sin
х
+ sin φ cos
х)
=
sin
( x + φ
)
( cos φ sin
х
+ sin φ cos
х)
=
sin
( x + φ
)
Итак,
a sin х + b cos х = sin ( x + φ ) , где угол φ определяется из условий
![]()
Разложение
функции, представленной в дискретизированном
виде, в ряд Фурье на интервале

В дискретизированном виде (т.е. в виде набора дискретных значений или, что то же, в виде числового массива, содержащего N значений) функция f(t) на интервале будет иметь вид:

где
N
– количество дискретных значений
сигнала. При
 дискретизированная функция будет
приближаться к непрерывной f(t).
дискретизированная функция будет
приближаться к непрерывной f(t).
Разложение в ряд Фурье будет иметь вид, аналогичный тому, который был получен для случая непрерывного сигнала:
а
коэффициенты
 :
:
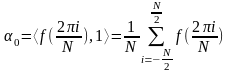 ;
;
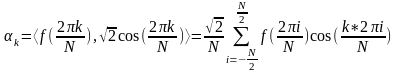 ;
;
 .
.
и коэффициенты a0, ak и bk:



а общий вид разложения:
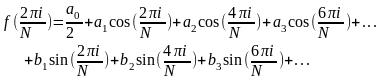
Ниже
приведена программа вычисления
коэффициентов разложения для функции
y(t)=t
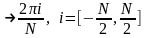 .
.
% Разложение функции t3 в ряд Фурье
%в
дискретизированном виде на интервале

N=255; %Количество отсчетов (элементов массива y(t))
K=16; %Количество членов ряда Фурье
T=pi; %диапазон изменения функции f(i) равен +/-T
kp=2.4; %количество периодов гармонической функции
y=zeros(1,N+1);
Sa = zeros(1,K);
Sb = zeros(1,K);
p=3;% показатель степени функции t^p
f=zeros(1,N+1);
Sa0=0;
for i=1:N+1
f(i)=sin(2*pi*kp*(i-1)/N); % гармоническая функция
% f(i)= (2*T*(((i-1-N/2))/N))^p; %функция t^p
Sa0=Sa0+f(i);
end
Sa0=Sa0/N
for i=1:N+1
for j=1:K
Sa(j) = (Sa(j)+f(i)*cos((j)*2*pi*(i-1-N/2)/N));
Sb(j) = (Sb(j)+f(i)*sin((j)*2*pi*(i-1-N/2)/N));
end
end
for j=1:K
Sa(j)=Sa(j)*(1/(N/2));
Sb(j)=Sb(j)*(1/(N/2));
end
%Вычисление и отображение спектра амплитуд (начало)
for j=1:K
Sab(j)=sqrt(Sa(j)^2+Sb(j)^2);
end
i=1:K;
figure
plot(i,Sab);
stem(Sab(1:K)); %вывод графика дискретной последовательности данных
axis([1 8 -0.2 1.2]);%задание осей: [xmin xmax ymin ymax]
title('Амплитуды частотных составляющих спектра');
xlabel('Количество периодов')
axis tight;
%Вычисление и отображение спектра амплитуд (конец)
y=zeros(1,N+1);
for i=1:N+1
for j=1:K
y(i)= y(i)+Sa(j)*cos(j*2*pi*(i-1-N/2)/N)+Sb(j)*sin(j*2*pi*(i-1-N/2)/N);
end
y(i)=Sa0+y(i);
end
i=1:N+1;
figure
plot(i,f);
axis tight;
hold on;
plot(i,y,'r-')
hold off;
pause;close all;

Рис. 1. Исходная и восстановленная функция t3 при N=128, K=32,p=3.
Примечание. Для разложения четной функции из ряда можно исключить члены, содержащие синусы, для разложения нечетной – косинусы. Но можно оставить ряд разложения полностью.
Разложение функции на интервале [-T/2,T/2]
До этого момента мы рассматривали функцию переменной t на отрезке [-,]. В случае периодического сигнала с периодом 2 мы брали этот интервал за основной. В общем случае периодического сигнала с периодом Т при разложении в ряд Фурье мы должны использовать интервал [-Т/2, Т/2]. Если интервал [-,] расширить (или сократить) до интервала [-T/2, Т/2], то и период первой гармоники увеличится (или уменьшится) от 2 до Т. Поскольку кратность этого преобразования равна (Т/2), то составляющие первой гармоники примут вид:

Для составляющих k-й гармоники можно записать:

Следовательно, если функцию f(t) разложить в ряд Фурье на интервале [-Т/2, Т/2], получим:

Если обозначить
угловую частоту через
 ,
то поскольку
,
то поскольку
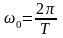 ,
последнее выражение можно записать и
в таком виде:
,
последнее выражение можно записать и
в таком виде:

В соотношении, определяющем коэффициенты Фурье на отрезке

произведем замену переменной
![]()
а также замену отрезка, на котором берется интеграл
![]()
Оставив функцию f(t) без изменения, получим

Аналогичным образом выводится следующее соотношение:

Разложение функции, представленной в дискретизированном виде, в ряд Фурье на интервале [-T,T]
В дискретизированном виде (т.е. в виде набора дискретных значений или, что то же, в виде числового массива, содержащего N значений) функция f(t) на интервале [-T,T] будет иметь вид:

где N – количество дискретных значений сигнала. При дискретизированная функция будет приближаться к непрерывной f(t).
Разложение в ряд Фурье будет иметь тот же вид, что и при разложении функции в непрерывной форме, а коэффициенты :
 ;
;
 ;
;
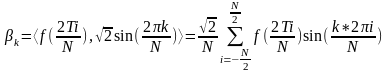 .
.
и коэффициенты a0, ak и bk:



а общий вид разложения:

Ниже
приведена программа вычисления
коэффициентов разложения для функции
y(t)=t
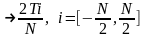 .
.
% Разложение функции y(t)=tp в ряд Фурье
%
в дискретизированном виде на интервале
[0,T],
например,
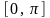
N=255; %Количество отсчетов (элементов массива y(t)=t)
K=64;%Количество членов ряда Фурье
T=pi;%диапазон изменения функции f(i)+/-T
kp=2.0
y=zeros(1,N+1);
Sa = zeros(1,K);
Sb = zeros(1,K);
p=3;%показатель степени функции t^p
f=zeros(1,N+1);
Sa0=0;
for i=1:N+1
f(i)=sin(2*pi*kp*(i-1)/N); % гармоническая функция
% f(i)= (T*(((i-1))/N))^p; %функция t^p, i-1, если p>0, i, если p<0
Sa0=Sa0+f(i);
end
Sa0=Sa0/N
for i=1:N+1
for j=1:K
Sa(j) = (Sa(j)+f(i)*cos((j)*2*pi*(i-1)/N));
Sb(j) = (Sb(j)+f(i)*sin((j)*2*pi*(i-1)/N));
end
end
for j=1:K
Sa(j)=Sa(j)*(1/(N/2));
Sb(j)=Sb(j)*(1/(N/2));
end
%Вычисление и отображение спектра амплитуд (начало)
for j=1:K
Sab(j)=sqrt(Sa(j)^2+Sb(j)^2);
end
i=1:K;
figure
plot(i,Sab);
stem(Sab(1:K)); %вывод графика дискретной последовательности данных
axis([1 8 -0.2 1.2]);%задание осей: [xmin xmax ymin ymax]
title('Амплитуды частотных составляющих спектра');
xlabel('Количество периодов')
axis tight;
%Вычисление и отображение спектра амплитуд (конец)
y=zeros(1,N+1);
for i=1:N+1
for j=1:K
y(i)= y(i)+Sa(j)*cos(j*2*pi*(i-1-N)/N)+Sb(j)*sin(j*2*pi*(i-1-N)/N);
end
y(i)=Sa0+y(i);
end
i=1:N+1;
figure
plot(i,f);
axis tight;
hold on;
plot(i,y,'r-')
hold off;
pause;
close all;

Рис. 2. Исходная и восстановленная функция y=tp после разложения в ряд Фурье, N=128, T=5, p=4,K=16.

