4. Законы сохранения в механике

4.1. Закон сохранения полной механической энергии

Полная механическая энергия системы тел равна сумме их кинетической и потенциальной энергии взаимодействия этих тел друг с другом и с внешними телами:

Е = Е_к + Е_п.

Приращение механической энергии системы определяется работой всех неконсервативных сил (внешних и внутренних):

.

Закон сохранения полной механической энергии: Полная механическая энергия системы тел, на которые действуют только консервативные силы, остается постоянной.

В замкнутой системе полная механическая энергия остается постоянной, если между телами, составляющими систему, действуют только консервативные силы.

4.2. Закон сохранения импульса. Центральный удар двух тел

Закон сохранения импульса: Полный импульс замкнутой системы остается посто­янным.

Для замкнутой системы будут сохраняться и проекции импульса на координатные оси:

.

Если 0, но =0, то будет сохраняться проекция импульса системы на ось Х.

Рассмотрим центральный удар двух тел. Центральным называется удар, при котором тела движутся вдоль прямой, соединяющей их центры масс. Выделяют два предельных вида такого удара: абсолютно упругий и абсолютно неупругий.

Для двух тел массами m₁ и m₂ , движущихся со скоростями ивдоль оси X навстречу друг другу, скорости их после абсолютно упругого центрального удара можно найти по формулам

; .

При этом сохраняется импульс системы тел и полная механическая энергия.

Если удар абсолютно неупругий, то

.

Тела после такого удара движутся вместе. Импульс системы тел сохраняется, а полная механическая энергия не сохраняется. Часть механической энергии переходит в энергию неупругой деформации и во внутреннюю энергию тел.

4.3. Закон сохранения момента импульса

Закон сохранения момента импульса: Момент импульса системы тел сохраняется, если результирующий момент внешних сил, действующих на систему, равен нулю:

.

Если результирующий момент внешних сил не равен нулю, но равна нулю проекция этого момента на некоторую ось, то проекция момента импульса системы на эту ось не изменяется.

5. Элементы специальной теории относительности

5.1. Постулаты Эйнштейна. Преобразования Лоренца

Принцип относительности: никакими физическими опытами, производимыми внутри инерциальной системы отсчета, невозможно установить, покоится ли эта система относительно другой инерциальной системы отсчета или движется прямолинейно и равномерно.

Принцип постоянства скорости света: скорость света в вакууме одинакова во всех инерциальных системах отсчета и не зависит от движения источников и приемников света.

Рассмотрим две системы отсчетаS и S (рис. 8). Систему S будем считать условно неподвижной. Система движется относительносо скоростьювдоль оси X системы. Для перехода от одной системы отсчета в другую в специальной теории относительности используютсяпреобразования Лоренца.

Пусть в начальный момент времени начала координат обеих систем и направления соответствующих осей совпадают.

Рис. 8

Тогда:

Здесь - скорость света в вакууме.

5.2. Следствия из преобразований Лоренца

Будем рассматривать системы и(рис. 8).

Относительность промежутков времени между событиями.

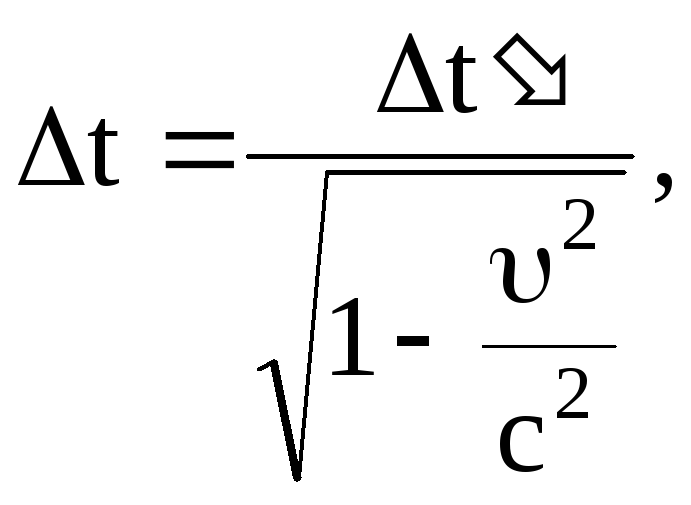
где - промежуток времени между событиями, измеренный в системе отсчета, относительно которой события происходят в одной точке пространства (отсчитывается по часам, находящимся в системе);- промежуток времени между этими событиям, отсчитанный по часам, находящимся в системе.

Изменение размеров движущихся тел.

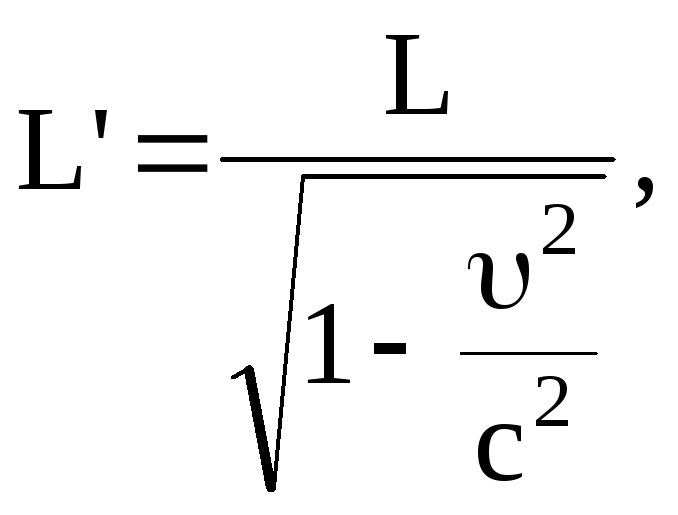
где L′ -длина стержня, расположенного вдоль оси и покоящегося в системеS’ (отсчитывается в системе отсчета S’); L - длина этого же стержня, измеренная в системе отсчета .

Релятивистский закон сложения скоростей.

Пусть некоторое тело движется вдоль оси x′ в системе отсчета со ско­ростьюотносительно последней. Найдем проекцию скоростиэтого тела в систе­ме отсчетана ось x этой системы:

3. Релятивистские масса и импульс. Взаимосвязь массы и энергии

Эйнштейн показал, что масса тела зависит от его скорости:

где m₀ – масса тела в той системе отсчета, относительно которой тело покоится (масса покоя);

m – масса тела в той системе, относительно которой тело движется;

 – скорость тела относительно системы отсчета, в которой определяется масса m.

Релятивистский импульс

,

где m – релятивистская масса.

Закон взаимосвязи массы и энергии:

,

где E – полная энергия материального объекта; m - релятивистская масса.

Кинетическая энергия объекта:

,

где - полная энергия;- энергия покоя.

Из закона взаимосвязи массы и энергии следует, что всякое изменение массы тела на m сопровождается изменением его энергии на E:

E=mc².