Статическое решение для схемы на рис. 1
Как следует из рассмотрения предыдущей задачи для одного контура, если в полной схеме на рис. 1 разности потенциалов источников тока являются неизменными во времени, то через некоторое время после включения (определяемого временами зарядки конденсаторов), заряды на конденсаторах не будут меняться и «токи через конденсаторы перестанут протекать». Другими словами можно считать, что к уравнениям (1)-(7) следует добавить условия равенства нулю левых частей уравнений (6)-(7) Эти условия приведут к тому, что
(18)
В этом случае сумма уравнений (1)+(3)+(4) приводит к ожидаемому равенству
, (19)
разность узловых потенциалов определяются уравнениями (1) и (4):
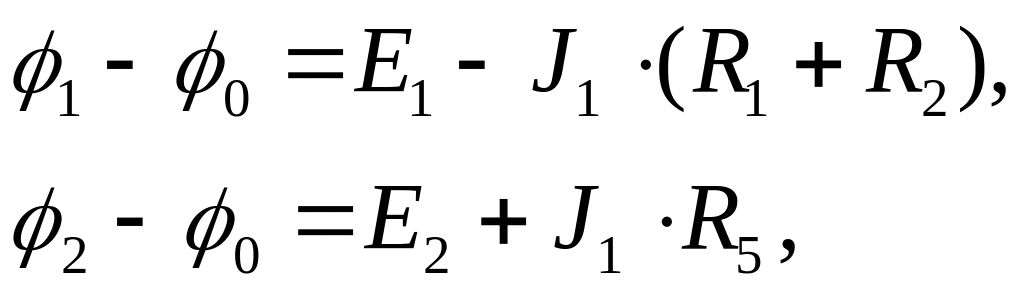(20)
а заряды конденсаторов определяются уравнениями (2) и (5):
(21)
Рис 3. Схема для рассмотрения статического решения при постоянных значениях E1 и E2.
Динамика зарядов на конденсаторах в общем случае уравнений (1)-(7)
Систему уравнений (1)-(7) нетрудно записать в матричном виде. Такая запись является более наглядной и позволяет легче охватить общую структуру уравнений, а также сформулировать общую постановку задачи и пути ее решения.
Введем необходимые обозначения. Объединим
в один вектор
две известные величины
,
а семь неизвестных величин представим
в виде двух векторов
и
.
В первый вектор
включим два неизвестных заряда
и во второй вектор
- оставшиеся пять неизвестных величин
- три тока и две разности потенциалов:
(22)
Нам потребуются еще три прямоугольные
матрицы, состоящие из постоянных величин
и обозначенных большими греческими
буквами
:
одна матрица размерности 2х5
, (23)
и две матрицы размерности 5х2
. (24)
И последняя (по счету, а не по значению) из необходимых нам матриц будет квадратная матрица 5х5, определяемая левой частью уравнений (1)-(5):
. (25)
Нетрудно проверить, что с помощью введенных обозначений исходная система уравнений (1)-(7) приобретет компактный вид:
(26)
Из (26) следует, что если матрица
не особая (т.е. обратима), то вся задача
может быть сведена к решению системы
двух линейных дифференциальных уравнений
для неизвестных зарядов на обкладках
двух конденсаторов:
(27)
С помощью MathCad можно вычислить определитель матрицы в символьном виде:
и, следовательно, в рассматриваемой задаче матрица обратима.
Заметим, что все матрицы в (27) не содержат
зависящих от времени величин. Поэтому
второе уравнение в (27) является неоднородным
векторным дифференциальным уравнением
с постоянными коэффициентами, в котором
зависимость правой части от времени
определяется зависимостью от времени
потенциалов источников токов
.
Общее решение этой задачи при любых
начальных условиях известно из стандартных
курсов по дифференциальным уравнениям.
Напомним, что определяющую роль в
поведение решения вектора
играют собственные значения матрицы
.
В дальнейшем мы обсудим методы решения
подобных задач отдельно.