К лекциям 1-2. Математическое моделирование электрических схем Введение

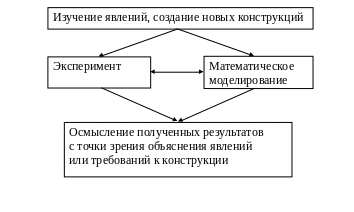
Обобщенно можно сказать, что физики и инженеры рассматривают процессы (явления) либо для их изучения, либо для создания новых конструкций и приборов.

Для обеих целей важнейшим этапом рассмотрения является эксперимент. Без него нельзя обойтись. Но можно несколько облегчить задачу изучения процессов созданием адекватной математической модели явления или конструкции.

Этапы эксперимента

1. Создание экспериментальной установки (конструкции).

2. Изменение параметров при проведении эксперимента

3. Выделение процессов, играющих основную роль в рассматриваемой области параметров.

Этапы математического моделирования

1. Построение математической модели на основе знаний об элементарных физических (химических, биологических, …) процессах, играющих основную роль в наблюдаемых явлениях.

2. Приведение модели к набору стандартных математических задач. При этом используется библиотека стандартных задач, известных исследователям.

3. Уточнение условий, когда рассматриваемые задачи имеют решения и когда оно единственно.

4. Выбор алгоритма решения.

5. Получение, если возможно, аналитическое решение.

6. Получение численных решений.

Иллюстрация возникновения разных математических задач

Рассмотрим задачи, которые возникают при математическом моделировании электрической схемы, представленной на рис. 1. Оказывается, что в зависимости от предположений о заданной зависимости ЭДС от времени можно получить разные математические задачи.

Рис.1 Схема, содержащая два ключа , два источника ЭДС E1, E2, семь сопротивлений R1-R7 и два конденсатора емкостью C1, C2.

В рассматриваемой схеме существуют три узловые точки (жирные точки на рис.1), в которых число входящих и исходящих токов больше двух. Мы обозначили потенциалы в этих точках буквами ф0, ф1, ф2. Необходимо написать соотношения между разностями этих потенциалов и протекающими токами по всем возможным путям прохождения тока между узловыми точками (что эквивалентно второму закону Кирхгофа).

Напомним факты, известные из курса физики. Ток , протекающий через сопротивление , связан с разностью потенциалов на концах сопротивления соотношением . Связь между током и разностью потенциалов на обкладках конденсатора более сложная и представлена на рис 2.

Рис. 2. Процесс зарядки конденсатора. Связь между током, зарядом и разностью потенциалов на обкладках конденсатора.

При рассмотрение электрических схем можно произвольно вводить неизвестные токи. Надо только придерживаться следующих правил.

1. Количество токов должно соответствовать числу независимых замкнутых ячеек схемы.

2. В каждой узловой точки сумма входящих и выходящих токов (с учетом знаков) должна равняться нулю (первый закон Кирхгофа).

На рис1. мы воспользовались тремя токами (по числу трех независимых контуров), обозначенных (нумерация привязана для удобства к номерам соответствующих сопротивлений, по которым эти токи протекают).

Нетрудно заметить, что между потенциалами ф0 и ф1 существуют два пути для токов . Для этих путей связь между разностью потенциалов и токами выражаются уравнениями (1), (2). Между узловыми точками с потенциалами ф1 и ф2 существует лишь один путь для тока , что и описывается соотношением (3). Для двух возможных путей протекания токов и между узловыми точками с потенциалами ф2 и ф0 связи между разностями потенциалов в узловых точках и протекающими токами определяются соотношениями (4), (5).

Связь между зарядами обкладок конденсатора и «протекающим» током определяются, согласно рисунку 2, дифференциальным соотношением между током и зарядом:

Таким образом, рассматриваемая электрическая схема эквивалентна системе пяти линейных алгебраических уравнений (1)-(5) и двух линейных дифференциальных уравнений (6)-(7) для семи величин: двух разностей между узловыми потенциалами (ф1-ф0), (ф2-ф0), трех токов и зарядов на обкладках двух конденсаторов.

В общем случае, когда разности потенциалов у источников ЭДС известны как заданные функции времени, то и все семь искомых величин будут также функциями времени. В этом случае если мы зададим для них начальные условия, то получим математическую задачу, известную в математике как задача Коши.