2. Линейные дифференциальные уравнения высшего порядка с постоянными коэффициентами

Определение. Линейным дифференциальным уравнением n-го порядка с постоянными коэффициентами называется уравнение вида

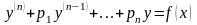, (27)

где 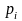, 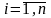- некоторые постоянные.

Определение. Уравнение

(28)

называется характеристическим уравнением для дифференциального уравнения (27).

Общее решение однородного линейного дифференциального уравнения с постоянными коэффициентами

Определение. Однородным линейным дифференциальным уравнением n-го порядка с постоянными коэффициентами называется уравнение вида

, (29)

где , - некоторые постоянные.

Если характеристическое уравнение для уравнения (29) имеет корни , , тогда

1. каждому -кратному действительному корню характеристического уравнения (29) соответствует частных решений вида , ,…, ;

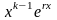2. каждой паре -кратных комплексно сопряженных корней характеристического уравнения (29) соответствует частных решений вида

, ,…, ,

, ,…, .

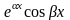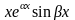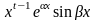Общая сумма кратностей всех корней должна равняться степени характеристического уравнения , поэтому число всех частных решений будет в точности совпадать с порядком уравнения.

Чтобы найти общее решение заданного уравнения, нужно взять линейную комбинацию указанных частных решений.

Пример 9. Решить уравнение .

Решение. Характеристическое уравнение имеет вид:

.

Корни этого уравнения , .

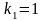Тогда общее решение данного уравнения:

.

Ответ: .

Пример 10. Решить уравнение

.

Решение. Характеристическое уравнение

.

Методом подбора найдем, что один из корней 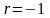, разделим многочлен на 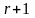, получим:

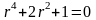или .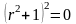

Корни этого уравнения , .

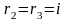Поэтому общее решение заданного дифференциального уравнения запишется в виде:

.

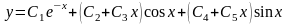Ответ: .

Общее решение неоднородного линейного дифференциального уравнения с постоянными коэффициентами

Уравнение вида (27), в котором правая часть не является тождественным нулем называют неоднородным дифференциальным уравнением с постоянными коэффициентами.

Справедлива теорема о структуре общего решения неоднородного уравнения (27): Общее решение уравнения с правой частью (27) можно составить как сумму общего решения соответствующего однородного уравнения и какого-либо частного решения данного уравнения.

Оказывается, что частное решение уравнения (27), где правая часть

,

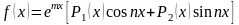имеет вид

,

где 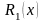, - многочлены степени, равной высшей из степеней многочленов 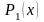, , 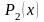а - кратность, с которой входят в число корней характеристического уравнения. Если не являются корнями характеристического уравнения, то принимаем равным нулю.

Пример 11. Решить уравнение .

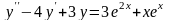Решение. Общее решение соответствующего однородного уравнения было найдено в примере 9 и имеет вид:

.

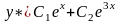Так как величина (коэффициент при в степени второй экспоненты в правой части дифференциального уравнения) совпадает с однократным корнем 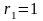характеристического уравнения, то будем искать частное решение в виде:

.

Вычислим производные функции до второго порядка:

.

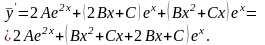
Подставим полученные производные в исходное уравнение:

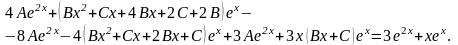
Упростим

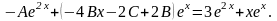
Тог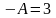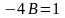да , , . Отсюда

, , .

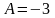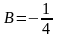И частное решение имеет вид:

.

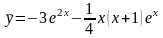Тогда общее решение неоднородного уравнения:

.

Ответ: .

Р я д ы