
- •1. Неопределенный интеграл.
- •2. Формулы интегрирования и таблица основных интегралов.
- •3. Интегрирование методом подстановки или замены переменной.
- •4. Интегрирование по частям.
- •5. Интегрирование рациональных дробей.
- •6. Интегрирование иррациональных выражений.
- •7. Интегрирование тригонометрических функций.
- •8. Определенный интеграл.
- •9. Несобственные интегралы. Интегралы с бесконечными пределами
- •10. Приложения определенного интеграла.
- •11. Двойной интеграл.
- •12. Тройной интеграл.
- •1. Дифференциальные уравнения первого порядка. Уравнения с разделяющимися переменными
- •Линейные уравнения первого порядка
- •Однородные уравнения
- •Определение типа дифференциального уравнения первого порядка
- •Понижение порядка дифференциального уравнения
- •Пример 5. Решить уравнение .
- •Системы дифференциальных уравнений
- •2. Линейные дифференциальные уравнения высшего порядка с постоянными коэффициентами
- •Общее решение однородного линейного дифференциального уравнения с постоянными коэффициентами
- •Общее решение неоднородного линейного дифференциального уравнения с постоянными коэффициентами
- •1. Числовые ряды.
- •Ряды с положительными членами
- •Пусть даны два ряда с положительными членами
- •Ряды с произвольными членами
- •2. Степенные ряды.
- •Ряд Тейлора
- •Разложение основных элементарных функций в ряд Маклорена
- •Интегрирование дифференциальных уравнений с помощью рядов
- •3. Ряд Фурье.
- •1. Вычислить неопределенные интегралы:
- •2. Вычислить несобственные интегралы или доказать их расходимость.
- •3.Вычислить объем тела, полученного вращением кривых и вокруг оси .
- •5. С помощью тройного интеграла вычислить объем тела, ограниченного заданными поверхностями. Сделать рисунки областей и .
- •7. Для данного дифференциального уравнения второго порядка найти частное решение, удовлетворяющее заданным начальным условиям: , , .
- •9. Разложить в ряд Фурье функцию на отрезке .
- •Литература.
10. Приложения определенного интеграла.
1.
Площадь области, ограниченной кривой
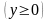 ,
осью
и прямыми
и
равна
,
осью
и прямыми
и
равна
 (17)
(17)
(площадь
участков с должна браться по модулю). При
параметрическом задании функции
должна браться по модулю). При
параметрическом задании функции
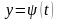 ,
,
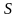 будет равна
будет равна
 . (18)
. (18)
В
полярной системе координат площадь
,
ограниченная кривой
 и двумя лучами
и двумя лучами
 и
и
 равна
равна
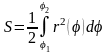 . (19)
. (19)
2.
Длина дуги плоской, дифференцируемой
на отрезке
кривой, заданной уравнением
,
 равна
равна
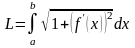 . (20)
. (20)
При
параметрическом задании кривой
,
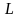 равна
равна
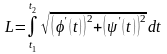 . (21)
. (21)
В
полярной системе координат длина дуги
кривой, заданной уравнением
,
где
 ,
находится по формуле
,
находится по формуле
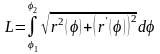 . (22)
. (22)
3. Площадь поверхности, образованной вращением кривой вокруг оси , равна
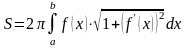 . (23)
. (23)
4. Объем тела, полученного вращением кривой вокруг оси , равен
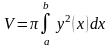 . (24)
. (24)
11. Двойной интеграл.
Интеграл вида
 (32)
(32)
называется
двойным интегралом от функции
 по заданной на плоскости
по заданной на плоскости
 замкнутой
области
замкнутой
области
 .
При этом функция
предполагается непрерывной в области
.
Если
.
При этом функция
предполагается непрерывной в области
.
Если
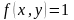 ,
то интеграл
,
то интеграл
 (33)
(33)
в
этом случае имеет смысл площади области
.
Если
 и является определенной функцией
и
,
то интеграл (32) имеет смысл объема тела,
ограниченного сверху поверхностью
и является определенной функцией
и
,
то интеграл (32) имеет смысл объема тела,
ограниченного сверху поверхностью
 ,
снизу плоскостью
,
снизу плоскостью
 ,
а с боков поверхностью цилиндра,
образующие которой параллельны оси
,
а с боков поверхностью цилиндра,
образующие которой параллельны оси
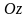 ,
а направляющей является граница области
.
,
а направляющей является граница области
.
Двойной интеграл обладает следующими свойствами:
1.
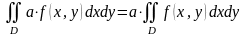 ,
,
 . (34)
. (34)
2.
 . (35)
. (35)
3.
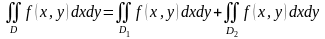 , (36)
, (36)
где
 .
.
Введем для границы области (Рис. 2) следующие обозначения:
дугу
 обозначим как кривую
обозначим как кривую
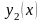
дугу
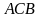 обозначим как кривую
обозначим как кривую

дугу
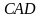 обозначим как кривую
обозначим как кривую
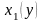
дугу
 обозначим как кривую
обозначим как кривую
 .
.

Вычисление двойного интеграла осуществляется сведением его к двукратному (повторному) интегралу. Используя введенные обозначения можно записать
 . (37)
. (37)
Левый интеграл (по ) в (37) называется внешним интегралом, а правый интеграл (по ) – внутренним. Изменяя порядок интегрирования в двукратном интеграле, можно записать:
 . (38)
. (38)
Для правильной расстановки пределов интегрирования во внутреннем интеграле целесообразно внутри области провести прямую, параллельную оси переменной, по которой осуществляется интегрирование во внутреннем интеграле. Пересечение этой прямой с границами области указывает на значения пределов интегрирования.
Пример
16. Вычислить двойной интеграл
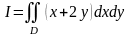 ,
меняя порядок интегрирования по
и
.
Область
ограничена кривыми
,
меняя порядок интегрирования по
и
.
Область
ограничена кривыми
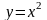 и
и
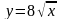 (Рис. 3).
(Рис. 3).

Решение.
Делаем
рисунок области
.
Находим координаты
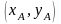 точки
точки
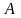 из равенства ординат обеих кривых в
точке
:
из равенства ординат обеих кривых в
точке
:
 ;
;
 ;
;
 .
.
Записываем двойной интеграл в виде двукратного, рассмотрев 2 случая:
а) внутренний интеграл вычисляется по .
Проводим
внутри области
прямую
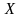 (Рис. 3). Как видно, абсцисса на прямой
изменяется от
(Рис. 3). Как видно, абсцисса на прямой
изменяется от
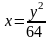 на верхней кривой до
на верхней кривой до
 на нижней кривой. Значения y
во внешнем интеграле изменяются от
на нижней кривой. Значения y
во внешнем интеграле изменяются от
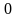 до 16. Т.о. имеем:
до 16. Т.о. имеем:
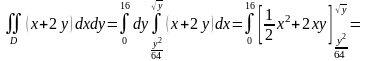

 ;
;
б) внутренний интеграл вычисляется по .
Проводим
внутри области
прямую
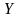 (рис.
3). Ордината на прямой
изменяется
от
на нижней кривой до
(рис.
3). Ордината на прямой
изменяется
от
на нижней кривой до
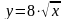 на верхней кривой. Значения
во внешнем интеграле изменяются от
до
на верхней кривой. Значения
во внешнем интеграле изменяются от
до
 .
Т. о. имеем:
.
Т. о. имеем:
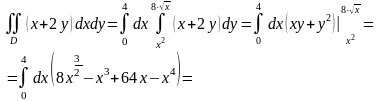
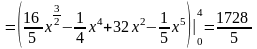 .
.
Результаты вычисления интеграла двумя способами совпадают.
При
вычислении двойного интеграла в полярных
координатах в подынтегральном выражении
делается замена:
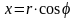 ,
,
 ,
,
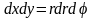 :
:
 , (39)
, (39)
где
 обозначены на рис. 4.
обозначены на рис. 4.

