
- •1. Неопределенный интеграл.
- •2. Формулы интегрирования и таблица основных интегралов.
- •3. Интегрирование методом подстановки или замены переменной.
- •4. Интегрирование по частям.
- •5. Интегрирование рациональных дробей.
- •6. Интегрирование иррациональных выражений.
- •7. Интегрирование тригонометрических функций.
- •8. Определенный интеграл.
- •9. Несобственные интегралы. Интегралы с бесконечными пределами
- •10. Приложения определенного интеграла.
- •11. Двойной интеграл.
- •12. Тройной интеграл.
- •1. Дифференциальные уравнения первого порядка. Уравнения с разделяющимися переменными
- •Линейные уравнения первого порядка
- •Однородные уравнения
- •Определение типа дифференциального уравнения первого порядка
- •Понижение порядка дифференциального уравнения
- •Пример 5. Решить уравнение .
- •Системы дифференциальных уравнений
- •2. Линейные дифференциальные уравнения высшего порядка с постоянными коэффициентами
- •Общее решение однородного линейного дифференциального уравнения с постоянными коэффициентами
- •Общее решение неоднородного линейного дифференциального уравнения с постоянными коэффициентами
- •1. Числовые ряды.
- •Ряды с положительными членами
- •Пусть даны два ряда с положительными членами
- •Ряды с произвольными членами
- •2. Степенные ряды.
- •Ряд Тейлора
- •Разложение основных элементарных функций в ряд Маклорена
- •Интегрирование дифференциальных уравнений с помощью рядов
- •3. Ряд Фурье.
- •1. Вычислить неопределенные интегралы:
- •2. Вычислить несобственные интегралы или доказать их расходимость.
- •3.Вычислить объем тела, полученного вращением кривых и вокруг оси .
- •5. С помощью тройного интеграла вычислить объем тела, ограниченного заданными поверхностями. Сделать рисунки областей и .
- •7. Для данного дифференциального уравнения второго порядка найти частное решение, удовлетворяющее заданным начальным условиям: , , .
- •9. Разложить в ряд Фурье функцию на отрезке .
- •Литература.
1. Неопределенный интеграл.
Пусть
дана функция
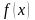 .
Функция
.
Функция
 называется первообразной для
подынтегральной функции
или интегралом от
,
если
является производной для функции
,
т.е.
называется первообразной для
подынтегральной функции
или интегралом от
,
если
является производной для функции
,
т.е.
 и
и
 .
Например, для функции
.
Например, для функции
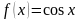 первообразной будет функция
первообразной будет функция
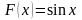 ,
т.к.
,
т.к.
 .
.
Если
является первообразной для
,
то и
 ,
где
,
где
 -
произвольная константа, также будет
являться первообразной для
,
поскольку производная от константы
равна нулю. Совокупность всех первообразных
функций для функции
называется неопределенным интегралом
и обозначается
-
произвольная константа, также будет
являться первообразной для
,
поскольку производная от константы
равна нулю. Совокупность всех первообразных
функций для функции
называется неопределенным интегралом
и обозначается
 .
Таким образом:
.
Таким образом:
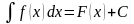 . (1)
. (1)
Из определения неопределенного интеграла вытекают формулы:
 (2)
(2)
 (3)
(3)
Формула (3) может быть использована для проверки правильности интегрирования.
Геометрически
неопределенный интеграл можно
интерпретировать как бесконечное
множество кривых
,
сдвинутых относительно друг друга на
произвольную константу вдоль оси
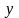 .
.
2. Формулы интегрирования и таблица основных интегралов.
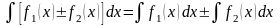
 ,
а – константа.
,
а – константа.
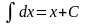 .
.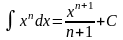 ,
,
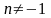 .
.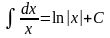 .
. .
. .
. .
.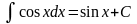 .
.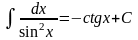 .
.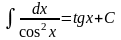 .
.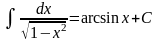 .
.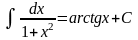 .
.
Вычисление любого сложного интеграла, выражающегося через элементарные функции путем преобразований (если это необходимо), сводится к вычислению интегралов, представленных в таблице. Если интеграл табличный, то интегрирование осуществляется сразу.
Пример 1. Вычислить интеграл
 .
.
Разбиваем интеграл на три интеграла и интегрируем:

Дифференцированием первообразной проверим правильность интегрирования:

Полученное выражение совпадает с подынтегральной функцией, т.е. интегрирование проведено правильно.
3. Интегрирование методом подстановки или замены переменной.
Метод
подстановки заключается в том, что
переходя от переменной
 к
новой переменной
к
новой переменной
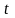 с помощью равенства
с помощью равенства
 или
или
 ,
где
,
где
 и
и
 -
некоторые дифференцируемые (за
исключением, быть может, конечного числа
точек) функции, получаем более простую
подынтегральную функцию, интеграл от
которой вычислить легче, чем от исходной
функции.
-
некоторые дифференцируемые (за
исключением, быть может, конечного числа
точек) функции, получаем более простую
подынтегральную функцию, интеграл от
которой вычислить легче, чем от исходной
функции.
Пример
2. Вычислить интеграл
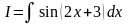 .
Здесь необходимо упростить аргумент
синуса, поэтому делаем подстановку:
.
Здесь необходимо упростить аргумент
синуса, поэтому делаем подстановку:
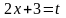 ;
;
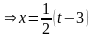 ;
;
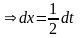 .
.
После подстановки исходный интеграл сводится к табличному:
 .
.
В
этом примере мы использовали подстановку
,
где
 .
.
Пример 3. Вычислить интеграл
 .
.
Делаем подстановку:
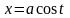 ;
;
 ;
;
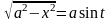 .
.
В
результате интеграл
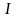 запишется
в виде:
запишется
в виде:
 .
.
В
данном примере использовалась подстановка
,
где
 .
.
4. Интегрирование по частям.
Пусть
две дифференцируемые функции
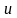 и
и
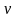 зависят
от
.
Тогда
зависят
от
.
Тогда
 .
.
Интегрируя обе части равенства, получим:

или
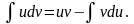 (4)
(4)
Формула (4) называется формулой интегрирования по частям и применяется тогда, когда, например, интеграл в левой части равенства вычислить сложнее, чем интеграл в правой части равенства.
Пример
4. Вычислить интеграл
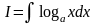 .
Обозначим:
.
Обозначим:
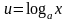 ,
,
 .
Тогда:
.
Тогда:
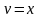 ,
,
 .
По формуле (4) получаем:
.
По формуле (4) получаем:
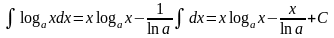 .
.
Пример
5. Вычислить интеграл
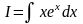 .
Обозначим:
.
Обозначим:
 ,
,
 .
Тогда:
.
Тогда:
 ,
,
 .
По формуле (4) получаем:
.
По формуле (4) получаем:
 .
.
При интегрировании по частям важно правильно выделить функцию в подынтегральной функции.
5. Интегрирование рациональных дробей.
Пусть дан интеграл вида
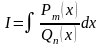 ,
,
где
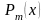 и
и
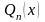 -
полиномы (многочлены) степени
-
полиномы (многочлены) степени
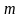 и
и
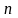 соответственно. Подынтегральная функция
в этом случае будет называться правильной
рациональной дробью, если
соответственно. Подынтегральная функция
в этом случае будет называться правильной
рациональной дробью, если
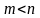 и неправильной рациональной дробью,
если
и неправильной рациональной дробью,
если
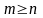 .
Интеграл
в общем случае можно вычислить, если
только
.
Если
,
то необходимо провести деление полинома
на полином
.
В результате получается выражение вида:
.
Интеграл
в общем случае можно вычислить, если
только
.
Если
,
то необходимо провести деление полинома
на полином
.
В результате получается выражение вида:
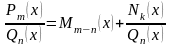 , (5)
, (5)
где
полином
 называется целой частью исходного
выражения, а
называется целой частью исходного
выражения, а
 - остатком от деления. Второе слагаемое
в (5) при этом является правильной дробью,
т.е.
- остатком от деления. Второе слагаемое
в (5) при этом является правильной дробью,
т.е.
 .
.
Пример 6. Представить неправильную дробь
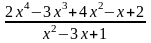
в виде целой части и правильной дроби.
Делаем деление:

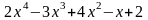
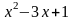


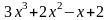
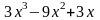



Таким образом:
 .
.
Интегрирование
целой части в (5) не представляет труда.
Для интегрирования правильной дроби,
если
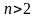 ,
необходимо разложение второго слагаемого
в (5) на более простые дроби. Считая, что
коэффициент при
,
необходимо разложение второго слагаемого
в (5) на более простые дроби. Считая, что
коэффициент при
 в
равен единице (если он не равен единице,
то этого можно добиться очевидным
образом), полином
с вещественными коэффициентами можно,
как доказывается в алгебре, единственным
образом записать в виде:
в
равен единице (если он не равен единице,
то этого можно добиться очевидным
образом), полином
с вещественными коэффициентами можно,
как доказывается в алгебре, единственным
образом записать в виде:
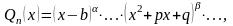 (6)
(6)
где
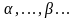 - натуральные числа,
- натуральные числа,
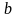 -
вещественные числа, а множители вида
-
вещественные числа, а множители вида
 не имеют вещественных корней (т.е.
дискриминант отрицателен). Тогда второе
слагаемое в (5) можно представить в виде:
не имеют вещественных корней (т.е.
дискриминант отрицателен). Тогда второе
слагаемое в (5) можно представить в виде:
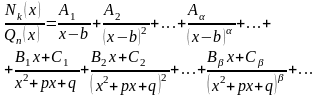 (7)
(7)
где
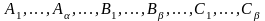 - константы.
- константы.
Как видно из (7), каждому множителю в правой части (6) соответствует столько дробей в правой части (7), какова кратность этого множителя.
Константы
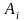 ,
,
 ,
,
 находятся из системы уравнений, которая
получается следующим образом. Все дроби
в правой части равенства (7) приводятся
к общему знаменателю. В числителе правой
части собираются слагаемые с одинаковыми
степенями
и коэффициенты при них приравниваются
к коэффициентам при
в соответствующих степенях в полиноме
.
В результате получается система уравнений
для определения искомых констант.
находятся из системы уравнений, которая
получается следующим образом. Все дроби
в правой части равенства (7) приводятся
к общему знаменателю. В числителе правой
части собираются слагаемые с одинаковыми
степенями
и коэффициенты при них приравниваются
к коэффициентам при
в соответствующих степенях в полиноме
.
В результате получается система уравнений
для определения искомых констант.
Пример 7. Вычислить интеграл

Т.к. степень полинома в числителе больше степени полинома в знаменателе, то разделим числитель на знаменатель, предварительно перемножив сомножители в знаменателе:



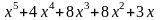



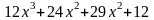
В результате интеграл перепишется в виде:
 .
.
Первый
интеграл легко вычисляется: он равен
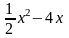 .
Прежде чем вычислять второй интеграл
(обозначим его
.
Прежде чем вычислять второй интеграл
(обозначим его
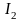 ),
необходимо выяснить, вещественны или
комплексны корни уравнения
),
необходимо выяснить, вещественны или
комплексны корни уравнения
 . (8)
. (8)
От
вида корней зависит вид разложения
подынтегральной функции в
по формуле (7). Т.к. корни уравнения (8)
комплексные (дискриминант
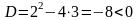 ),
то разложение подынтегральной функции
в
по формуле (7) имеет вид:
),
то разложение подынтегральной функции
в
по формуле (7) имеет вид:

После приведения правой части равенства к общему знаменателю получим:
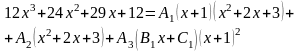
или

Приравнивая коэффициенты при одинаковых степенях в левой и правой части равенства, получим систему уравнений:
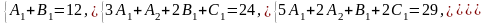
Решая эту систему, найдем:
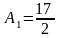 ,
,
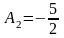 ,
,
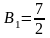 ,
,
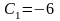 .
.
Таким образом,
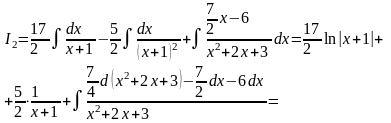
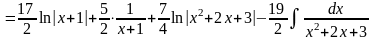 .
.
В последнем интеграле знаменатель приводим к полному квадрату:
 .
.
В результате интеграл дает арктангенс. Окончательно получим:

