2. Оценка облигаций с нулевым купоном

Это самый простой случай. Поскольку денежные поступления по годам за исключением последнего года равны нулю, формула (1) имеет вид:

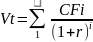
где V_t — стоимость облигации с позиции инвестора (теоретическая стои­мость);

CF — сумма, выплачиваемая при погашении облигации;

n — число лет, через которое произойдет погашение облигации;

FM2(r, n) — дисконтирующий множитель из финансовой таблицы.

Пример

Облигации с нулевым купоном нарицательной стоимостью 100 тыс. руб. и сроком погашения через пять лет продаются за 63012 руб. Проанализировать целесообразность приобретения этих облигаций, если имеется возможность альтернативного ин­вестирования с нормой прибыли 12%.

Анализ можно выполнять несколькими способами; в частно­сти, можно рассчитать теоретическую стоимость облигации и сравнить ее с текущей ценой либо можно исчислить доходность данной облигации. Из формулы 1:

Расчет показывает, что приобретение облигаций является не­выгодным вложением капитала, поскольку доходность данной облигации (8,2%) меньше альтернативной (12%).

3. Оценка бессрочных облигаций

Бессрочная облигация предусматривает неопределенно до­лгую выплату дохода (CF) в установленном размере или по плавающей процентной ставке. В первом случае формула трансформируется в формулу суммы членов бесконечно убыва­ющей геометрической прогрессии, поэтому:

V_t = CF / r

Пример

Исчислить теоретическую стоимость бессрочной облигации, если выплачиваемый по ней годовой доход составляет 10 тыс. руб., а рыночная (приемлемая) норма прибыли — 18%.

По формуле (5.3):

V_t = 10000: 0,18 = 55556 руб.

Таким образом, в условиях равновесного рынка в данный момент времени облигации такого типа будут продаваться по цене 55,6 тыс. руб. По мере изменения рыночной нормы прибыли цена облигации будет меняться.

4. Оценка безотзывных облигаций с постоянным доходом

Денежный поток в этом случае складывается из одинаковых по годам поступлений (С) и нарицательной стоимости облигации (М), выплачиваемой в момент погашения. Таким образом, фор­мула трансформируется в следующую:

(4)

В экономически развитых странах весьма распространенными являются облигационные займы с полугодовой выплатой проце­нтов. Такие займы более привлекательны, поскольку инвестор в этом случае в большей степени защищен от инфляции и, кроме того, имеет возможность получения дополнительного дохода от реинвестирования получаемых процентов.

Преобразовав формулу (4), можно дать общую формулу для расчета внутренней стоимости облигации с выплатой процента каждые полгода:

Пример

Рассчитать рыночную цену облигации нарицательной стоимо­стью 100 тыс. руб., купонной ставкой 15% годовых и сроком погашения через четыре года, если рыночная норма прибыли по финансовым инструментам такого класса равна 10%. Процент по облигации выплачивается дважды в год.

Логика рассуждений в данном случае такова. В условиях равновесного рынка текущая рыночная цена облигации совпада­ет с ее текущей теоретической стоимостью, т.е. Р_m = V_t, и может быть найдена по формуле (5). Денежный поток в данном случае можно представить следующим образом: имеется восемь пери­одов; в каждый из первых семи периодов денежные поступления составляют 7,5 тыс. руб. (100 · 15% : 2 : 100%); в последнем пери­оде помимо 7,5 тыс. руб. инвестору причитается еще нарицатель­ная стоимость облигации. Поскольку рыночная норма прибыли составляет 10%, коэффициент дисконтирования в расчете на по­лугодовой период составит 5%. Дисконтирующий множитель для n = 8 и r = 5% равен 6,463. Таким образом, из формулы (5):

Р_m = V_t = 7,5 · 6,463 + 100 / 1,05⁸ = 116,2 тыс. руб.

Именно по такой цене данные облигации стали бы продавать­ся на рынке ценных бумаг. Легко заметить, что текущая сто­имость облигации в значительной степени зависит от рыночной нормы прибыли (т.е. средней доходности альтернативных ин­вестиций в ценные бумаги такого же класса). Так, если в нашем примере рыночная норма прибыли составляла бы 18%, то теку­щая рыночная цена облигации равнялась бы:

V_t = 7,5 · 5,535 + 100 / 1,09⁸ = 91,7 тыс. руб.

Рассмотренная задача позволяет сделать следующие выводы относительно поведения цены облигации на рынке ценных бумаг:

если рыночная норма прибыли превосходит фиксированную купонную ставку, облигация продается со скидкой (дисконтом), т.е. по цене ниже номинала;

если рыночная норма прибыли меньше фиксированной купон­ной ставки, облигация продается с премией, т.е. по цене выше номинала (разница между рыночной ценой и номиналом носит название «ажио»);

если рыночная норма прибыли совпадает с фиксированной купонной ставкой, облигация продается по нарицательной сто­имости;

рыночная норма прибыли и текущая цена облигации с фик­сированной купонной ставкой находятся в обратно пропорци­ональной зависимости — с ростом (убыванием) рыночной нормы прибыли текущая цена такой облигации убывает (возрастает).