14. Теорема, устанавливающая необходимое и достаточное условие существования базисного решения системы ограничений, безотносительно к способу их получения.

Предикат   является истинным для всех   тогда и только тогда, когда множество истинности предиката   содержится в множестве истинности предиката  , т.е. предикат   является следствием предиката  . При этом предикат   называют необходимым условием для предиката  , а предикат   — достаточным условием для  .

Пример. Рассмотрим утверждение: “Если число   делится на 6, то число   делится на 3”. Здесь предикат  : “Число   делится на 6”, а предикат  : “Число   делится на 3”. Предикат   логически следует из предиката  . Предикат   (делимость числа   на 6) является достаточным условием для предиката   (делимость числа   на 3). Предикат   (делимость числа   на 3) является необходимым условием для предиката   (делимость числа   на 6).

Часто встречается ситуация, при которой истинны теоремы

Это возможно при условии, что предикаты   и   равносильны. В таком случае из первой теоремы следует, что условие   является достаточным для  , а из второй теоремы следует, что условие   является необходимым для  . Таким образом, в этом случае условие   является и необходимым, и достаточным условием для  . Аналогично, условие   является необходимым и достаточным для  .

Пример. Рассмотрим теоремы: “В описанном четырехугольнике суммы длин противоположных сторон равны” и “Если в четырехугольнике суммы длин противоположных сторон равны, в этот четырехугольник можно вписать окружность”. Обе они истинны. Каждое из условий “В четырехугольнике суммы длин противоположных сторон равны” и “В четырехугольник можно вписать окружность” является и необходимым, и достаточным.

15. Геометрический смысл понятия базисного допустимого решения.

Рассмотрим следующую задачу линейного программирования:

,  ,  .

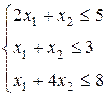Геометрическая интерпретация решения:

  .

Нормальное уравнение прямой:  ,

,

,

.

Рис. 3.1. Геометрическая интерпретация решения экстремальной задачи

То есть наискорейшее возрастание функции F будет в направлении вектора  . Координаты точки В удовлетворяют уравнению:

        .

Можно показать, что если задача линейного программирования имеет решение, то оно соответствует хотя бы одной угловой точке многогранника решений и совпадает, по крайней мере, с одним из допустимых базисных решений системы ограничений. Поэтому для решения задачи линейного программирования необходимо перебрать конечное число базисных решений, выбрать среди них то, на котором целевая функция принимает экстремальное значение. Геометрически это соответствует перебору всех угловых (крайних) точек многогранника. Если оптимальное решение существует, то такой перебор приведет к нахождению оптимального решения. Однако такой прямой перебор связан с очень большим объемом вычислений. Число перебираемых допустимых базисных решений можно сократить, если производить перебор не произвольно, а добиваясь того, чтобы каждое последующее решение было бы не хуже предыдущего. Такой подход, хотя и не исключает теоретической возможности перебора всех угловых точек, на практике позволяет существенно сократить число шагов при отыскании экстремума. Поясним это на графическом примере (см. рис. 3.2).

Пусть область допустимых решений изображается многоугольником ABCDEFGH. Пусть угловая точка B соответствует исходному допустимому базисному решению. При произвольном переборе всех вершин мы могли бы исследовать все семь вершин многогранника. В то же время видно, что после точки Bвыгоднее перейти к точке C , а затем к точке D, которая и будет оптимальной, т.е. вместо семи точек перебрали только три.

Идея последовательного улучшения решения легла в основу наиболее часто применяемого метода решения задач линейного программирования.

 

Рис.3.2. Область допустимых решений

Геометрический смысл симплексного метода состоит в том, что осуществляется последовательный переход от одной вершины многогранника ограничений к другой, соседней, в которой линейная функция принимает значение не худшее, чем в предыдущей. Эта процедура продолжается до тех пор, пока не будет найдено оптимальное решение. Симплексный метод, позволяющий решать любую задачу линейного программирования, универсален. В настоящее время он используется в программном обеспечении для решения задач линейного программирования на компьютере. Для решения задач небольшой размерности он может использоваться вручную.