11. Линейное программирование (лп). Специфика задач лп
Линейное
программирование —
математическая дисциплина, посвящённая
теории и методам решения экстремальных
задач на
множествах 
-мерного векторного
пространства,
задаваемых системами линейных уравнений
и неравенств.Линейное программирование
является частным случаем выпуклого
программирования,
которое в свою очередь является частным
случаем математического
программирования.
Одновременно оно — основа нескольких
методов решения задач целочисленного и нелинейного
программирования.
Одним из обобщений линейного
программирования является программирование.
Многие свойства задач линейного
программирования можно интерпретировать
также как свойства многогранников и
таким образом геометрически формулировать
и доказывать их.
Общей
(стандартной) задачей линейного
программирования называется
задача нахождения минимума линейной
целевой функции (линейной формы) вида
Задача, в которой фигурируют ограничения в форме неравенств, называется основной задачей линейного программирования (ОЗЛП)
,
.
Задача линейного программирования будет иметь канонический вид, если в основной задаче вместо первой системы неравенств имеет место система уравнений с ограничениями в форме равенства[4]:
,
Основную задачу можно свести к канонической путём введения дополнительных переменных.
Задачи линейного программирования наиболее общего вида (задачи со смешанными ограничениями: равенствами и неравенствами, наличием переменных, свободных от ограничений) могут быть приведены к эквивалентным (имеющим то же множество решений) заменами переменных и заменой равенств на пару неравенств.
Легко
заметить, что задачу нахождения максимума
можно заменить задачей нахождения
минимума, взяв коэффициенты 
с
обратным знаком.
13. Фундаментальное понятие базиса. Базисное, базисное допустимое и оптимальное базисное решение задачи лп.
1.Общей задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения функции
(10.10)
при условиях
(10.11)
(10.12)
.
(10.13)
Функция (10.10) называется целевой функцией (или линейной формой) задачи (10.10) – (10.13), а условия (10.11) – (10.13) – ограничениями данной задачи.
2. Стандартной (или симметричной) задачей линейного программирования называется задача, которая состоит в определении максимального для «≤» (минимального для «≥») значения функции (10.10) при выполнении условий (10.11) и (10.13), где k = m, s = n.
3. Канонической (или основной) задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения функции (10.10) при выполнении условий (10.12) и (10.13), где k = 0, s = n.
Каноническая (основная) форма |
Стандартная (симметричная) форма |
Общая форма |
1) ограничения |
||
Уравнения
|
Неравенства
|
Уравнения и неравенств
|
2) условия неотрицательности |
||
Все переменные
|
Все переменные , |
Часть переменных
, |
3) цель задачи
|
||
max F(x) или minF(x) |
max F(x) [min F(x)] |
max F(x) или min F(x) |
.
.
.
, 
, 
.
max F(x) = – min[– F(x)], min F(x) = – max[– F(x)].
Указанные
выше три формы задачи линейного
программирования эквивалентны в том
смысле, что каждая из них может быть
преобразована к форме другой. Совокупность
чисел 
,
удовлетворяющих ограничениям (10.11) –
(10.13), называется допустимым
решением (или планом).
Запишем основную задачу линейного программирования в векторной форме. Найти максимум (минимум) функции
при условиях
,
(10.14)
где 
–
скалярное произведение; 
и 
– m-мерные
вектор-столбцы, составленные из
коэффициентов при неизвестных и свободных
членов системы уравнений задачи.
План Х называется опорным
планом основной
задачи линейного программирования,
если система векторов 
,
входящих в разложение (10.14) с положительными
коэффициентами 
,
линейно независима.
Опорный план называется невырожденным, если он содержит ровно m положительных компонент, в противном случае он является вырожденным.
План 
,
при котором целевая функция принимает
свое максимальное (минимальное) значение,
называется оптимальным.
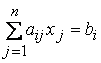
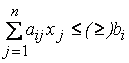