29. Проблема зацикливания алгоритма прямого «симплекс-метода».

Рассмотренный простейший симплекс-метод склонен к зацикливанию и медленно сходится, если длина ребра симплекса   выбрана малой (выбор же большой длины ребра симплекса обеспечивает высокую скорость сходимости, но дает малую точность решения). Поэтому в вычислительной практике используются различные модификации простейшего метода, направленные на преодоление его указанных недостатков.

Основной идей модифицированного симплекс-метода является изменение по некоторому правилу размера симплекса в процессе поиска. При этом наряду с условием (8) в качестве условия окончания итераций можно использовать условие

(9)

где   - текущая длина ребра симплекса,   - требуемая точность решения по  .

Обычно размер симплекса изменяется при выполнении следующих условий:

• при «накрытии» симплексом дна оврага или точки минимума;

• при циклическом движении.

«Накрытие» симплексом дна оврага или точки минимума. Пусть   - вершина, которая получилась на  -ой итерации в результате отражения вершины  . Так что координаты вершин нового симплекса равны      .

Ситуация   интерпретируется как «накрытие» этим симплексом дна оврага или точки минимума и простейший симплекс-метод модифицируется следующим образом (см. рис. 5):

1. Полагаем  = +1 (если  = +2, то полагаем  =1);

2. Выполняем отражение  -ой вершины симплекса  ;

3. Если  ( )> ( ) и не все вершины перебраны, то переходим к п.1.

4. Иначе - продолжаем итерации по схеме простейшего симплекс-метода

  Траектория поиска минимума функции Розенброка модифицированным симплекс-методом при «накрытии» дна оврага. Пунктиром показаны отвергнутые симплексы.

Циклическое движение. Ситуация, когда некоторая вершина симплекса не исключается на протяжении   итераций, интерпретируется как «зацикливание» алгоритма. Простейший симплекс-метод модифицируется в этом случае следующим образом:

1. Находим вершину текущего симплекса  , в которой функция  ( ) принимает наименьшее значение 

2. По формуле (7) выполняем редукцию симплекса   к вершине  .

3. Продолжаем итерации по схеме простейшего симплекс-метода

Здесь количество итераций   рекомендуется находить из условия   где  *  - символ ближайшего целого большего.

30. Вырожденное базисное допустимое решение и вырожденная задача лп.

Если на каком-либо шаге наибольшее возможное значение переменной (оценочное отношение) достигается в нескольких уравнениях одновременно, то разрешающим можно выбрать любое из этих уравнений. На следующем шаге получится вырожденное базисное решение (одна из базисных переменных равна нулю), а переход к очередному базисному решению может не изменить значения целевой функции.

Пусть в примере 1 запас ресурса R₃ равен 4 единицам. Тогда на первом шаге получим одинаковые оценочные отношения в третьем и четвертом уравнениях.

 

Выражая переменную х₁ из четвертого уравнения и подставляя в остальные уравнения, получим:

 

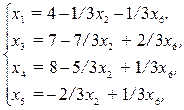
Целевая функция примет вид:  . Новое базисное решение (4, 0, 7, 8, 0, 0). Значение целевой функции 20 >0. Произошло увеличение значения целевой функции, но в выражении для F есть переменная х₂ с положительным коэффициентом. Т.е. ее увеличение могло бы привести к росту значения целевой функции. Однако любое её увеличение, отличное от нулевого, приведет к недопустимому значению переменной х₅. Формально переведем переменную х₂ в базисные переменные (вместо х₅). Выразим её из последнего уравнения и подставим в остальные:

 

Целевая функция примет вид:  . Новое базисное решение (4, 0, 7, 8, 0, 0). При этом значение целевой функции не изменилось и не может быть увеличено, т.к. в выражении целевой функции нет положительных коэффициентов при неосновных переменных.