5. ЗУБЧАТЫЕ ЦИЛИНДРИЧЕСКИЕ ПРЯМОЗУБЫЕ

ПЕРЕДАЧИ

5.1. Краткие сведения из геометрии и кинематики

эвольвентных зацеплений

Геометрию зубчатых передач изучают в курсе «теория механизмов и машин» [6, c.20]. Вспомним лишь то, что необходимо для силовых расчётов и конструирования зубчатых передач, изучаемых дисциплиной «Детали машин».

Термины, определения и обозначения, относящиеся к геометрии и кинематике зубчатых передач с постоянным пере­даточным числом, установлены ГОСТ 16530-83. То же для цилиндрических передач регламентировано ГОСТ 16531-83. Расчет геометрических параметров цилинд­рических зубчатых передач выполняют по ГОСТ 16332-70.

На рис. 5.1 показана схема эвольвентного зубчатого зацепле­ния с обозначением его основных геометрических параметров. Нормаль АВ к эвольвентному профилю рабочих поверхностей зубьев в полюсе зацепления (точка П) называют линией зацепления. Угол зацепления α_w это угол между линией зацепления AВ и прямой, перпендикулярной межосевой линии О₁ О₂.

Начальные окружности (диаметрами d_w1 , d_w2) – это окружности, которые в процессе зацепления колес пере­катываются одна по другой без скольжения. Следует запомнить, что у пары зубчатых колес может быть множество начальных окружностей. У отдельно взятого колеса начальной окружности не существует.

Делительные окружности (диаметром d₁, d₂) – это окружности, на которых шаг и угол зацепления соответ­ственно равны шагу и углу зацепления инструментальной рейки. Делительная окружность принадлежит отдельно взятому колесу. При кор­рекции зубьев колес эта окружность остается неизменной.

Межосевое расстояние передачи а_w (см. рис. 5.1, отрезок о₁О₂) равно полусумме делительных диаметров колес:

а_w = (d₁ + d₂)/2 (5.1)

Рис. 5.1. Геометрия цилиндрической зубчатой передачи

Окружной шаг p_t – расстояние между одноименны­ми точками профилей двух соседних зубьев по дуге делительной ок­ружности.

Модуль т – основная характеристика размеров зубьев. Модули зубчатых колес регламентирует ГОСТ 9563-80. Значение модуля вычисляют по формуле:

m_t = P_t /π (5.2)

Длина делительной окружности зубчатого колеса равна l= π d= p_t z.

Отсюда диаметр делительной окружности колеса с учетом (5.2):

d =m ∙ z (5.3)

Параметры исходного контура цилиндрических зубчатых колес стандартизованы ГОСТ 13755-81:

1) угол профиля α_w =20°;

2) коэффициент высоты головки зуба h_a^*=1;

3) коэффициент радиального зазора c^*=0,25^.m; при обработке зубьев долбяком и шеверами c^*= 0,35; при шлифовании зубьев c^* = 0,4 [7, с.166];

4) коэффициент радиуса закругления у основания зуба ρ_f^* = 0,38.

Диаметры окружностей выступов d_a и окружностей впадин d_f (см. рис. 5.1) равны:

d_a = d + 2h_a , d_f = d – 2h_f , (5.4)

где h_а – высота головки зуба; h_a= h_a^*m;

h_f - высота ножки зуба; h_f =( c^*+ h_a^*)m.

Ширина зубчатого венца колеса: , (5.5)

где ψ_ва – коэффициент ширины зубчатого венца по межосевому расстоянию.

В зависимости от величины этого коэффициента различают зубчатые колёса:

• узкие (ψ_ва =0,2...0,3),

• средние (ψ_ва = 0,315...0,630) и

• ши­рокие (ψ_ва ≥0,63) колеса.

К основным кинематическим параметрам цилиндрической передачи относят:

1) передаточное число

u = z₂ / z₁ = d₂ / d₁, (5.6)

где z_1, z₂ – число зубьев соответственно: шестерни и колеса.

Обычно передаточные числа ограничиваются габаритами переда­чи. В редукторах общего машиностроения максимальные значения пе­редаточных чисел быстроходной ступени U₁ = 6,3…8,0; для промежуточной и тихоходной ступеней u_maх = 5,6…6,3 (нижние значения - при твердости зубьев 56...63НRC, верхние - при твердости не более 350 НВ) [4, с.154];

2) коэффициент торцового перекрытия:

. (5.7)

Здесь знак “ + " для внешнего зацепления; знак " – " для внутреннего зацепления.

Расчет коэффициента перекрытия для пере­дач со смещением приведен в ГОСТ 16532-70. В прямозубых передачах коэффициент ε_α < 2; чаще всего ε_α = 1,2...1,8 [7, c.161];

3) окружная скорость в зацеплении:

(5.8)

где ω – угловая скорость зубчатого колеса, рад/с;

n – частота вращения колеса, об/мин.

5.2. Силы, действующие в зацеплении

При работе зубчатой передачи между зубьями сопряженных колёс возникают силы нормального давления F_n, направленные по линии зацепления. Вместе с тем, в результате относительного скольжения профилей зубьев в зацеплении возникаю­т силы трения F_f = f∙F_n (f – коэффициент трения).

При определении усилий в зацеплении силами трения пренебрега­ют, поскольку величина коэффициента трения в зоне контакта мала. При наличии смазки в зацеплении f = 0,05...0,08 [2, c. I85].

Силу нормального давления на зуб колеса F_n можно разложить на две составляющие:

• окружную F_t , направленную по касательной к окружности, и

• радиальную F_r , направленную по радиусу колеса к его центру.

Окружную и радиальную составляющие силы Fn можно определить по зависимостям:

F_t = F_n ∙ cos α_tw; F_r = F_n ∙ sin α_tw (5.9)

С другой стороны, составляющие силы нормального давления могут быть определены следующим образом:

F_t = T / (0,5 d_tw); F_r = F_t ∙ tg α_w. (5.10)

На работоспособность передачи оказывают влияние контактные напряжения σ_H, возникающие в поверхностном слое рабочей гра­ни зуба (рис. 5.2), и напряжения изгиба σ_F, действующие в по­перечном сечении ножки зуба, т.е. в сечении у его основания (рис. 5.3).

Расчет на усталостную прочность зубьев эвольвентных закрытых передач стальными колесами с модулем не менее 1,00 мм стандартизо­ван ГОСТ 21354-87, который регламентирует структуру расчетных за­висимостей.

При расчете зубьев на контактную прочность принят индекс “H” (по имени автора теории расчета Herz – Герца). При расчете зубьев на усталостную прочность по напряжениям изгиба – индекс “F” (от анг­лийского слова “foot” – нога).

Согласно ГОСТ 21354-87:

а) общие коэффициенты для расчета по контактным напряжениям σ_H и напряжениям изгиба σ_F, обозначены буквой “К”;

б) специфические коэффициенты только для расчета по контактным напряжениям σ_H обозначены буквой “Z”;

в) специфические коэффициенты для расчета по напряжениям изгиба σ_F обозначены буквой “Y”.

5.3. Расчет зубьев на контактную прочность

Расчет выполняют для зацепления в полюсе, т.к. выкраши­вание рабочих поверхностей зубьев начинается у полюсной линии.

В качестве исходной принята формула Герца для определения максимальных контактных напряжений σ_{H max} (см. рис. 5.2), возникающих при сжатии двух цилиндров, соприкасающихся по образующим.

Таким образом, задача контакта двух зубьев эвольвентного профиля сводится к задаче контакта двух цилиндров радиусами ρ₁ и ρ₂:

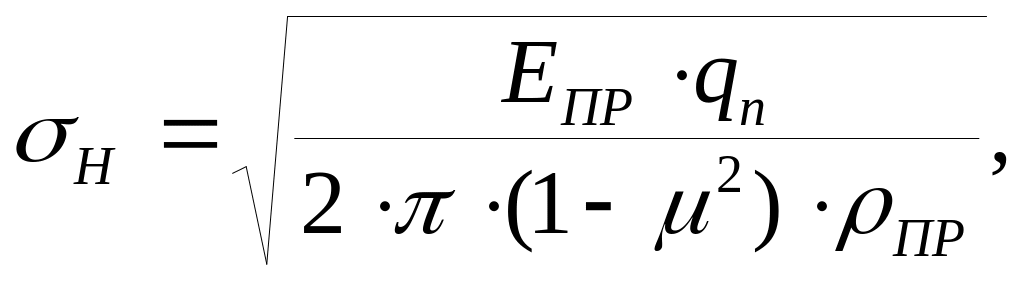(5.11)

где Е_пр – приведенный модуль Юнга материалов парных колес;

Е_пр = 2Е₁ ∙Е₂ /(Е₁ +Е₂ );

q_n – удельная нормальная нагрузка на зуб, т.е. нагрузка, действующая на единицу длины зуба (см. рис. 5.3);

ρ_пр – приведенный радиус кривизны профилей зубьев, зацепляющихся в полюсе п (см. рис. 5.2);

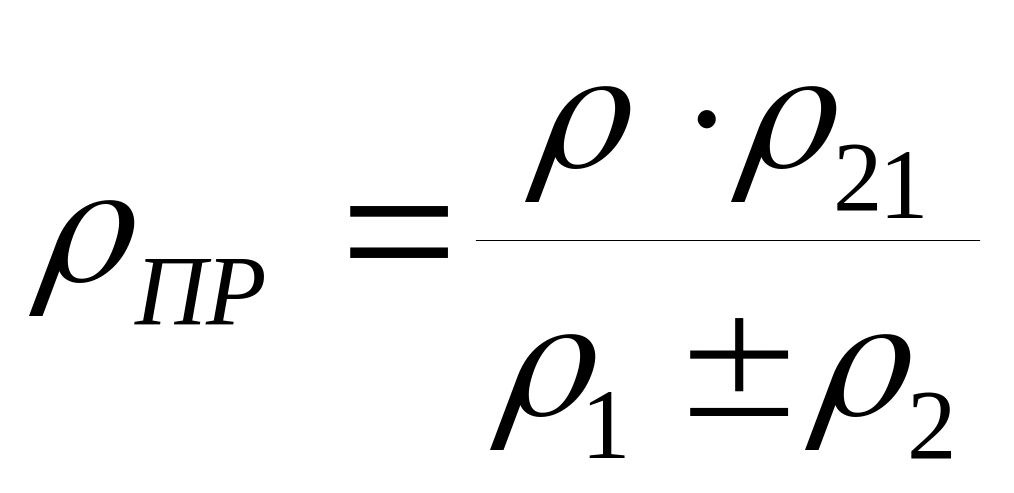(5.12)

В ф. (5.12) знак “+” принимают для внешнего зацепления колес, а знак “– “ используют для внутреннего зацепления.

Рис. 5.2. – К расчету эвольвентного зацепления

на контактную прочность зубьев

Расчетная удельная нормальная нагрузка на зуб, выраженная через окружную силу в зацеплении F_{t ,} может быть определена по зависимости:

(5.13)

где K_Hα – коэффициент, учитывающий неравномерность распределе­ния на грузки между зубьями; для прямозубых колес K_Hα =1,0;

K_Hβ – коэффициент неравномерности распределения нагрузки по длине контактных линий зубьев; выбирают по соответствующим таблицам в за­висимости от твердости зубьев и ширины колеса [3, c.I39];

K_HV – коэффициент динамической нагрузки, возникающей в за­цеплении [3, c. 138];

b_w – рабочая ширина зубчатого венца колеса (или длина зуба);

b_w =ψ_вa ∙ a_w .

Из рис. 5.2 видно, что: ρ₁=0,5d_w1 ∙sin d_w; ρ₂=0,5d_w2 ∙sin d_w (5.14)

Вместе с тем, начальные диаметры колеса и шестерни связаны между собой зависимостью d_w2 = d_w1 ∙u.

Тогда, учитывая (5.12) и (5.14), получим:

(5.15)

Подставив значения q_n и ρ_пр в (5.11) и выполнив некоторые преобразования, получим:

(5.16)

где Z_н – коэффициенты формы сопряженных поверхностей зубьев в полюсе зацепления; . При α_w=20⁰ Z_H=2,5;

Z_Е – коэффициент, учитывающий механические свойства материалов сопряженных колес; ; для стальных колес Z_Е =190 Н^1/2 /мм;

Z_ε – коэффициент, учитывающий суммарную длину контактных линий сопряженных зубьев; ; для прямозубых колёс (при ε_σ =1,6) коэффициент Z_ε = 0,9.

Если подставить в формулу (5.16):

b_w =ψ_ва ∙а_w , F_t = T₂ /(0,5d_w2) d_w2 = d_w1 ∙u=2a_w ∙u /(u±1), то получим условие обеспечения контактной прочности зубьев колёс:

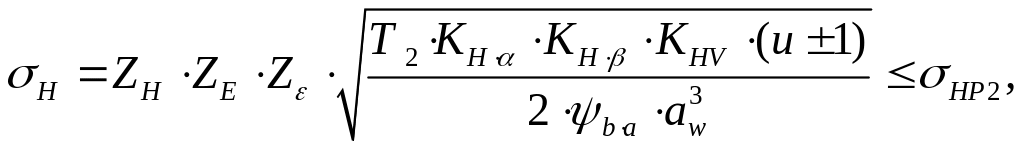(5.17)

где Т₂ – в Н∙мм; σ_н, σ_нР2 – в МПа; а_w – в мм.

Современные технологии изготовления зубчатых передач требуют, чтобы запас прочности по контактным напряжениям не превышал 15%, а перегрузка – не более 5% [3, с.159]. Если результаты проверочного расчета передачи по контактным напряжениям подтвердят эти ограничения, то параметры передачи считают окончательными. Иначе – необходим перерасчет геометрических параметров передачи.

Если перегрузка зубьев превысит 5%, то можно принять меры:

• увеличить ширину зубчатого венца: перейти к следующему стандартному значению коэффициента ширины ψ _ba;

• увеличить межосевое расстояние: перейти к следующему стандартному значению, включая и второй ряд значений а_w;

• назначить другие, более прочные материалы и термообработку для изготовления шестерни и колеса.

Меры перечислены в порядке их усиления.

Из (5.17) может быть получена зависимость для проектного расчета цилиндрической прямозубой передачи:

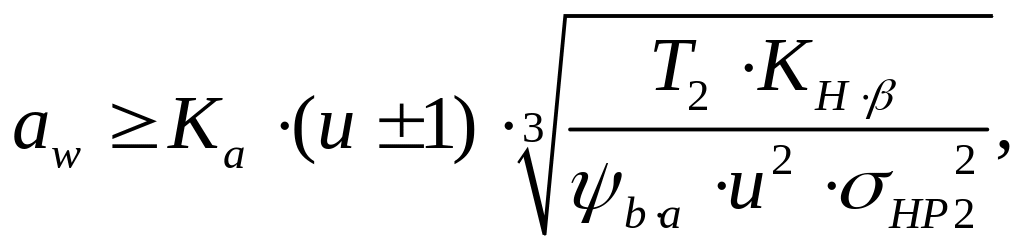(5.18)

где К_а – коэффициент межосевого расстояния; для прямозубых передач

К_а = 49,5(Н/мм²)³; для косозубых и шевронных передач: К_а = 43(Н/мм²)³; расчетная формула: .

Рассчитанное по (5.18) межосевое расстояние должно быть сог­ласовано со стандартным значением по ГОСТ 2185-66.

Входящее в формулы (5.17) и (5.18) параметр σ_нР2 – допускаемые контактные напряжения материала того из зацепляющихся зубчатых колес, для которого принят материал меньшей прочности. Как правило, менее прочными выполняют зубья колеса, т.к. они реже попадают в зацепление, чем зубья шестерни. Величину допускаемых контактных напряжений определяют по зависимости:

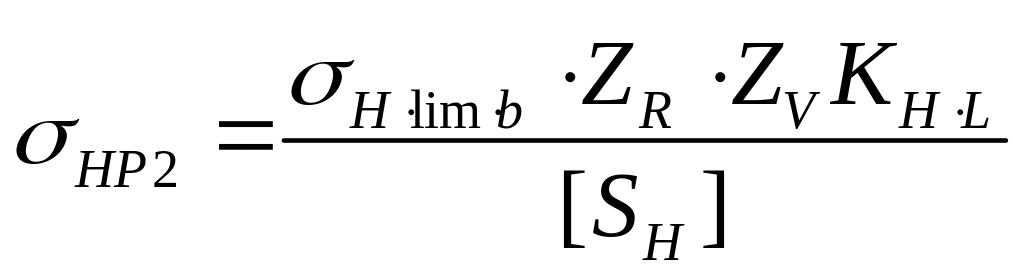(5.19)

где σ_{H lim в} – предел контактной усталости поверхностей зубьев, соответствующий базовому числу циклов напряжений; его рассчитывают по эмпирическим зависимостям в функции поверхностной твердости материалов колес [4, 185] или [2, с.193];

[S_H] – коэффициент безопасности; при однородной структуре материал колеса [S_H]=1, при поверхностном уп­рочнении зубьев колес [S_H] =1,2 [4 с. 185];

Z_R – коэффициент, учитывающий шероховатость сопряженных поверхностей зубьев; при R_a=1,25…0,63 мкм Z_R=1,0;

при R_a = 2,50…1,25мкм Z_R = 0,95;при R_a =10,5…2,5 мкм Z_R =0,9 [4,c.185];

Z_V – коэффициент, учитывающий влияние скорости в зацеплении; при НВ≤350: Z_V = 0,85∙v^0,1; при НВ >350: Z_V = 0,929∙v^0,03; в расчетах нормальной точности принимают: Z_V = 1,00…1,15 [4.c.185];

K_Hl – коэффициент долговечности; ; (базовое число циклов N_o=10⁶ и N – фактическое число циклов нагружения зубьев колес за весь срок службы передачи); при постоянной нагрузке K_Hl=1,0.