Линейное неоднородное дифференциальное уравнение второго порядка с произвольными коэффициентами. Метод Лагранжа.
Рассмотрим метод нахождения частного решения линейного неоднородного дифференциального уравнения второго порядка с произвольными коэффициентами (постоянными или переменными) и правой частью любого вида. Это универсальный метод, его называют методом вариации произвольных постоянных, или методом Лагранжа.
Рассмотрим
этот метод применительно к уравнению
(22). Согласно этому методу сначала находят
два линейно независимых решения
и
соответствующего однородного
дифференциального уравнения. Частное
решение неоднородного дифференциального
уравнения ищется в виде их линейной
комбинации, в которой произвольные
постоянные
и
заменяются на неизвестные функции
и
:
.
(26)
Подстановка этого выражения в неоднородное дифференциальное уравнение (22) приводит к следующему уравнению:
.
(27)
Перегруппируем слагаемые в (27):
(28)
Рассмотрим
подробнее уравнение (28). Так как функции
и
являются решениями однородного
дифференциального уравнения (17), выражения
в третьей и четвертой скобках в (28)
тождественно равны нулю. Наложим на
пока неопределенные функции
и
следующее условие:
(29)
Тогда выражение в пятой скобке в (28) также окажется равным нулю. Продифференцируем обе части равенства (28):
Это соотношение показывает, что и выражение в первой скобке в (28) тождественно равно нулю.
Таким
образом, при условии (29) уравнение (28)
сводится к следующему:
Иными словами, уравнение (28) равносильно
системе уравнений:
(30)
Поскольку определитель этой системы является вронскианом двух линейно независимых решений и , и отличен от нуля, то система всегда имеет единственное решение.
Решив
систему уравнения (30), остается лишь
найти
и
,
то есть проинтегрировать полученные
из (30) функции
,
и
подставить их в выражение для
.
Пример 14. Найти решение дифференциального уравнения:
.
Решение: Это уравнение с постоянными коэффициентами, но его правая часть не имеет специального вида, допускающего применение метода неопределенных коэффициентов.
Поэтому для нахождения частного решения этого линейного неоднородного дифференциального уравнения воспользуемся методом вариации произвольных постоянных. Сначала найдем решение соответствующего однородного дифференциального уравнения:
.
Характеристическое
уравнение
имеет корни
,
и общее решение записывается в виде:
.
Частное решение исходного неоднородного уравнения ищем в виде:
.
Система (30) приобретает вид:
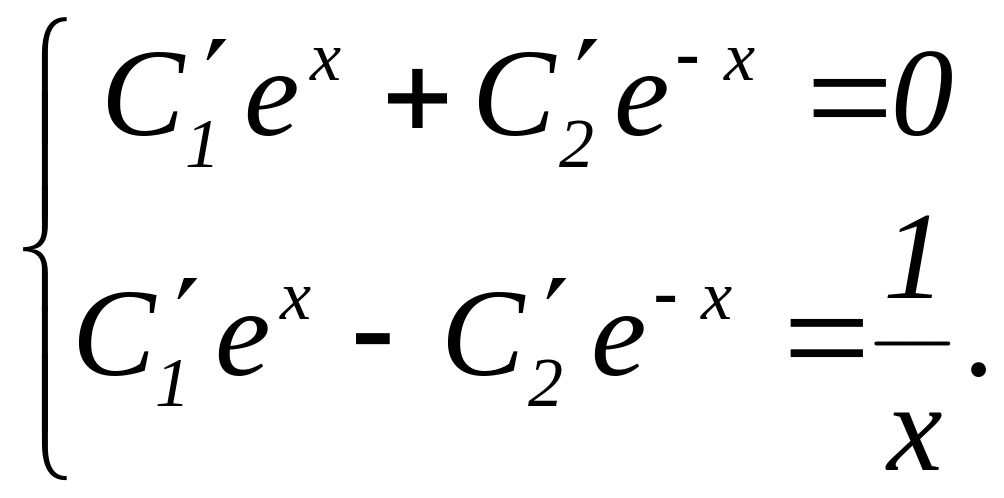
Отсюда находим:
и
В
итоге получаем:
.
Общее решение рассматриваемого уравнения принимает вид:
.
Задача 11.
11.1 – 11.20.
а) Исследовать сходимость ряда.
б) Определить область сходимости ряда.
11.1
а)
,
б)
.
11.2
а)
,
б)
.
11.3
а)
,
б)
.
11.4.
а)
,
б)
.
11.5
а)
,
б)
.
11.6
а)
,
б)
.
11.7
а)
,
б)
.
11.8
а)
,
б)
.
11.9
а)
,
б)
.
11.10
а)
,
б)
.
11.11
а)
,
б)
.
11.12
а)
,
б)
.
11.13
а)
,
б)
.
11.14.
а)
,
б)
.
11.15
а)
,
б)
11.16.
а)
,
б)
.
11.17
а)
,
б)
.
11.18
а)
,
б)
.
11.19.
а)
,
б)
.
11.20
а)
,
б)
