1.Уравнение с разделяющимися переменными.

Дифференциальным уравнением с разделяющимися переменными называется уравнение вида:

Для его решения следует сначала разделить переменные, то есть разнести их в разные стороны уравнения:

( ),

а затем проинтегрировать обе части уравнения:

.

Следует иметь в виду, что полученные неопределенные интегралы могут различаться на произвольную постоянную .

Пример 1. Решить задачу Коши: , .

Решение: Поделим обе части уравнения на Тогда:

и .

Вычисляя интегралы, находим: . Отсюда получаем общее решение:

.

Так как, по условию, >0, то выбираем знак «+»:

.

Подставим в это решение начальное условие:

;

Следовательно, и – искомое частное решение, то есть решение задачи Коши.

2. Однородное уравнение первого порядка.

Однородным уравнением первого порядка называется уравнение вида:

. (6)

Для его решения введем новую переменную . Тогда и . Подставляя эти соотношения в (6), получаем: или . Это уравнение с разделяющимися переменными, и оно легко интегрируется. Найдя , получаем искомое решение .

Пример 2. Решить уравнение: .

Решение: Полагая и , получим:

, или .

Интегрируя обе части последнего уравнения, получим:

.

Для удобства, произвольная постоянная здесь представлена в виде , где . Тогда и окончательно общее решение принимает вид:

.

Пример 3. Решить уравнение: .

Решение: Пусть . Разделим обе части уравнения на :

.

После замены переменной это уравнение приводится к виду:

, или .

Вычислим интеграл в левой части последнего уравнения:

Тогда .

Заметим, что общее решение уравнения можно записать в виде функции, заданной неявно (подставим вместо z):

.

3. Линейное уравнение первого порядка.

Линейное уравнение первого порядка имеет вид:

Решить линейное дифференциальное уравнение первого порядка можно с помощью введения двух новых искомых функций и , положив , и дополнительного условия на одну из них, выби­раемую произвольно. Рассмотрим применение этого метода на следующем примере.

Пример 4. Решить дифференциальное уравнение

.

Решение: Будем искать решение в виде: ;

Тогда ; Подставляя выражения для искомой функции и ее производной в рассматриваемое дифференциальное уравнение, получим:

, или

. (7)

Поскольку одну из функций или мы вправе выбрать произвольно, выберем ее так, чтобы выполнялось условие: Тогда уравнение (7) запишется в виде: . Это уравнение легко интегрируется: ; .

Произвольную постоянную здесь можно положить равной нулю, так как мы выбираем частное решение. Тогда .

После подстановки в исходное уравнение получим (при ):

; ; .

Таким образом, искомое общее решение.

4. Уравнение Бернулли.

Уравнением Бернулли называется уравнение следующего вида:

. (8)

Это уравнение отличается от линейного уравнения множителем в правой части. Здесь и , так как в этих случаях уравнение (8) превращается в линейное уравнение.

Уравнение Бернулли, как и линейное уравнение, решается с помощью представления этой функции в виде .

Пример 5. Решить уравнение:

. (9)

Решение: Это уравнение Бернулли и . Положим . Тогда уравнение (9) запишется в виде:

. (10)

Будем искать функцию как решение уравнения:

.

Тогда и . Вычисляя интегралы, получим:

;

Подставляя полученное выражение в (10), получим:

.

Разделяя переменные и интегрируя, получим:

.

Выполняя интегрирование, приходим к выражению:

, или .

Окончательно получаем: .

Дифференциальные уравнения второго порядка.

Дифференциальное уравнение второго порядка имеет вид:

. (11)

Если уравнение (11) может быть разрешено относительно второй производной, то оно записывается в виде:

.

Задача Коши для дифференциального уравнения второго порядка состоит в нахождении частного решения, удовлетворяющего начальным условиям:

Рассмотрим основные виды дифференциальных уравнений второго порядка.

1. Дифференциальные уравнения, допускающие понижение порядка.

Некоторые дифференциальные уравнения с помощью замены переменных приводятся к уравнениям меньшего порядка, то есть допускают понижение порядка, что упрощает их решение. Применительно к уравнениям второго порядка это позволяет свести задачу к решению дифференциальных уравнений первого порядка.

Рассмотрим основные типы таких уравнений, имея в виду, что применяемые методы пригодны и для уравнений более высокого порядка.

а) Простейшее дифференциальное уравнение второго порядка.

Уравнение такого типа имеет вид:

(12)

Поскольку правая часть уравнения (12) не зависит от и , общее решение может быть найдено непосредственным интегрированием левой и правой частей уравнения. После первого интегрирования получаем:

.

Повторное интегрирование приводит к общему решению:

, (13)

где и постоянные интегрирования.

Пример 6. Найти решение дифференциального уравнения

.

Решение: После первого интегрирования уравнения получим:

После повторного интегрирования имеем:

б) Дифференциальное уравнение, не содержащее искомой функции.

Уравнение такого типа имеет вид:

. (14)

Введем новую функцию Тогда . С учетом этих соотношений уравнение (14) перепишется в виде:

.

Получено уравнение первого порядка. Его решение ищется с помощью методов, изложенных выше. Пусть решение этого уравнения. Поскольку , приходим к уравнению , которое легко интегрируется.

Пример 7. Решить задачу Коши:

,

Решение: Положим Так как , дифференциальное уравнение принимает вид:

.

Это уравнение с разделяющимися переменными. Проинтегрируем его.

, .

Вычисляя интеграл в левой части последнего уравнения, получаем:

, .

Из последнего уравнения находим . Возвращаясь к переменной , получаем:

.

Определим постоянную интегрирования , используя одно из условий задачи Коши: Получаем:

, то есть .

Тогда уравнение для искомой функции приобретает вид:

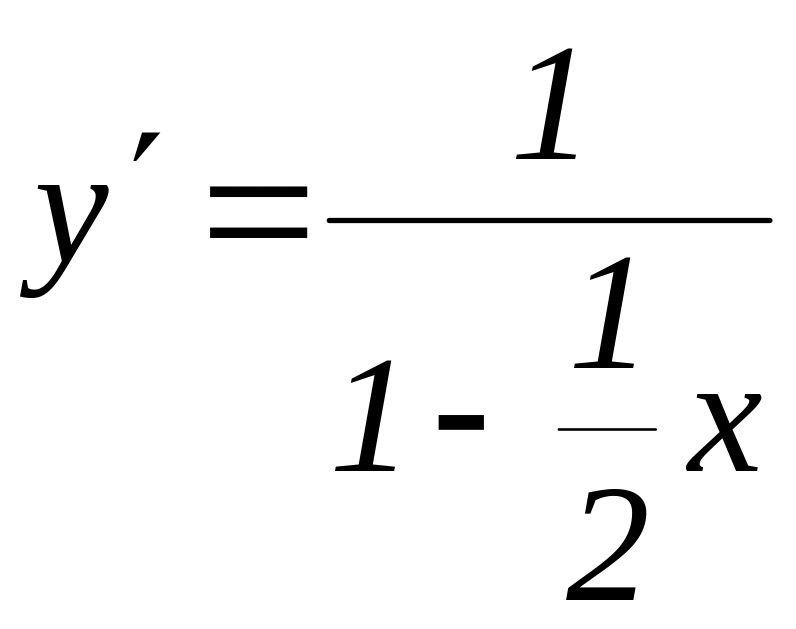или .

Последнее уравнение с разделяющимися переменными легко интегрируется:

.

Найдем значение постоянной интегрирования , используя первое из условий задачи Коши. Получаем: , то есть .

Теперь можно выписать решение задачи Коши:

.

в) Дифференциальное уравнение, не содержащее независимой переменной.

Уравнение такого типа выглядит следующим образом:

. (15)

Вместо функции введем в рассмотрение новую функцию Тогда по правилу дифференцирования сложной функции получаем:

Подстановка этих соотношений в уравнение (15) превращает его в уравнении первого порядка относительно неизвестной функции:

(16)

Пусть общее решение этого уравнения, найденное одним из методов решения дифференциальных уравнений первого порядка. Поскольку , последнее соотношение принимает вид . Мы получили уравнение первого порядка с разделяющимися переменными, которое легко интегрируется.

Пример 8. Найти общее решение дифференциального уравнения .

Решение: Положим Тогда Подставим эти выражения в исходное уравнение: .

После разделения переменных получаем:

, ,

Из последнего уравнения находим: и .

Так как , получаем: , .

Отсюда и

Мы получили общий интеграл исходного дифференциального уравнения в неявном виде:

2. Линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами.

Дифференциальные уравнения этого типа имеет вид:

, (17)

где – постоянные числа.

Будем искать решение уравнения (17) в виде , где постоянное число. После подстановки этого выражения в (17) получим:

.

Поскольку , должно выполняться квадратное уравнение:

. (18)

Это уравнение называется характеристическим уравнением для уравнения (17). В зависимости от величины его дискриминанта возможны три случая:

а) .

Можно показать, что общим решением в этом случае является комбинация двух линейно независимых решений, отвечающих двум различным корням характеристического уравнения:

. (19)

б) .

В этом случае общим решением будет:

. (20)

в) . В этом случае характеристическое уравнение имеет два комплексно-сопряженных корня: и

Общее решение записывается в следующем виде:

. (21)

В формулах (19) – (21) и произвольные постоянные.

Пример 9. Решить дифференциальное уравнение:

;

Решение: Характеристическое уравнение принимает вид:

;

Дискриминант положителен, уравнение имеет два различных корня: . Тогда, согласно (19), общее решение дифференциального уравнения записывается в виде:

.

Пример 10. Решить дифференциальное уравнение: ;

Решение: Характеристическое уравнение имеет один кратный корень . В соответствии с (20) общее решение дифференциального уравнения записывается в виде:

.

Пример 11. Решить дифференциальное уравнение:

.

Решение: Дискриминант характеристического уравнения отрицателен, характеристическое уравнение имеет комплексные корни: В этом случае формула (21) дает следующее общее решение дифференциального уравнения:

.