5. Интегрирование рациональных дробей.

Рациональной дробью называется функция, равная отношению двух многочленов:

,

где m, n – целые положительные числа, – действительные числа ( ).

Если , то называется правильной рациональной дробью, если – неправильной дробью.

Всякую неправильную дробь путем деления на можно представить в виде суммы некоторого многочлена и правильной дроби.

,

где , - многочлены; – правильная рациональная дробь .

Интегрирование правильной рациональной дроби основано на следующей теории.

Каждая правильная рациональная дробь может быть представлена в виде суммы конечного числа простейших дробей следующих четырех видов:

где A, a, M, N, p, q – действительные числа, k – натуральное число .

В алгебре устанавливается, что если знаменатель дроби представить в виде:

то в разложении самой дроби:

а) каждому множителю вида соответствует одна простейшая дробь вида ;

б) каждому множителю вида соответствует сумма простейших дробей вида: ;

в) каждому множителю соответствует одна простейшая дробь вида .

Пример 12. Найти интеграл .

Решение: Разложим правильную рациональную дробь на сумму простейших дробей:

.

Приводя дроби к общему знаменателю и приравнивая числители, получим:

Так как данное тождество должно выполняться для любого , то зададим аргументу значение и получим .

Сравнивая коэффициенты при одинаковых степенях в тождестве, находим:

при :

при :

при :

при :

Подставив значение , находим: , , .

Поэтому получаем:

6. Интегрирование тригонометрических функций.

Рассмотрим интеграл типа , где R обозначает рациональную функцию своих аргументов и . Интеграл данного типа сводится к интегралу от рациональной функции с помощью так называемой универсальной постановки:

.

Действительно, и

= .

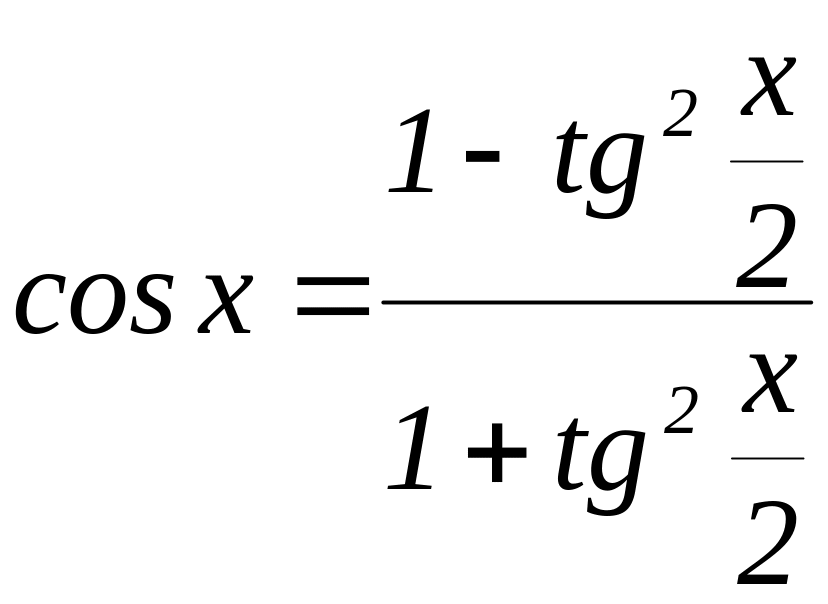Тогда, подставляя в данный интеграл вместо , и полученные выражения, будем иметь под знаком интеграла рациональную функцию.

Пример 13. Вычислить интеграл .

Решение: Подстановка дает:

= =

Универсальная подстановка нередко приводит к сложным вычислениям. Поэтому в указанных ниже случаях предпочтительней частные подстановки, также рационализирующие интеграл.

Если , то применима подстановка ;

если , то применима подстановка ;

если , то применима подстановка .

Пример 14. Вычислить интеграл .

Решение: Положим и найдем:

поэтому:

= = = .

Рассмотрим интеграл вида , где m и n – целые числа. Возможны следующие случаи:

1. Одно из чисел m или n – нечетное, например , тогда полагая , получим:

= = .

2. Оба числа m и n – четные. Тогда рекомендуется воспользоваться тригонометрическими формулами понижения степени:

.

Пример 15. Вычислить интеграл .

Решение:

= = .

7. Интегрирование некоторых иррациональных функций.

Рассмотрим интеграл следующего вида:

,

где R – рациональная функция, – рациональные числа. Данный интеграл сводится к интегралу от рациональной функции с помощью подстановки , где k – общий знаменатель всех дробных показателей.

Пример 16. Вычислить интеграл .

Решение: Положив , получим: = = = .

Задача 9.

9.1 – 9.20. Вычислить площадь фигуры, ограниченной линиями.

9.1. ; .

9.2. ; .

9.3. ; ; .

9.4. ; ; ; .

9.5. ; ; .

9.6. ; .

9.7. ; .

9.8.

9.9.

9.10.

9.11. ; .

9.12. ; .

9.13. ; .

9.14.

9.15. .

9.16. ; .

9.17. ; , .

9.18. ; , .

6.19.

6.20.

Указания к задаче 6: определенный интеграл.

Пусть функция определена на отрезке . Разобьем этот промежуток произвольным образом на n частей точками:

.

В каждом из полученных частичных промежутков , где , выберем произвольную точку . Вычислим значение функции и умножим его на разность , после этого составим сумму , которая называется интегральной суммой Римана для функции на отрезке .

Пусть , т.е. длина наибольшего частичного промежутка. Если существует конечный предел интегральной суммы при , не зависящий ни от способа разбиения промежутка на части, ни от выбора точек , то этот предел называется определенным интегралом функции на промежутке и обозначается символом . Таким образом, .

Функция в этом случае называется интегрируемой в промежутке . Числа и называются соответственно нижним и верхним пределами интеграла.

Выясним геометрический смысл суммы Римана , когда функция непрерывна и неотрицательна в промежутке , . В этом случае произведение равно площади прямоугольника с основанием и высотой , а сумма равна сумме площадей прямоугольников с основанием и высотами (рис. 1).

Рис.1

Таким образом, равна площади ступенчатой фигуры, а определенный интеграл равен пределу при , т.е. площади криволинейной трапеции, ограниченной графиком функции , прямыми и и отрезком оси .