Розв’язання
Рівняння гармонічного коливання має вигляд x=Asin(ωt+φ) (1).
Формулу швидкості одержимо, взявши першу похідну за часом від зміщення X : v=dx/dt=Aωcos(ωt+φ) (2).
Щоб визначити швидкість через зміщення, треба виключити з формул (1), (2) час. Для цього зведемо обидва рівняння в квадрат і розділимо перше на А2, а друге на А2ω2 й складемо їх:
x2 / А2+v2 /А2ω2=1
Розв’язуючи останнє рівняння відносно v, знайдемо: v=±8.2см/с.
Знак + відповідає випадку, коли напрям швидкості збігається з позитивним напрямом осі X.
Силу, що діє на точку, знайдемо за другим законом Ньютона: F = ma(5)
a=dv/dt=-Aω2sin(ωt+φ)
Підставивши цей вираз для прискорення у формулу (5) матимемо:
F =-4π2v2mAsin(ωt+φ)
Звідси отримаємо максимальне значення сили: Fmax=4π2v2mA
Підставивши числові значення величин, знайдемо : Fmax=1.49*10-3H
Повна енергія точки, що коливається, є сумою кінетичної і потенціальної енергій, обчислених для будь-якого моменту часу.
Простіше обчислити повну енергію в мить, коли кінетична енергія досягає максимального значення. У цей момент потенціальна енергія дорівнює нулю. Тому повна енергія Е точки, що коливається, дорівнює максимальній кінетичній енергії і Екmax може бути визначена за формулою: E=mv2/2 (6)
Підставивши цей вираз для швидкості у формулу (6), знайдемо: E=2π2mv2А2
Після підстановки числових значень отримаємо: E=2.21*10-5Дж.
1.4.Явище резонансу під час вимушених механічних коливань
У реальних коливальних системах за рахунок зміни енергії коливального руху виконується робота проти сил тертя й опору. Тому з часом амплітуда вільних коливань зменшується (рис.5.1.5). Коли ж запас енергії вичерпується, коливання припиняються. Коливання, амплітуда яких з часом зменшується, називають загасальними. Інколи цей процес посилюють за допомогою спеціальних пристроїв. Наприклад, у транспортних засобах використовують різні амортизатори, які гасять коливання кузова, зумовлені нерівностями дороги.
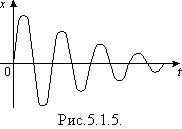
Для того, щоб коливання в системі не загасали, необхідно компенсувати втрати енергії, спричинені дією сили тертя і опору. Енергію в системі треба поповнювати періодично. Це досягається періодичною дією на систему зовнішньої сили. Наприклад, коливання тягарця, підвішеного на пружині, можна підтримувати як завгодно довго, якщо підштовхувати тягарець через рівні проміжки часу.
Коливання системи, які виникають під дією зовнішньої періодично змінної сили, називаються вимушеними.
Зі зміною частоти ν зовнішньої сили змінюються амплітуди вимушених коливань. Якщо ця частота наближається до частоти вільних коливань системи ν 0, то амплітуда вимушених коливань збільшується, досягаючи максимуму, якщо ν = ν0. Зі збільшенням частоти (ν > ν0) амплітуда вимушених коливань зменшується. Явище різкого зростання амплітуди вимушених коливань у разі наближення частоти дії зовнішньої періодичної сили до частоти вільних коливань системи називають резонансом. Графік залежності амплітуди коливань від частоти під час резонансу зображено на рис.5.1.6. Резонансна крива тим гостріша, чим менші втрати енергії в системі.
Приклад перших проявів руйнівної дії резонансу: руйнування підвісних мостів через річку Луару у Франції наприкінці XIX ст. та в Росії на початку ХХ ст. через річку Фонтанка. У першому випадку солдати крокували по мосту в ногу, у другому — гарцювали кінні гренадери. Для послаблення шкідливої дії резонансу в техніці використовують гасителі коливань (демпфери), гумові та повстяні прокладки. Але резонанс може бути не тільки шкідливим. Приклади корисних проявів резонансу: підсилення звуку музичними інструментами (корпус гітари, міхи баяна), настроювання радіоприймача на частоту потрібної радіостанції.
Явище резонансу може бути корисним, оскільки воно дає змогу навіть за допомогою малої сили суттєво збільшити амплітуду, наприклад, укладання бетону за допомогою вібраторів.
Резонанс може бути шкідливим і небезпечним. З метою запобігання цьому слід заздалегідь обчислювати частоти коливань різних машин, засобів транспорту, фундаментів тощо, щоб у звичайних умовах їх експлуатації не міг настати резонанс.
У повсякденному житті можна спостерігати, як в кімнаті бряжчать шибки під час проходження по вулиці важкого вантажного автомобіля. Це означає, що власні частоти коливань шибок дорівнюють частоті коливань деталей автомобіля.