1.3.Математичний і пружинний маятники. Період коливань математичного і пружинного маятників.

Математичний і пружинний маятники є коливальними системами, які за певних умов здійснюють гармонічні механічні коливання.

Математичним маятником називають матеріальну точку, підвішену на невагомій і нерозтяжній нитці. Це ідеальна коливальна система. Якщо подібний маятник не можна вважати матеріальною точкою або не можна знехтувати вагою тіла і розтягом підвісу, то маятник називають фізичним. Такий маятник коливається подібно до математичного.

Підвісимо матеріальну точку масою m на нитці довжиною l і відхилимо отриманий маятник на кут a від положення рівноваги (рис.5.1.3).

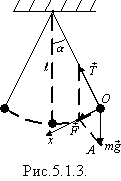
На тіло діятимуть (якщо знехтувати силами тертя і опору повітря) сила тяжіння і сила натягу нитки , рівнодійна яких і буде надавати матеріальній точці прискорення. Це прискорення буде напрямлене в бік положення рівноваги. Модуль рівнодійної цих сил (вертикальної сили) знаходимо із прямокутного трикутника FOA:

F = mgsina.

У разі малих кутів відхилення sin α   α = x/l. Ураховуючи, що напрям зміщення і вертальної сили протилежні, отримаємо , де х - абсолютне значення зміщення маятника від положення рівноваги. Оскільки за другим законом Ньютона F = ma, то прискорення маятника          

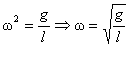
Період коливань математичного маятника

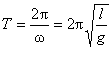(3)

Згідно з формулою (3) можна зробити висновок, що період коливань математичного маятника не залежить від маси тіла, а визначається лише довжиною підвісу і прискоренням вільного падіння.

Ще одним прикладом гармонічного коливання є коливання тіла на пружині.

Період коливань пружинного маятника

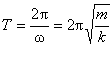.                      (4)

Як видно з формули (4) період і частота коливань пружинного маятника не залежать від прискорення вільного падіння, а визначаються лише масою підвішеного тіла і жорсткістю пружини.

Приклади розв’язування задач

Задача 1. Вантаж масою 400 г здійснює коливання на пружині з жорсткістю 250 Н/м. Амплітуда коливань 15 см. Знайти повну механічну енергію коливань і найбільшу швидкість руху вантажу. Тертям знехтувати.

Згідно з законом збереження механічної енергії,

. За означенням, 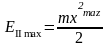, ,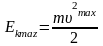тобто

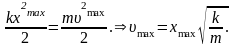
Обчислення:

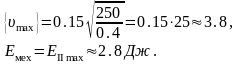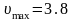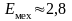Відповідь: м/с, Дж.

Задача 2. Один маятник здійснив 10 коливань, другий за цей же час – 6 коливань. Різниця довжин маятників 16см. Знайти довжини маятників.

Розв’язання

, звідки

Розв’яжемо систему рівнянь:

Задача 3.Точка здійснює гармонічне коливання з частотою n=10 Гц, В момент прийнятий за початковий, точка мала максимальне зміщення А= I мм. Написати рівняння коливань матеріальної точки.

Розв’язання

Рівняння коливань точки можна записати у вигляді x=Asin(ωt+φ) або x=Acos(ωt+φ)(2), де А - амплитуда коливань, ω - циклічна частота, φ - початкова фаза.

Циклічна частота ω пов'язана з частотою співвідношенням ω=2πν

Початкова фаза коливань залежить від форми запису. Якщо використовувати формулу (1), то початкову фазу можна визначити з умови: у момент часу  t=0 X_max=Asinφ₁  звідси φ₁₌arcsin(X_max/A)=arcsin1.

Зміна фази на 2π не змінює стан коливального руху, тому можна прийняти φ₁₌π/2 (5).

При другій формі запису одержуємо: φ₂₌₂πk(6).

З тих же міркувань, що і в першому випадку, знаходимо: φ₂₌₀.

З урахуванням виразів (3) - (6)  рівняння коливань набудуть вигляду X=X_maxsin(2πνt + π/2)

або X=X_maxcos2πνt де X_max=1мм=10^-3м => ν=10Гц.

Задача 4. Матеріальна точка масою m = 5г  здійснює гармонічне коливання із частотою ν= 0,5 Гц. Амплітуда коливань А = 3 см. Визначити: I) швидкість v точки у момент часу, коли зміщення X =1,5 см; 2) максимальну  силу F_max, що діє на точку; 3) повну  енергію E точки, що коливається.