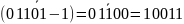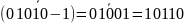Uprościć wyrażenie logic

(A+B+C) (A+B’+C) = (A+C)(B’+B)= A+C

Podać tablicę wartości wyrażenia logicznego

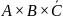
A	B	C	y
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	0
1	0	0	0
1	0	1	0
1	1	0	1
1	1	1	0

Opisać algorytm konwersji liczby naturalnej n z systemu dziesiętnego na dwójkowy

Liczba N = dziewięćdziesiąt dziewięć w postaci dziesiętnej to N₁₀ = 99, poszukujemy jej postaci w systemie dwójkowym.

Kolejne kroki:

1. 99 : 2 = 49, reszta 1 -> 1

2. 49 : 2 = 24, reszta 1 ->11

3. 24 : 2 = 12, reszta 0 ->011

4. 12 ; 2 = 6, reszta 0 ->0011

5. 6 : 2 = 3, reszta 0 -> 00011

6. 3 : 2 = 1, reszta 1 -> 100011

7. 1 : 2 = 0, reszta 1 -> 1100011

Wobec tego 99₁₀ = 1100011₂.

Ogólny algorytm jest następujący:

- dzielimy liczbę N_b przez b, resztę z dzielenia zapisujemy jako pierwszy od lewej znak liczby w systemie o

podstawie b

- wynik dzielenia dzielimy przez b, resztę zapisujemy jak wyżej

- kontynuujemy do chwili gdy wynik dzielenia jest równy zeru.

Podać przykład konwersji liczby 77 z systemu dziesiętnego na szesnastkowy

(77)₁₀ 77:16 reszta z / D Zapis szesnastkowy liczby 77 jest równy 4D 4: 16 4 Dzielimy podobnie jak w poprzednich systemach pamiętając o wartościach jakie przybiera reszta i pamiętając o tym by 10, 11 … zapisywać jako A, B itd

Opisać algorytm tworzenia najczęściej używanej reprezentacji liczby całkowitej ujemnej Liczbę binarną, ujemną bardzo łatwo napisać na papierze, na przykład -11101, trudniej przedstawić w postaci zrozumiałej dla komputera. Wydaje się, że najprościej byłoby dodać jeden bit do binarnego zapisu liczby. Wartość tego dodatkowego bitu umieszczonego na lewo od najbardziej znaczącego bitów liczby naturalnej informowałaby o znaku liczby, na przykład 0 oznaczałoby liczbę dodatnią a 1 liczbę ujemną. Przykład: Dodawanie dwóch liczb jednej dodatniej drugiej ujemnej 0 101001₂ = 41₁₀ > 0, 1 111001₂ = -57₁₀ < 0. Obliczymy sumę tych liczb 0 101001₂ + 1 111001₂ = 1 1100010₂ = -226₁₀. Tymczasem poprawny wynik to 41 - 57 = -16₁₀.

Liczby całkowite ze znakiem

Istnieje kilka innych sposobów reprezentacji ujemnych liczb całkowitych pozbawionych powyższego kłopotu. Bywają przydatne w szczególnych przypadkach. Najczęściej stosowany jest następujący. Do bitów liczby dodajemy bit znaku na lewo od najbardziej znaczącego bitu.

TUTAJ TABLICA

Dodatnią liczbę tworzymy jak powyżej, to znaczy przypisujemy bitowi znaku wartość 0. Liczbę ujemną tworzymy przez zaprzeczenie wszystkich bitów liczby dodatniej (łącznie z bitem znaku) i do wyniku dodajemy liczbę 1. Taka reprezentacja nazywa się kod uzupełnienia dwójkowego (negacja bitów i dodanie 1) (two's complement).

Przykłady

+x2	+x10	- x2	- x10
0 1001	9	1 0110+1=1 0111	-9
0 0001	1	1 1110+1=1 1111	-3
0 0000	0	1 1111+1=1 0000	0
0 1111	15	1 0000+1=1 0001	-15
1 0011	-13		13
	-10		10

Przykład

Liczba 8 bitowa |x| = 11001101, liczba dodatnia x =110101101, liczba ujemna -x = 00110010+1=00110011.

Sprawdzenie: x - x = 0101101+0110011 = 00000000.

Przykład

|x| = 11100011, |y| = 00110001, zaleźć różnicę x - y.

x - y = 011100011 + 011001111 = 000110010, (x - y)₁₀ = +176 ???

x - y = 11100011 - 00110001 = 10110010 = 178₁₀

Sprawdzenie: x₁₀ = 227, y₁₀ = 49, : x₁₀ - y₁₀ = 178.

Dane wprowadzane do komputera oraz wyniki mają między innymi postać liczb naturalnych, całkowitych, ułamkowych i innych.