Все лекции / Лекция 8

Лекция №8 (Задачи 55, 56)

Определение линии пересечения двух поверхностей методом секущих плоскостей

Определение линии пересечения двух многогранников

Многогранниками называют пространственную фигуру, ограниченную отсеками плоскостей, имеющих форму многоугольников.

Определение линии пересечения пирамиды с призмой

Плоский посредник – это вспомогательная плоскость, необходимая для определения точек, принадлежащих линии пересечения поверхностей.

S₂

рёбра

Δ

S₂

Δ

грани

L₂=F₂= M₂=M₂ ^/

M₂=M₂ ^/

Σ₂ ^/

1₂

3₂

5₂

N₂=N₂ ^/

N₂=N₂ ^/

q₂

Θ

2₂

Θ

Σ₂ ^//

E₂=E₂ ^/

B₂

4₂

6₂

E₂=E₂ ^/

A₂

C₂

A₂

B₂

C₂

M₁ ^/

E₁ ^/

M₁ ^/

E₁ ^/

N₁ ^/

L₁

N₁ ^/

A₁

B₁

A₁

B₁

S₁

4₁

6₁

3₁

S₁

1₁

q₁

2₁

q₁

F₁

C₁

C₂

5₁

M₁ ^/

N₁ ^/

M₁ ^/

N₁ ^/

E₁ ^/

E₁ ^/

План решения:

1. Строим точки пересечения рёбер призмы с гранями пирамиды. Для этого используем плоские посредники Σ ^/ и Σ ^// (горизонтальные плоскости уровня).

2. Находим линию пересечения посредника  ^/ с поверхностью пирамиды. Данной линией пересечения является треугольник 1,2,3. Точки пересечения указанного треугольника с ребром М₁ М₁ ^/ определяют точки L и F, принадлежащие линии пересечения. Σ ^/  Δ = q(123).

3. Соединяем точки пересечения рёбер призмы с гранями пирамиды и получаем искомую линию пересечения поверхностей. Определяем видимость линии пересечения и очерков поверхностей.

Определение линии пересечения криволинейных поверхностей методом

секущих плоскостей

Плоский посредник необходимо выбрать таким образом, чтобы данная плоскость пересекала две поверхности или по окружности или по прямым.

Порядок n линии пересечения поверхностей определяется по формуле

n = m_1*m₂;

где m₁ и m₂ – порядки пересекающихся поверхностей.

1)

2)

B₂

B₁

Σ₂^max

Σ₁^max

Σ ^min

Σ₂ ¹

Σ₁

А₂

А₁

1 Посредник – горизонтальная

плоскость уровня Σ₂, n = 2_*2 = 4

2 Посредник – фронтальная

плоскость уровня Σ₂, n = 2_*4 = 8

Σ₁^min

Опорные точки – это экстремальные точки, которые задают граничные посредники, и точки в которых изменяется видимость линии пересечения поверхностей.

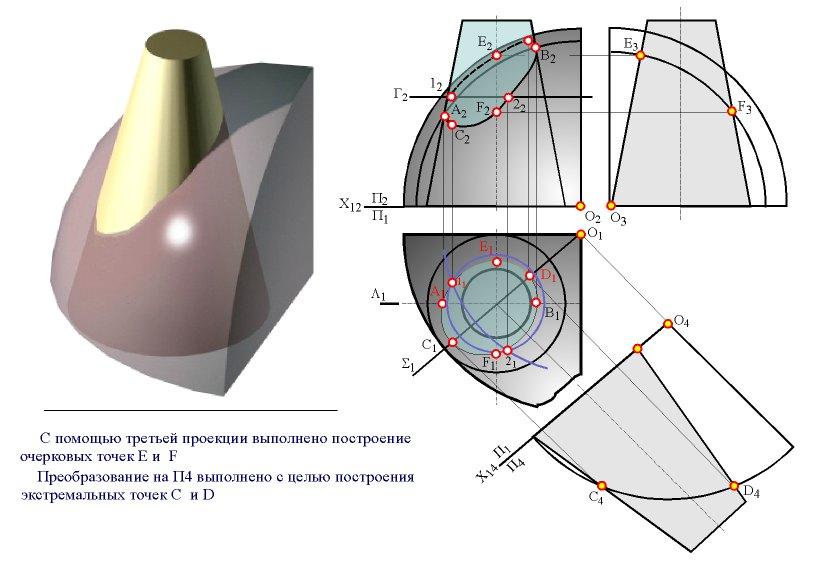
Определение линии пересечения двух поверхностей методом плоского посредника.

Рисунки 4.49 и 4.50

Задача

Заданы поверхность конуса Ф и сферы . Построить линию пересечения поверхностей. Определить видимость линии пересечения и очерков поверхностей.

Δ

Δ

a ^{/ /}

A₂

Σ ^/₂

Σ₂= q₂ ^/ =q₂ ^{/ /}

M₂=N₂

1₂=2₂

Σ₂

Σ ^{/ /}₂

Φ

Φ

B₂

1₁

q₁ ^{/ /}

M₁

B₁

q₁ ^/

N₁

2₁

A₁

План решения:

1. Определяем положение опорных точек A и B – точек пересечения очерков поверхностей на фронтальной проекции. Определяем положение граничных посредников Σ ^{/ /} и Σ ^/.

2. Определяем точки M и N, точки пересечения очерка сферы с поверхностью конуса на горизонтальной проекции. Используем с этой целью вспомогательную плоскость Σ₂. Определяем линии пересечения q₁ ^/ и q₁ ^{/ /}.

Σ₂  Φ = q ^{/ /}

Σ₂  Δ = q ^/

q ^{/ /}  q ^/ = M, N

3. Определяем промежуточные точки 1, 2 … с помощью плоских посредников Σ.

4. Определяем совокупность промежуточных точек, которые соединяем с помощью лекала. Определяем видимость линии пересечения и очерков поверхностей.

Моделирование линий пересечения поверхностей с помощью графической системы КОМПАС

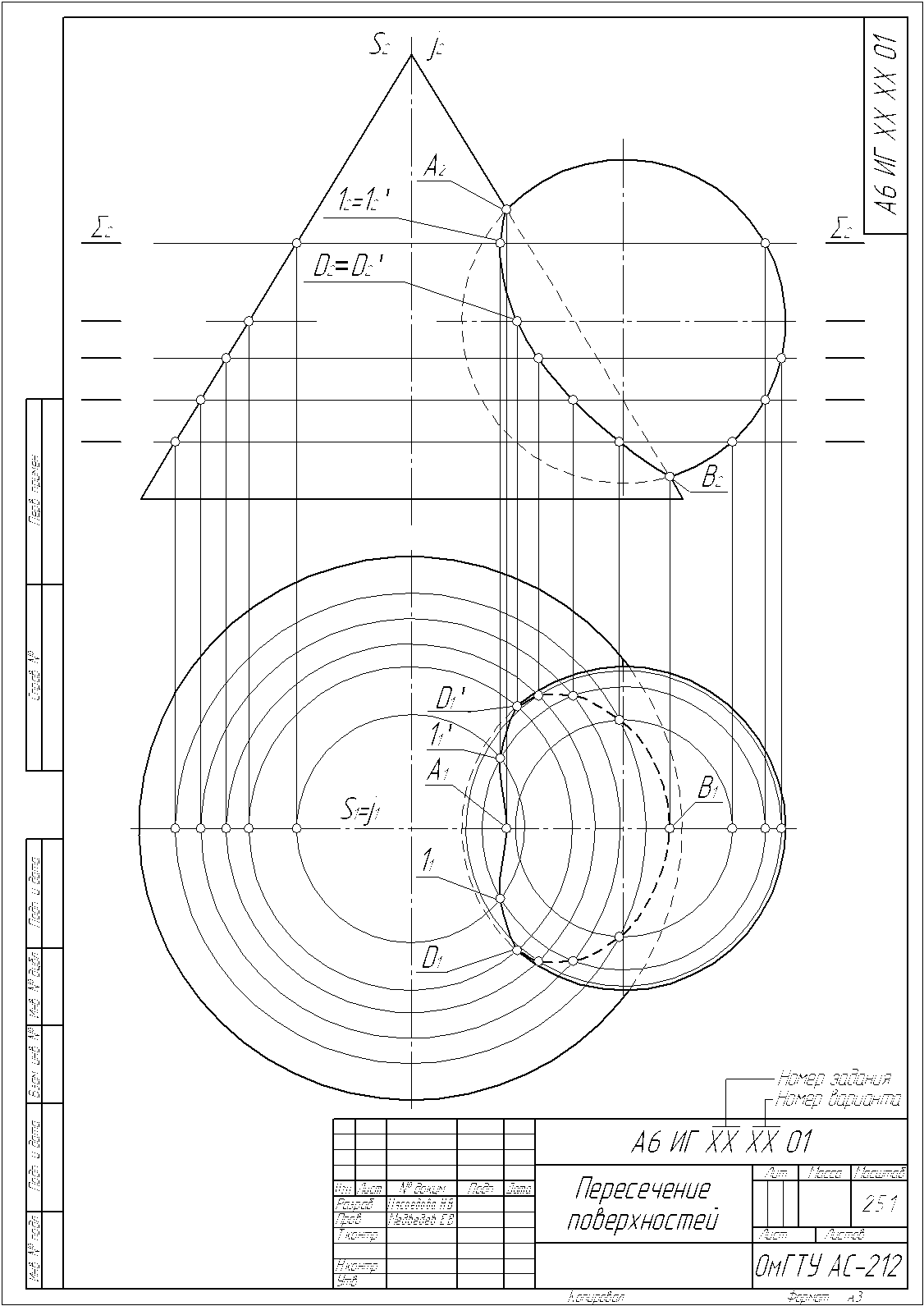
Пересечение поверхностей

(способ секущих плоскостей)

Вариант 1

Задание выполняется на формате А3 (формат располагается вертикально).

Масштаб-2,5:1

Задание: Построить линию пересечения двух заданных поверхностей методом секущих плоскостей. Исходные данные (фронтальная и горизонтальная проекции) приведены ниже (масштаб 1:1).

Методика оформления и последовательность выполнения чертежа «Пересечение поверхностей»:

1. Построить фронтальные и горизонтальные проекции поверхностей тонкими линиями.

2. Построить и обозначить все опорные точки.

3. Выполнить построения промежуточных точек линий пересечения поверхностей по следующему алгоритму:

• Провести плоскость-посредник так, чтобы линии пересечения её с поверхностями были простейшими (прямыми или окружностями).

• Построить линии пересечения плоскости-посредника с исходными поверхностями.

• Определить и обозначить точки пересечения полученных линий.

• Повторить построения минимум четыре раза.

• Соединить полученные точки плавной кривой при помощи лекала.

• Определить видимость линии пересечения и очерков поверхностей на фронтальной и горизонтальной проекциях.