Все лекции / Лекция 4
.docЛекция №4 (Задачи 26, 27, 29, 30)
Взаимное позиционное расположение геометрических фигур.
Параллельность плоскостей
Теорема №1.
Плоскости параллельны, если две пересекающиеся прямые одной плоскости, соответственно параллельны двум пересекающимся прямым другой плоскости.
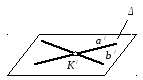
a Σ, b Σ, a ∩ b ,
a / Δ, b / Δ, a / ∩ b /, Δ Σ
a a / , b b / .
Теорема №2.
Плоскости в пространстве параллельны, если на комплексном чертеже их одноимённые следы параллельны между собой.
Δ2, Σ2 – фронтальные следы плоскостей.
Δ2 || Σ2 => Δ || Σ
Задача №1.
Задана плоскость общего положения Σ (a || b) и точка D. Через точку D построить плоскость, параллельную заданной.
a2
b2
l2
n2
m2
b2
а2
12
22
D2
D2
x1,2 2
x1,2 2
a1
D1
a1
D1
l1
b1
b1
l1
11
n1
l1
21
m1
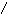
План решения:
1. Строим прямую − l (l∩a , l ∩ b , l Σ);
2. Строим прямую − m. m || a, D m;
3. Строим прямую − n, n || l, D n;
4. Прямые m и n – определяют искомую
плоскость.
П
араллельность
прямой и плоскости
Теорема №3.
Прямая параллельна плоскости, если она параллельна какой-либо прямой, принадлежащей данной плоскости.
m
Σ
l || Σ
l || m
Теорема №4.
Прямая параллельна плоскости в пространстве, если на комплексном чертеже одноименные проекции прямой и следа плоскости параллельны.
Σ2 – фронтальный след плоскости
l2 || Σ 2 => l || Σ
Определение точки пересечения прямой с плоскостью
(1-ая позиционная задача)
1. Плоскость является проецирующей.
Σ2
a2=b2
М2
l2
a2=b2
l2
K2
22
М2
Σ2
x1,2
N2
12
x1,2
N2
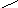
a1
a1
b1
N1
b1
N1
l1
l1
11=21
K1
М1
М1
Точка К (К1,К2) определяется точкой пересечения прямой l2 ∩ Σ2 = K2 проекции l2 со следом плоскости Σ2. Видимость прямой MN определяется с помощью конкурирующих точек 1 и 2.
2.Плоскость является плоскостью общего положения.
а) Решение с заменой плоскостей.
B2
M2
22
2
MN
3
AC
K2
12
h2
C2
A2
N2
32
B1
N1
K1
11
N4
A1
h1
B4
21=31
C1
M1
C4
K4
A4
4
M4
План решения:
1. Используем дополнительную плоскость проекций П4 h, П4 П1. Плоскость, заданная трёугольником ABC, проецируется на плоскость проекций П4 в линию.
2. Находим на П4 точку K4 как точку пересечения проекции прямой N4 M4 со следом плоскости Δ4 .
3. По законам проекционной связи находим проекции точек К1 и К2.
4. Определяем видимость с помощью конкурирующих точек 3 и 2.
б
)
Решение без замены плоскостей. Плоскость
Σ задана
с помощью
двух
параллельных прямых.
K2
Σ
m2
=
Δ2
=
l2
12
22
a2
b2
x1,2
b1
l1
a1
21
K1
m1
11
Посредник – это вспомогательная плоскость, необходимая для решения задач.
План решения:
1. Через прямую l строим вспомогательную фронтально-проецирующую плоскость
Δ2.
2. Находим линию пересечения плоскостей Σ и Δ. Σ ∩ Δ = m (m1,m2)
3. Находим точку пересечения
K1 = l1 ∩ m1.
4. По проекционной связи находим фронтальную проекцию К2.
Определение линии пересечения двух плоскостей
(2-ая позиционная задача)
Σ
M2
Δ
B2
Σ
M2
Δ
B2
Θ
/
12
22
32
42
42
Θ
//
52
82
N2
62
72
m2
n2
A2
C2
A2
C2
n2
x1,2
m2
x1,2
m1
n1
m1
n1
A1
A1
C1
51
61
C1
81
N1
11
21
71
41
B1
31
B1
