Все лекции / Лекция 5

Лекция №5 (Задачи 31, 32, 33, 34)

Перпендикулярность прямой и плоскости. Решение метрических задач, связанных с определением углов между плоскостями и прямой с плоскостью

Прямая перпендикулярная плоскости

Теорема №1

Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, принадлежащим этой плоскости.

a  , b  

l  

a  b = K

l  a

К

l  b

Теорема №2.

Если проекция натуральной величины прямой перпендикулярна следу плоскости, то прямая в пространстве перпендикулярна данной плоскости.

D₂

D₂

B₂

B₂

l₂

C₂

₂

C₂

A₂

₂

A₂

N₂

х_1,2

х_1,2

A₁

A₁

D₁

D₁

N₁

B₁

B₁

l₁

C₁

C₁

l₂  ₂ ,

₂ – фронтальный след плоскости, l  

l₂ – Н.В.

Теорема №3.

Прямая перпендикулярна плоскости, если её горизонтальная проекция перпендикулярна горизонтальной проекции горизонтали, а её фронтальная проекция перпендикулярна фронтальной проекции фронтали.

B₂

B₂

A₂

h₂

2₂

f₂

1₂

A₂

C₂

D₂

l₂

C₂

D₂

х_1,2

х_1,2

A₁

B₁

f₁

B₁

A₁

h₁

2₁

1₁

l₁

C₁

D₁

C₁

D₁

l ^ S

f  S , h  S

l₂  f₂

l₁  h₁

Перпендикулярность двух плоскостей

Теорема №4

Две плоскости взаимно - перпендикулярны, если одна из них содержит прямую, перпендикулярную другой плоскости.

l  Δ

Δ ^ S

l ^ S

Задача №1.

Задана плоскость S (Δ ABC) и прямая общего положения m. Через прямую m провести плоскость, перпендикулярную S.

A₂

B₂

B₂

K₂

m₂

m₂

A₂

h₂

1₂

l₁

l₁

x_1,2

x_1,2

C₂

C₂

K₁

B₁

A₁

B₁

A₁

l₂

h₁

m₁

1₁

m₁

B₄

K₄

C₁

C₁

A₄

₄

C₄

l₄

m₄

x_4,1

План решения.

1. Плоскость ABC с помощью дополнительной плоскостей проекций Π₄ проецируем в линию. Получаем след плоскости S_4. Находим проекцию m₄.

2. Через точку, принадлежащую прямой m₄ проводим l₄  S₄.

3. Находим горизонтальную проекцию прямой l, если известно, что l₄ – Н.В.

4. Прямые l и m определяют искомую плоскость.

У

Δ

гол между плоскостями

l = S  Δ

a  Δ , a  l  ab – угол между плоскостями

b  S , b  l

Для определения угла между двумя плоскостями необходимо обе плоскости S и Δ спроецировать в линии. Для решения данной задачи необходимо линию пересечения данных плоскостей спроецировать в точку.

F₂

F₂

S

S

M₂

M₂

N₂

N₂

E₂

Δ

E₂

Δ

x_1,2

x_1,2

F₁

F₁

M₁

M₁

N₁

N₁

N₄=M₄



E₁

E₁

E₄

x_1,4

План решения

F₄

1. M₁ N₁ – натуральная величина.

2. Используем дополнительную плоскость проекций П₄, перпендикулярную прямой MN. X_4,1  M₁ N₁

3. Получаем следы плоскостей Δ и . Угол  E₄N₄F₄=α определяет искомый угол между двумя плоскостями.  E₄N₄F₄ – искомый угол

E₄ N₄ – след плоскости Δ

F₄ M₄ – след плоскости S

Угол между прямой и плоскостью

Углом между прямой и плоскостью определяет угол между этой прямой и её проекцией на данную плоскость.

АА^/  S , а  S = М

Ð АМА^/ - искомый угол

Задача №2

Определить угол между прямой EF и плоскостью, заданной треугольником ABC.

П

K₅

лан решения.

1. Плоскость ABC проецируем в линию – находим след плоскости – S₄.

2. Находим точку пересечения М₄ проекции прямой l₄ и следа плоскости S₄. М₄ = l₄  S₄.

3. Из точки К₄ опускаем перпендикуляр на след плоскости S₄. Находим основание перпендикуляра. N₄ = n₄  S₄.

4. С помощью Π₅ определяем натуральную величину отрезка прямой K₅M₅ – Н.В.

5. На свободном поле чертежа по гипотенузе и катету определяем Н.В. треугольника MNK, где присутствует искомый угол Ð К ⁰М ⁰ N ⁰.

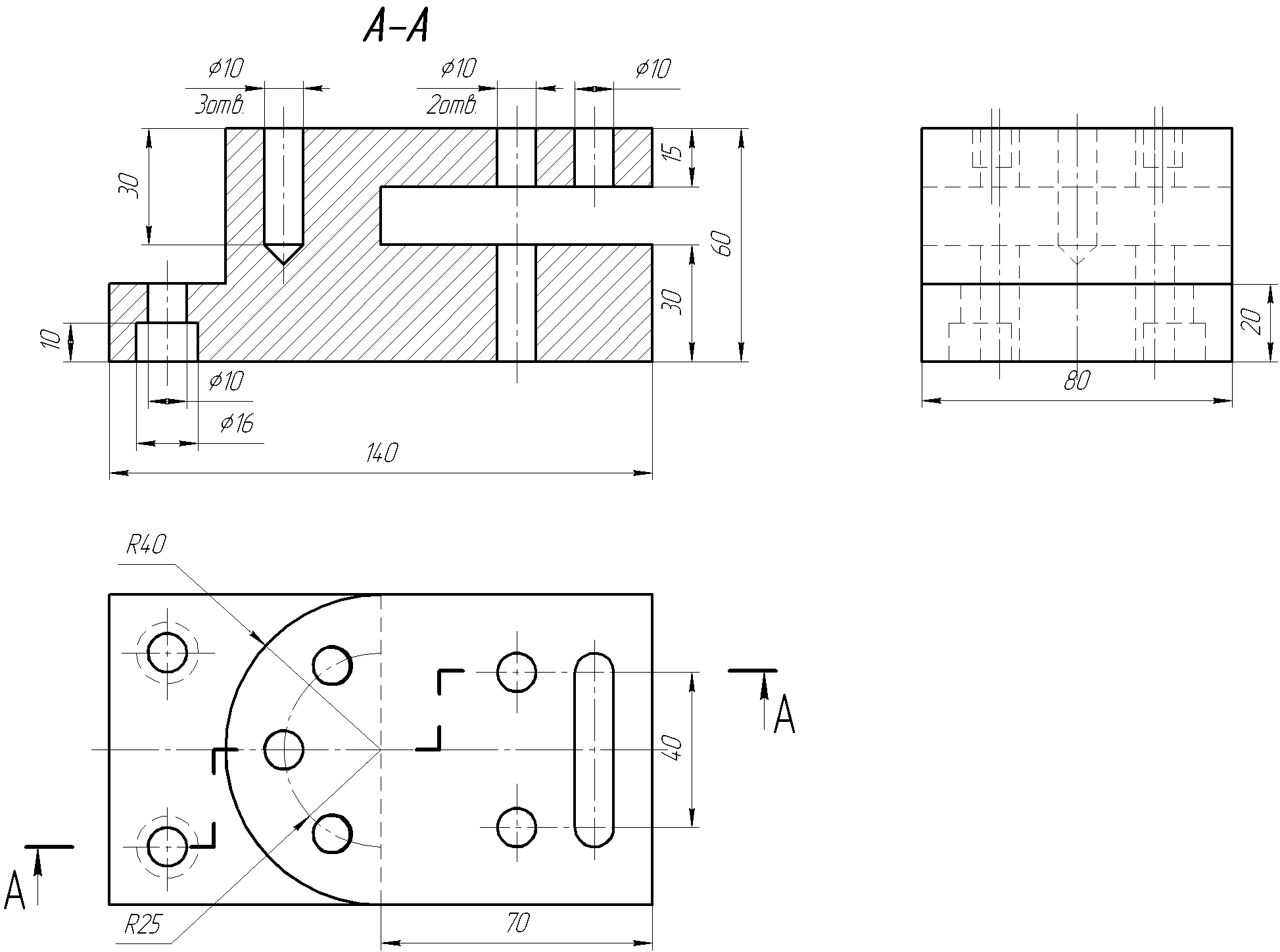
Разрезы ступенчатые

Вариант 1

Задание выполняется на формате А3 (формат располагается горизонтально).

Масштаб-1:1, имея в виду, что исходные данные, выполнены в масштабе 1:2.

Задание: Выполнить ступенчатый разрез предмета, расположив его на месте главного вида или вида сверху. Исходные данные приведены ниже.

М 1:2

Последовательность выполнения и оформления чертежа ступенчатого разреза:

1. Проработать учебную литературу по темам ’Разрезы’ (ГОСТ 2.305-68 раздел 3).

2. Подготовить формат А3. Вычертить рамку чертежа и основной надписи. Произвести компоновку изображений на формате так, чтобы изображения были расположены равномерно на поле чертежа. Расстояние между изображениями, а так же между изображениями и рамкой чертежа, рекомендуется выбрать 40-50мм, что достаточно для нанесения размеров. Вычертить, габаритные прямоугольники для построения трёх видов.

3. По указанным исходным данным (см. изображения выше) начертить главный вид, вид сверху и вид слева. Вычерчивание изображений лучше начинать с вида сверху. Изображения располагаются в проекционной связи.

4. Выполнить на месте трёх изображений необходимые разрезы. Нанести штриховку, обвести изображения. Выполнять разрез рекомендуется в такой последовательности:

а) в определённом месте предмета мысленно провести секущие плоскости;

б) часть предмета, находящуюся между наблюдателем и секущей плоскостью мысленно отбросить;

в) оставшуюся часть предмета спроецировать на фронтальную или горизонтальную плоскость проекций и изобразить на месте вида спереди (или вида сверху).

5. Нанести размеренные линии, проставить размеры.

6. Заполнить основную надпись.

Формирование изображений штриховки в графической системе КОМПАС