Все лекции / Лекция 6

Лекция № 6 (Задачи 42, 43, 46, 47)

Кривые линии, способы задания поверхностей

Кривая – это множество точек пространства, координаты которой являются функциями одной переменной.

Кривую можно задать:

а) Траекторией движения точки.

б) Линией пересечения поверхностей.

Классификация кривых

1. Кривые могут быть пространственными и плоскими.

У плоских кривых все точки принадлежат одной плоскости, в противном случае кривую называют пространственной.

2. Алгебраические кривые – это кривые координаты точек которых удовлетворяют алгебраическому уравнению.

y

a

x

2a

2b

b

3. Трансцендентные кривые – это кривые координаты точек которых удовлетворяют трансцендентному уравнению.

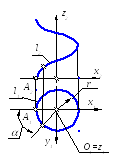
Винтовая линия  l(l₁,l₂) x = r cos

y = r sin 

z = р 

Характеристики алгебраических кривых

1. Порядок – это степень алгебраического уравнения. Геометрически, порядок определяется числом точек пересечения кривой с произвольной прямой.

2. Класс – это число касательных построенных из произвольной точки к заданной кривой.

t, t ^/ - касательные к кривой l.

A, B – точки касания

Дифференциальные характеристики плоских и пространственных кривых

а) плоские кривые

Локальные свойства кривой характеризуются касательной и нормалью.

Касательной называют предельное положение секущей t (t ^/, t ^//, . . .) когда точка М₂ стремится к точке М. Нормаль – это прямая перпендикулярная касательной в данной точке (nt).

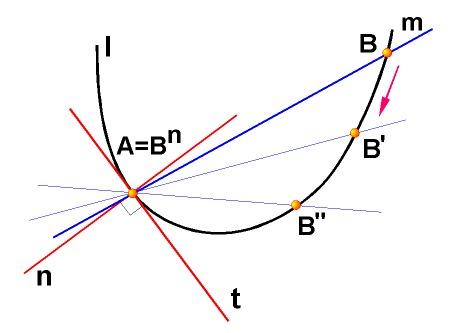
а) пространственные кривые

Локальные свойства пространственной

к

Δ

Σ

ривой характеризуются:

M

Σ – соприкасающейся плоскостью.

Σ



M₂

b

t

M₁

– предельное положение некоторой плоскости определяемой точками M₁, M, M₂ , когда точки M₁ и М₂ стремятся к точке М (M₁→M и М₂→М).

Δ – нормальной плоскостью (перпендикулярная касательной t).

θ – спрямляющаяся плоскость.

Нормальная плоскость Δ перпендикулярна касательной t Δ.

Спрямляющаяся θ плоскость проходит через касательную t, и перпендикулярна соприкасающейся плоскости θ  t,

Дифференциальные свойства пространственных кривых характеризуют:

n – нормаль кривой ;

t – касательная ;

b – бинормаль ;

Задача №1

На комплексном чертеже заданы фронтальная и горизонтальные проекции кривой f. Определить какой является кривая, плоской или пространственной.

f₂

f₂

B₂

C₂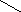

A₂

D₂

K₂

K₂

x_1,2

x_1,2

D₁

K₁

A₁

f₁

B₁

f₁

C₁

План решения:

1. Строим прямые AC и BD пересекающие заданную кривую f.

2. Строим точки пересечения (K₁ и K₂) проекций прямых AC и BD на фронтальной и горизонтальной проекциях.

3. Так как точки пересечения K₁ и K₂ не находятся на одной линии проекционной связи, то кривая a является пространственной.

Способы задания кривых поверхностей

Поверхность – это непрерывное двухпараметрическое множество точек.

1 Задание поверхности с помощью алгебраических уравнений

В этом способе задания поверхность рассматривается как геометрическое множество точек, координаты которых удовлетворяют определенно заданному алгебраическому уравнению. Например, точка A принадлежит поверхности сферы, если её координаты удовлетворяют алгебраическому уравнению:

.

2 Задание поверхности с помощью параметрических уравнений

Точка A определяется параметрическими уравнениями:

где u и v – текущие параметры.

3. Каркасно-кинематический способ

Поверхность представляется линейным каркасом, т.е. совокупностью линий, принадлежащих поверхности, имеющих единый закон образования и связанных определенной зависимостью.

Кривая l в качестве которой выступает эллипс принадлежит плоскости   x , которая перемещается вдоль оси x.

z

Параметры малой и большой полуосей эллипса определяются функциями

, .

Уравнения поверхности

.

Пример задания поверхности линейным каркасом

Понятие об определителе поверхности

Определителем поверхности называется совокупность условий задающих поверхность в пространстве. Определитель поверхности состоит:

1. Из геометрической части.

2. Из алгоритмической части.

Поверхность считается заданной, если можно решить вопрос о принадлежности любой точки пространства заданной поверхности.

Геометрическая часть определителя – совокупность геометрических элементов необходимых для задания поверхности.

Алгоритмическая часть определителя – это совокупность операций (последовательности) по которым строятся образующие (элементы каркаса) поверхности.

m₂

m₂

S₂

1₂

S₂

A₂

l₂

l₂

m

l₁

l₁

– Направляющая поверхности.

l

S₁

m₁

1₁

S₁

m₁

A₁ ^/

– Образующая поверхности.

A₁

S, m  геометрическая часть.

l  S

l  m  алгоритмическая часть.

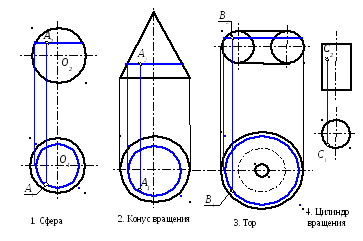
Классификация поверхностей

Поверхности вращения

Построение очерка поверхности вращения

A₁

A₂

A^/

меридиан

Гиперболоид вращения

Создание 3-D моделей в графической системе КОМПАС

с использованием операции вращения

Команда Операция вращения позволяет создать модель детали, представляющее собой тело вращения. Команда доступна, если выделен один эскиз. Для вызова команды необходимо щелкнуть по кнопке (Операция вращения) на инструментальной панели редактирования детали или выберите ее название из меню Операции.

Порядок создания трехмерной модели с использованием операции вращения:

1. Изобразить эскиз вращаемого контура (рис. а).

2. Изобразить осевую линию (осевая линия не должна пересекать вращаемый контур) (рис. 4.5а).

3. Щелкнуть по кнопке операция вращения (рис. б)..

4. Задать в панели свойств угол поворота (рис. в).

5. Щелкнуть по кнопке создать объект.

11