8. Векторная алгебра

Если известны координаты точек и, то координаты вектора

Разложение этого вектора по ортам :

Длина вектора находится по формуле а направляющие косинусы равныОрт вектора

Пример 8. Даны точки

Разложить вектор по ортами найти его длину, направляющие косинусы, орт вектора. Найдем координаты векторов:

и

Вектор

Контрольные варианты к задаче 8. Даны точки А, В и С. Разложить вектор по ортамНайти длину, направляющие косинусы и орт вектора.

1.		2.
3.	.	4.
5.		6.
7.		8.
9.		10.
11.		12.
13.		14.
15.		16.
17.		18.
19.		20.
21.		22.
23.		24.
25.		26.
27.		28.
29.		30.

Задача 9. Если даны векторы то.

Тогда; проекция векторана направление вектора, условие перпендикулярности ненулевых векторов выглядит следующим образом:

Условие коллинеарности векторов: .

Пример 9. Даны вершины треугольника Найти угол при вершине А и проекцию векторана сторону АС. С

Внутренний угол при вершине А образован векторами,

А В

Тогда

Проекция на направление вектора:

Контрольные варианты к задаче 9

1. Даны векторы иНайти

2. Найти косинус угла, образованного вектором и осьюOZ.

3. Даны векторы и .Найти косинус угла между диагоналями параллелограмма, построенного на векторах .

4. Даны векторы и . Вычислить

5. Найти косинус угла, образованного вектором и осью ОУ.

6. Даны векторы и .Найти косинус угла, образованного вектором и осью ОХ.

7. Даны векторы и .Найти

8. Вычислить проекцию вектора на ось вектора .

9. Определить угол между диагоналями параллелограмма, построенного на векторах и .

10. Определить, при каком значении m векторы иперпендикулярны.

11. Определить, при каком значении векторы и взаимно перпендикулярны.

12. Даны вершины треугольника: . Определить внутренний угол при вершине В.

13. Даны вершины треугольника: . Определить внутренний угол при вершине А.

14. Найти вектор , коллинеарный векторуи удовлетворяющий условию

15. Даны две точки иВычислить проекцию вектора на ось вектора

16. Даны векторы: и . Вычислить

17. Найти острый угол между диагоналями параллелограмма, построенного на векторах , .

18. Даны три вектора: ,,. Найти

19. Даны три вектора: ,,. Найти

20. Найти острый угол между диагоналями параллелограмма, построенного на векторах и

21. Даны три вектора: ,,. Вычислить

22. Найти вектор , зная, что он перпендикулярен векторами

и удовлетворяет условию

23. Найти вектор , коллинеарный векторуи удовлетворяющий условию

24. Даны вершины треугольника: Определить внешний угол при вершине А.

25. Даны вершины треугольника: Определить внешний угол при вершине А.

26. Дан вектор и точкииНайти

27. В треугольнике с вершинами Определить внутренний угол при вершине А.

28. Даны векторы иНайти проекцию векторана направление вектора

29. Даны вершины треугольника: Найти проекцию векторана сторону

30. Даны векторы Найти проекцию вектора на вектор

Задача 10. Площадь параллелограмма, построенного на векторах

можно найти по формуле а площадь треугольника, построенного

на этих векторах:

Пример 10. Даны вершины треугольника Найти его площадь и длину высоты, опущенной из вершины С.

. Находим векторы

Векторное произведение

Так как гдедлина высоты, опущенной из вершины С на сторону АВ,.

Контрольные варианты к задаче 10

1. В параллелограмме ABCD даны векторы иНайти площадь параллелограмма, построенного на диагоналях параллелограмма

ABCD.

2. Даны три вершины параллелограмма ,,. Найти длину высоты, опущенной из вершины С (через площадь

параллелограмма).

3. Найти площадь треугольника с вершинами , ,

(средствами векторной алгебры).

4. Найти площадь треугольника с вершинами , ,(средствами векторной алгебры).

5. Даны три вершины треугольника: ,,. Найти его высоту, приняв ВС за основание (через площадь треугольника).

6. На векторах ипостроен параллелограмм. Найти

площадь параллелограмма, сторонами которого являются диагонали данного параллелограмма.

7. Даны векторы и. Найти векторперпендикулярный к векторамесли модуль векторачисленно равен площади треугольника, построенного на векторахи тройка векторовлевая.

8. Даны точки ,, Найти площадь параллелограмма, построенного на векторах и ().

9. На векторах ипостроен параллелограмм. Найти высоту, опущенную на основание(через площадь).

10. В треугольнике ABC, где ,найти длину высоты, опущенной на сторонуAB (через площадь треугольника; средствами векторной алгебры).

11. На векторах ипостроен параллелограмм. Найти площадь параллелограмма, построенного на диагоналях данного параллелограмма.

12. В треугольнике с вершинами , и точка E делит сторону АВ пополам. Найти площадь треугольника АСЕ (средствами векторной алгебры).

13. Найти площадь параллелограмма со сторонами если

14. Найти площадь треугольника со сторонами если,

и

15. Дан треугольник с вершинами , и . Вычислить площадь треугольника и высоту, опущенную из вершины А (средствами векторной алгебры).

16. Даны векторы иНайти вектор, который пер-

пендикулярен векторам , если длина его численно равна площади треуго-

льника, построенного на векторах , и тройка векторовправая.

17. Даны точки ,и . Вычислить площадь треугольника и высоту, опущенную из вершины С (средствами векторной алгебры).

18. В треугольнике с вершинами , и точка E делит сторону АВ пополам. Найти площадь треугольника ВСЕ (средствами векторной алгебры).

19. Даны точки ,и . Найти площадь параллелограмма, построенного на векторах и

20. Даны три вершины треугольника: ,,. Вычислить его высоту, опущенную из вершины В (через площадь, средствами векторной алгебры).

21. Дан треугольник с вершинами , и . Найти его высоту, опущенную из вершины А (через площадь, средствами векторной алгебры).

22. Даны векторы иВычислить площадь треугольника, построенного на векторах

23. Даны векторы иВычислить площадь треугольника, построенного на векторах

24. Найти площадь параллелограмма, построенного на векторах где

25. В треугольнике с вершинами , и точка E делит сторону АВ пополам. Найти площадь треугольника АСЕ (средствами векторной алгебры).

26. Даны векторы иНайти вектор, который перпендикулярен векторамесли модуль векторачисленно равен площади треугольника, построенного на векторах, и тройка векторовлевая.

27. Даны точки , и . Найти длину высоты треугольника АВС, опущенной из вершины С (через площадь, средствами векторной алгебры).

28. Даны три вершины параллелограмма ,и. Найти длину высоты, опущенной из вершины С (через площадь, средствами векторной алгебры).

29. На векторах ипостроен параллелограмм. Найти площадь параллелограмма, построенного на его диагоналях.

30. Даны векторы ,иВычислить площадь треугольника, построенного на векторах

Задача 11. Если даны координаты , то смешанное произведение векторов вычисляют по формуле

.

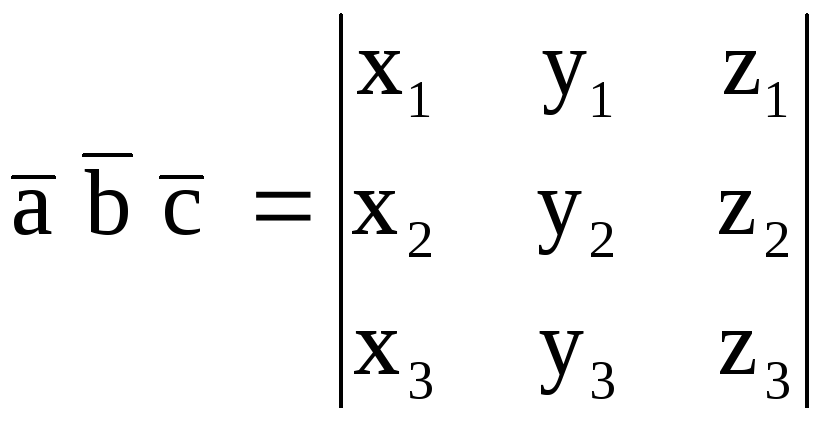Объемы параллелепипеда и тетраэдра (треугольной пирамиды), построенных на векторах находятся с помощью смешанного произведения векторов:

,

Если > 0, то тройка векторов - правая.

Если < 0, то тройка левая.

Если = 0, то векторы компланарны.

Пример 11. Дан параллелепипед построенный на векторахиНайти высоту, проведенную из вершинына граньABCD.

Объем равен произведению площади основания на высоту:

находится также по формуле , поэтому

.

Вычислим векторное произведение =

Тогда