Физика / 2

Теоретические вопросы:

1. Сформулируйте закон сохранения механической энергии. В чём заключается его физическая сущность?

2. Приведите формулу момента силы относительно неподвижной точки в векторном и скалярном виде.

3. Какова связь между потенциальной энергией и силой?

4. Дайте определение момента импульса.

Тест:

1. Формула кинетической энергии:

1. 

2. 

3. 

2. Какие значения принимает кинетическая энергия:

1. Только положительна

2. Только отрицательна

3. Положительна и отрицательна

3. В потенциальных полях действуют:

1. Диссипативные силы

2. Консервативные силы

3. Все перечисленное

4. Абсолютно неупругими называются тела, для которых коэффициент восстановления

1. 

2. 

3. 

5. Теорема Штейнера:

1. 

2. 

3. 

6. При абсолютно упругом соударении:

1. Сохраняется механическая энергия тел

2. Тела при столкновении движутся как одно целое

3. Коэффициент восстановления равен 0

7. Мощность измеряется в:

1. Дж

2. Вт

3. Кл

8. Формула деформирующей силы:

1. 

2. 

3. 

9. Кому принадлежит идея закона сохранения механической энергии?

1. Ломоносову

2. Ньютону

3. Штейнеру

10. Формула элементарной работы:

1. 

2. 

3. 

Задачи:

№1: Получите формулу для момента инерции однородного шара J, который имеет радиус R и массу m по отношению к оси, которая проходит через его центр масс.

Решение:

Разобьем весь шар на элементарные массы. Такой массой будет диск радиуса r, на расстоянии h от диска, который проходит через центр масс шара.

Причем

Момент инерции для элемента массы запишем как:

где для рассматриваемого диска имеем:

(где – плотность шара, V – его объём, dh – высота рассматриваемого диска)

Тогда элементарный момент инерции равен:

Для того, чтобы найти момент инерции всего шара, относительно оси, которая проходит через его центр масс возьмем интеграл по объему шара:

Ответ:

№2:По горизонтальной плоскости катится диск со скоростью . Определить коэффициент сопротивления, если диск, будучи предоставленным самому себе, остановился, пройдя путь S=18м.

Дано: СИ

k - ?

Решение:

Так как диск катится, он будет вращаться с угловой скоростью и двигаться поступательно со скоростью .

(где R – радиус диска)

Тогда 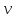равно:

Кинетическая энергия вращения равна:

, где и

(J – момент инерции сплошного диска)

Тогда

Помимо вращения существует поступательное движение со скоростью . Тогда кинетическая энергия поступательного движения равна

Тогда полная кинетическая энергия равняется

Когда диск катится, на него действует сила трения равная

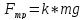
(где k – коэффициент сопротивления)

Работа сил трения равна

Тогда

Ответ: