
Физика / 1
.docx-
Когда в любой замкнутой электрической цепи, в которой протекает электрический ток, наблюдается явление самоиндукции:
-
Только при замыкании цепи
-
Только при размыкании цепи
-
При размыкании или замыкании цепи
-
Какова единица измерения индуктивности?
-
Дж
-
Гн
-
Н
-
Магнитное поле создается:
-
Электрическим зарядом
-
Любым телом
-
Движущимся электрическим зарядом
-
Какова единица измерения индукции магнитного поля?
-
Тл
-
Вб
-
В
-
Кто открыл явление электромагнитной индукции?
-
А. Ампер
-
Ш. Кулон
-
М. Фарадей
-
Сила, с которой магнитное поле действует на проводник с током, называется:
-
Силой тока
-
Силой Ампера
-
Магнитной индукцией
-
Изменяясь во времени, магнитное поле пораждает:
-
Вихревое электрическое поле
-
Постоянное магнитное поле
-
Электростатическое поле
Задачи:
№1. За 5 мс магнитный поток, пронизывающий контур, убывает с 9 до 4 мВб. Найти ЭДС индукции в контуре.
 Дано:
СИ
Дано:
СИ



 -?
-?
Решение:
По формуле Фарадея-Максвелла:
 ,
где
,
где
 величина
электродвижущей силы (ЭДС), Ф- магнитный
поток, t- время.
величина
электродвижущей силы (ЭДС), Ф- магнитный
поток, t- время.

Ответ:

№2. Найти скорость изменения магнитного потока в соленоиде из 2000 витков при возбуждении в нем ЭДС индукции 120 В.
 Дано:
СИ
Дано:
СИ
n = 2000,
ε = 120 B.
 -?
-?
Решение:
По формуле закона электромагнитной индукции на случай соленоида с N витками имеет вид:
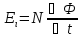 ,
где (
,
где ( величина
электродвижущей силы (ЭДС), Ф- магнитный
поток, t- время, N-
количество витков)
величина
электродвижущей силы (ЭДС), Ф- магнитный
поток, t- время, N-
количество витков)

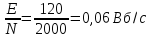
Ответ: 0,06Вб/с
Лекция №12 (Григорьева)
Теоретические вопросы:
-
Уравнение Максвелла
-
В чем заключается закон полного тока?
-
Что изучает термодинамика?
-
Что такое ток смещения
Тест:
1.В интегральном виде второе уравнение Максвелла (Теорема о циркуляции магнитного поля) представлено следующим образом:
-
 =
=

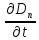 )
ds
)
ds
-
 =
=

 )
ds
)
ds
-
 =
=

 )
ds
)
ds
2.Чем определяется поток электрической индукции через произвольную замкнутую поверхность внутри этой поверхности?
-
Ионом
-
Зарядом
-
Количеством электронов
3. закон Гаусса для индукции магнитного поля:
-
 ,
d
,
d =1
=1 -
 ,
d
,
d =0
=0 -
 ,
d
,
d =-1
=-1
4. Скорость света в вакууме:
-
Зависит от скорости движения источника и наблюдателя
-
Не зависит от скорости движения источника и наблюдателя
-
Не зависит от скорости движения источника, но зависит от наблюдателя
5. Все физические процессы протекают:
-
Одинаково в различных инерциальных системах отсчета при одинаковых начальных условиях.
-
Одинаково в различных инерциальных системах отсчета при различных начальных условиях.
-
Различно в одинаковых инерциальных системах отсчета при одинаковых начальных условиях
6. формула вектора Умова – Пойнтинга:
7. полная плотность энергии электромагнитной волны равна:
-
 +
+

-
 +
+

-
 +
+

8. Скорость электромагнитной волны в вакууме (воздухе):
-
с =

-
с =
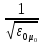
-
с =

(где ε0 — электрическая постоянная, μ0 — магнитная постоянная).
9. Плоская электромагнитная волна - электромагнитная волна, в которой всем точкам, лежащим в любой плоскости, перпендикулярной направлению ее распространения, соответствуют:
-
Одинаковые напряженности электрических или магнитных полей.
-
Различные напряженности электрических или магнитных полей.
-
Одинаковые напряженности электрических, и разных магнитных полей.
10. Условием возникновения электромагнитных волн является:
-
Замедленное движение электрических зарядов.
-
Ни от чего не зависит.
-
Ускоренное движение электрических зарядов.
Задачи:
№1. Из системы уравнений Максвелла получить уравнения непрерывности токов и закон сохранения заряда.

 Дано:
СИ:
Дано:
СИ:
rot =
=



Ур-я
непрерывности токов - ? З-н сохранения
зарядов - ?
Решение:
Используем уравнение:
rot =
=

 (а)
(а)
Проведем
для него операцию дивергенции (div или
 ).
Получим:
).
Получим:



 )=
)=
 (
(


 )
(b)
)
(b)
из системы уравнений Максвелла знаем, что
 =
4
=
4 (c)
(c)
Подставим (с) в (b) получим:
0=
 (
(


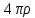 )
)
отсюда
следует 0=
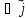 +
+


или в интегральной форме:

Соответственно для замкнутых изолированных областей получим:
 =0
,
=0
,

Это уравнение непрерывности для тока, содержащее в себе закон сохранения заряда – один из фундаментальных принципов, который подтверждается экспериментом.
Ответ:
 =0
,
=0
,

№2. Доказать, что сумма токов проводимости и тока смещения, сцепленных с контуром, действительно непрерывна и, следовательно, полный ток, сцепленный с любым контуром, не зависит от выбора поверхности, натянутой на этот контур.


 Дано:
СИ:
Дано:
СИ:
Доказать:
 =
=
Доказательство: допустим, что в произвольном магнитном поле на некоторый контур натянуты две произвольные поверхности S1 и S2.

Знак
вектора потока
 ,
сцепленного с контуром, связывается
правилом правого винта с направлением
обхода контура L. В частности, при том
направлении силовых линий, которое
изображено на поток D сцепленный, с
контуром для поверхностей, S1 и S2 нужно
считать положительным. Рассмотрим
замкнутую полость, ограниченную
поверхностью S1 + S2. В соответствии с
теоремой Гаусса для нее можно записать
уравнение:
,
сцепленного с контуром, связывается
правилом правого винта с направлением
обхода контура L. В частности, при том
направлении силовых линий, которое
изображено на поток D сцепленный, с
контуром для поверхностей, S1 и S2 нужно
считать положительным. Рассмотрим
замкнутую полость, ограниченную
поверхностью S1 + S2. В соответствии с
теоремой Гаусса для нее можно записать
уравнение:
 d
d =
q
(a)
=
q
(a)
Здесь q — сумма зарядов, попадающих в рассматриваемую полость, ограниченную поверхностью S1 + S2. Продифференцируем обе части этого уравнения по времени:
 (
(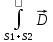 d
d )=
)=
 (b)
(b)
Преобразуем раздельно левую и правую части этого уравнения. Поток вектора D сквозь замкнутую поверхность можно представить следующим образом:
 d
d =
= d
d +
+
 d
d )
(c)
)
(c)
Линии векторного поля D входят в замкнутую полость через поверхность S_2. По определению они создают отрицательный поток. Если рассматривать поток, сцепленный с контуром, то, используя правило знаков, его необходимо считать положительным. Следовательно, выражение (c) применительно к контуру, можно записать так:
 d
d =
=
 -
-
 (d)
(d)
Уясним, что собой представляет правая часть уравнения (b). Производная от полного заряда, заключенного в полости, стоящая в правой части (b), показывает, на какую величину изменяется заряд в полости в секунду. За счет чего может изменяться заряд в полости? В силу закона сохранения заряда он может изменяться только за счет неравных токов входящих и выходящих из нее. Пpи равенстве этих токов полный заряд в полости оставался бы постоянным. Причём, токи, входящие в полость, следует считать положительными (они увеличивают заряд в полости), а токи, выходящие из нее, — отрицательными. Таким образом, уравнение (b) можно представить следующим образом:
 -
-
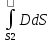 =
-
=
- +
+

или
 =
=
Что и требовалось доказать.
Лекция №13 (Мохова)
Теоретические вопросы :
-
Основные принципы корпускулярно-волнового дуализма
-
Что такое монохроматическая волна?
-
Что такое интерференция?
-
Какие волны можно назвать когерентными?
Тест:
-
Кто был приверженцем корпускулярной теории света
-
Мария Склодовская-Кюри
-
Исаак Ньютон
-
Леонардо Да Винчи
-
Согласно этой теории свет – это поток частиц, идущих от источника во все стороны
-
Корпускулярная теория
-
Волновая теория
-
Молекулярная теория
-
Как называется явление усиления или ослабления света при наложении световых пучков друг на друга
-
Преломление
-
Дифракция
-
Интерференция
-
Выберите верное утверждение
-
Скорость света в воде меньше, чем в вакууме.
-
Скорость света в воде больше, чем в вакууме.
-
Скорость света в воде такая же, как в вакууме.
-
Когерентные волны можно получить с помощью
-
отражения волны
-
преломления волны
-
разделения волны с помощью двух щелей
-
Что наблюдается в центре интерференционных колец Ньютона в проходящем белом свете?
-
Темное пятно
-
Белое пятно
-
Фиолетовое пятно
-
Выберите значение наиболее близкое к скорости света в вакууме
-
300 000 000 км/ч
-
340 м/с
-
300 000 км/с
-
Два когерентных источника с длиной волны λ расположены на разных растояниях
 и
и
 от точки A
( см рис). В точке А наблюдается…
от точки A
( см рис). В точке А наблюдается…
-
Интерференционный максимум
-
Интерференционный минимум
-
Ничего
-
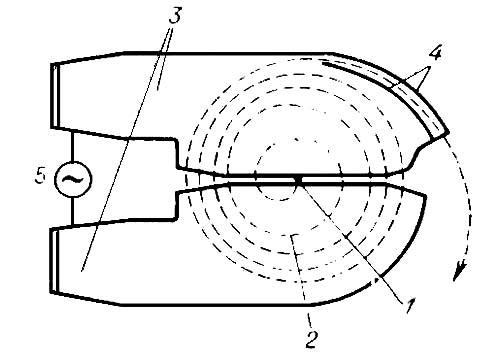
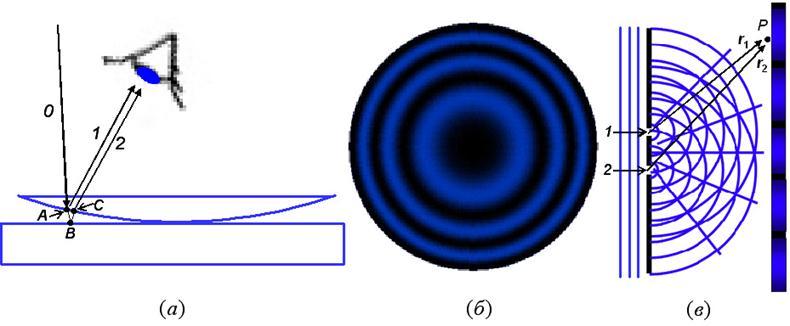
На каком рисунке изображено схематическое устройство интерферометра Майкельсона?
1)
2)

3)
-
Кому из ученых принадлежит открытие интерференции света?
-
Александр Попов
-
Томас Юнг
-
Генрих Герц
Задачи:
№1: В опыте Юнга расстояние 𝓁 от щелей до экрана равно 3 м. Определить
угловое расстояние между соседними светлыми полосами, если третья светлая полоса на экране отстоит от центра интерференционной картины на расстоянии 4,5 мм
|
|
Дано: 𝓁=3м
m=3 |
СИ:
4.5· |
|
|
|
|
|
|||
|
|
ϕ=? |
|
||
|
|
|
|||
Решение:

Из рисунка видно, что
 (1),
(1),
Где △x - расстояние между двумя соседними
максимумами (или минимумами), называемое шириной интерференционной полосы, равно
△x= (2).
(2).
Максимумы интенсивности
будут наблюдаться в случае
 =m
=m ,
где m=0,1,2,…(3).
,
где m=0,1,2,…(3).
Выразим
из (3)

 и подставим в (2). Тогда получим
и подставим в (2). Тогда получим
△x= (4).
(4).
Подставим (4) в (1):
tgϕ= (5).
(5).
Так
как 𝓁>>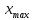 , то угол
, то угол
 очень мал. Тогда tgϕ
~ ϕ.Значит,
(5) запишем так
очень мал. Тогда tgϕ
~ ϕ.Значит,
(5) запишем так
ϕ=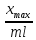 (6)
(6)
Вычислим ϕ:
ϕ= =5·
=5· рад.
рад.
Ответ:
5· рад.
рад.
|
Дано: λ=0,6 мкм R=4м r=1,8 мм м=2 |
СИ: 6·
1.8· |
|
|
|
Решение: В проходящем свете оптическая разность хода, при условии, что параллельный пучок света падает нормально на плоскую поверхность линзы, △=2dn
или n=
По теореме Пифагора
Когда радиус кривизны R линзы большой, d очень мал. Тогда (2) перепишем в виде
Условие максимума в проходящем свете
Подставим (3) и (4) в (1): n= Вычислим n:
n= Ответ: 1,48
Лекция №14(Эбергард) Теоретические вопросы:
Тест.
1) Теплопроводность 2) Дифракция 3) Диффузия
1) Принцип Гюйгенса-Френеля 2) Принцип Паули 3) Закон всемирного тяготения
1) Плотность 2) Среднюю длину свободного пробега молекул 3) Радиус k-ой зоны Френеля для плоской волны
1)Номер зоны Френеля 2)Коэффициент диффузии 3)Длина волны
1)Первый закон Ньютона 2)Первый закон термодинамики 3)Закон отражения
1)Преломленный луч лежит в одной плоскости с падающим лучом и нормалью, восстановленной в точке падения; отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных веществ 2)Силы, с которыми тела взаимодействуют друг с другом, равны по модулю и направлены вдоль одной прямой в противоположные стороны 3)Отраженный луч лежит в одной плоскости с падающим лучом и нормалью, восстановленной в точке падения; угол падения равен углу отражения
1)Увеличение числа щелей не влияет на главные максимумы 2)Увеличение числа щелей приводит к росту интенсивности главных максимумов и к уменьшению их ширины 3)Увеличение числа щелей приводит к уменьшению интенсивности главных максимумов и к увеличению их ширины
где φ- 1)Длина волны 2)Угол между нормалью к поверхности решетки и направлением дифрагированных волн 3)Номер главного максимума
1)Для освещения наблюдения областей, недоступных для обычного видения; в различных оптико-электронных приборах, обрабатывающих информацию; в фотокопирующих системах; в медицине. 2)Для тушения возгорания нефтепродуктов, горючих материалов, горючих жидкостей, а также для тушения возгорания электроустановок. 3)Для всего вышеперечисленного. Задачи. №1:На диафрагму с круглым отверстием радиусом r=1 мм падает нормально параллельный пучок света длиной волны λ=0,05 мкм. На пути лучей, прошедших через отверстие, помещают экран. Определить максимальное расстояние bmax от центра отверстия до экрана, при котором в центре дифракционной картины еще будет наблюдаться темное пятно.
Решение: Расстояние, при котором будет видно темное пятно, определяется числом зон Френеля, укладывающихся в отверстии. Если число зон четное, то в центре дифракционной картины будет темное пятно. Число зон Френеля, помещающихся в отверстии, убывает по мере удаления экрана от отверстия. Наименьшее четное число зон равно двум. Следовательно, максимальное расстояние, при котором еще будет наблюдаться темное пятно в центре экрана, определяется условием, согласно которому в отверстии должны поместиться две зоны Френеля. Из
рисунка следует, что расстояние от
точки наблюдения O
на экране до края отверстия на 2
По
теореме Пифагора получим:
Учтя,
что
Произведя вычисления по последней формуле, найдем bmax=1 м Ответ: bmax=1 м.
№2:
На
щель шириной а=0,1
мм нормально падает параллельный
пучок света от монохроматического
источника (λ=0,6 мкм). Определить ширину
l
центрального максимума в дифракционной
картине, проецируемой с помощью линзы,
находящейся непосредственно за
щелью, на экран, отстоящий от линзы
на расстоянии L=l
м
Решение:
Максимум
интенсивности света занимает
область между ближайшими от него
справа и слева минимумами
интенсивности. Поэтому ширину
центрального максимума интенсивности
примем равной расстоянию между этими
двумя минимумами интенсивности
Минимумы
интенсивности света при дифракции от
одной щели наблюдаются под углами φ,
определяемыми условием
где
k
—
порядок минимума; в нашем случае равен
единице.
Расстояние между двумя
минимумами на экране определим
непосредственно по чертежу:
Выразим sin φ из формулы (1) и подставим его в равенство (2):
Произведя вычисления по формуле (3), получим l=1,2 см. Ответ: l=1,2 см Лекция №15 (Головкина) Теоретические вопросы:
Тест:
Где:
Где:
Где:
2)
3)
где
где
где
Задачи: №1:Какова
скорость света в кристалле каменной
соли, если угол Брюстера при падении
пучка света из воздуха составляет
Дано:
с = ?
Решение:В
качестве основы для решения задачи
используем закон Брюстера:
Выразим абсолютный показатель преломления кристалла каменной соли из выражения (1) и имеем:
Показатель преломления света в кристалле связан со скоростью распространения света в нем как:
Где: c - скорость света в вакууме. Приравняем правые части выражений (2) и (3), получим:
Выразим
из (4) искомую скорость
Проведем
вычисления, зная, что для воздуха
Ответ:
1,94* №2: Рассчитать молярную концентрацию тирозина в растворе, если известно, что плотность поглощения (D) электромагнитного излучения с длиной волны λмакс. = 275 нм такого раствора в кювете толщиной l =10 см составляет 13.4, а молярный коэффициент поглощения ε = 13400 л /(моль . см).
Дано: СИ λмакс. = 275 нм 275. 10-9 l =10 см 0,1 м D = 13,4 ε = 13400 л /(моль . см) Cm = ?
Решение: Уравнение Бугера –Ламберта –Бера: D = ε . CM . l, Откуда:
Ответ:
Лекция №16 (Мохова) Теоретические вопросы:
Тест:
Задачи: №1. Определить наибольшую длину света, при которой может происходить фотоэффект для пластины, при Авых. = 8,5*10-19 Дж.
Авых. = 8,5*10-19 Дж
max-?
Решение: Так как нам требуется определить только наибольшую длину света, при которой может происходить фотоэффект, то кинетической энергией электрона можно пренебречь. Так как нам требуется найти длину волны, то выражаем её, зная, что c = *.
Выражая
из полученной формулы длину волны,
получаем:
=
После вычислений получаем ответ: = 2,34*10-7 м. Ответ: = 2,34*10-7 м
Дано: СИ
= 5*10-7 м
E-?
Решение:
Так
как нам требуется найти энергию фотона,
то используем формулу E
= h.
Но вместо частоты нам дана длина волны,
поэтому, выражая частоту через отношение
скорости света к длине волны, формула
приобретает следующий вид: E
=
После вычислений получаем ответ: E = 3,98*10-19 Дж. Ответ: E = 3,98*10-19 Дж.
Лекция №17 (Харченко) Теоретические вопросы:
Тест:
Задачи: №1. С космического корабля, удаляющегося от Земли со скоростью 0,7c, стартует ракета в направлении движения корабля. Скорость ракеты относительно Земли равна 0,96с. Чему равна скорость ракеты относительно космического корабля? (с – скорость света)
Решение: Пусть
По закону релятивистского сложения скоростей --
--
получаем:
Ответ: 0,8c №2.
Определить угол θ рассеяния фотона
после соударения со свободным
электроном, если изменение длины волны
(∆λ) при рассеянии равно 3,62 пм (
Решение:
Ответ: 120⁰
Лекция №18 (Харченко) Теоретические вопросы
Тест 1. Если А – работа выхода, h – постоянная Планка, то длина волны света λкр, соответствующая красной границе фотоэффекта, определяется соотношением 1) A/h 2) h/A 3) hc/A 2.Явление отклонения от прямолинейного распространения волн, отгибание волнами препятствий, называют… 1)Дисперсией 2)Интерференцией 3)Дифракцией 3.Главное условие наблюдения интерференции и дифракции света. Волны должны быть 1)Когерентными 2)Синфазными 3)Монохроматическими 4. Явление сложения волн в пространстве, приводящее к перераспределению энергии волн в пространстве, называется… 1)Поляризацией 2)Интерференцией 3)Дифракцией 5.Л. де Бройль утверждал, что волновыми свойствами обладают… 1) Фотоны 2)Электроны 3)Все частицы материи 6.К микрочастицам относят… 1)Электроны, протоны и др. простые частицы 2)Атомы, ядра и др. сложные частицы 3)Все вышеперечисленное 7.Установка для опыта Дэвиссона и Джермера включала в себя… 1)Монокристалл никеля, чувствительный гальванометр 2)Цилиндр Фарадея, монокристалл никеля 3)Чувствительный гальванометр, монокристалл никеля и цилиндр Фарадея 8.Волновая функция- функция, используемая… 1)В квантовой механике 2)В волновой оптике 3)В геометрической оптике 9.Волновая функция удовлетворяет условия нормировки, если {\displaystyle {\int \limits _{V}{\Psi ^{\ast }\Psi }dV}=1}
1)10 2)1 3)7 10.Корпускулярно-волновые свойства микрочастиц открыл… 1) Девиссон 2) Шредингер 3) Де Бройль
Задачи. №1: Какую энергию необходимо дополнительно сообщить электрону. Чтобы его дебройлевская длина волны уменьшилась от 100 до 50пм? Решение:
Энергия электрона равна
Учитывая,
что
Ответ: №2: Какую разность потенциалов должен пройти электрон, чтобы его дебройлевская длина волны была равна его комптоновской длине волны? Решение:
Работа кинетического поля численно
равна кинетической энергии, приобретенной
электроном при прохождении ускоряющей
разности потенциалов:
Кинетическую
энергию электрона найдем из условия
Преобразуем
предыдущее выражение и решим получившееся
квадратное уравнение относительно
Комптоновская
длина волны электрона
Учитывая,
что
Тогда
Значит,
Ответ: 0,21 МВ
Лекция №19 (Головкина) Теоретические вопросы:
Тест:Начало формы
Задачи: №1:Электрон находится в бесконечно глубоком одномерном прямоугольном потенциальном ящике шириной l. Вычислить вероятность того, что электрон, находящийся в возбужденном состоянии (n=2), будет обнаружен в средней трети ящика. Решение: Вероятность W обнаружить частицу в интервале х1 < х < х2 определяется равенством
W
=
где Ψn(x)- нормированная собственная волновая функция, отвечающая данному состоянию. Нормированная собственная волновая функция, описывающая состояние электрона в потенциальном ящике, имеет вид
Ψn(x)= Возбужденному состоянию (n=2) отвечает собственная функция
Ψ2(x)= Подставив Ψ2(x) в подынтегральное выражение формулы (1) и вынося постоянные величины за знак интеграла, получим
W=
Согласно
условию задачи, х1=
=
Заметив,
что
Ответ: W= 0.195
U(x) I II Рис.
46.1
U0 x
Низкая потенциальная ступень
Е=100 эВ 4% отр-ся U0 = ?
Решение: Коэффициент отражения ρ от низкой потенциальной ступени выражается формулой
ρ= где К1 и К2 – волновые числа, отвечающие движению электронов в областях I и II (см. рис. 46.1) В области I кинетическая энергия электрона Е равна и волновое число
К1
=
Поскольку координата электрона не определена, то импульс электрона определяется точно и, следовательно, в данном случае можно говорить о точном значении кинетической энергии. В области II кинетическая энергия электрона равна E – U0 и волновое число
К2
=
Коэффициент отражения может быть записан в виде
ρ
= (
Разделим
числитель и знаменатель дроби на
ρ
= (
Решая
уравнение относительно
Возведя обе части равенства в квадрат, найдем высоту потенциальной ступени:
U0
= ( 1-
Подставив сюда значения величин и производя вычисления, найдем U0 = 55.6 эВ Ответ: U0 = 55.6 эВ
Лекция №20 (Харченко) Теоретические вопросы
Тест
1)n = 1, l = 0, ml = 0 2)n = 1, l = 1, ml = 1 3)n = 1, l = 1, ml = 0
1)сплошные 2)полосатые 3)клетчатые
1)
2)
3)
1) -ihdY/dx = pxY 2) Y = const·exp(i/hpxx)
3)
1) Е ≈ Еэл + Екол + Евращ 2) Е ≈ Еэл + Екол 3) Е ≈ Евращ
1)
2)
3)
1)оператор Гамильтона 2)оператор Лапласа 3)оператор Лаймана
2)колебательно-вращательные 3)электронно-вращательные
1)геометрическую форму орбитали 2)энергетический уровень электрона 3)ориентация орбитали в пространстве
1) потенциальной энергии 2) полной энергии системы 3) кинетической энергии
Задачи №1.
Рассматривая
молекулу как квантовый гармонический
осциллятор, находящийся в основном
состоянии (n=0),
найти амплитуду А классических
колебаний, выразив её через параметр
Решение. В точках наибольшего отклонения в классической механике скорость частицы равна 0, а её полная энергия равна потенциальной
Где
Ответ:
№2. Охарактеризовать квантовыми числами внешние электроны атома кислорода в основном состоянии. Ответ представить в виде таблицы. Решение. Электронная формула атома кислорода: 1s22s22p4. Во внешнем слое у этого атома находятся 6 электронов 2s22p4. Значения их квантовых чисел приведены в таблице.
n-главное квантовое число l-орбитальное квантовое число
Лекция № 21(Головкина) Теоретические вопросы:
Тест:
где: L – значение орбитального момента атома S - значение спинового момента атома J - значение полного момента
где: L – значение орбитального момента атома S - значение спинового момента атома J - значение полного момента
где: L – значение орбитального момента атома S - значение спинового момента атома J - значение полного момента
Задачи №1:В опыте Штерна атомы серебра, вылетающие с поверхности раскаленной нити, проходят через щель внутреннего цилиндра и оседают на охлажденной стенке наружного цилиндра (рис. 67). Когда система цилиндров приводится в быстрое вращение, изображение щели смещается. Прибор вращается сначала в одну сторону, а затем в другую. При этом расстояние, измеренное между смещенными изображениями щели, равно ∆l = 2,66 мм. Найдите скорость атомов, если радиусы внутреннего и внешнего цилиндров 2 и 8 см, скорость вращения цилиндров 283 с-1.
Дано: СИ
Решение:
за время
а цилиндр на это время поворачивается на угол
Где:
Тогда
Ответ:
№2:Какова
мультиплетность состояния атома (τ),
если максимальная величина проекции
магнитного момента атома в состоянии
Дано:
τ = ? Решение : В качестве основы для решения задачи применим формулу:
Из условий задачи:
Найдем:
Мы знаем, что по условию задачи L=2 J=2, используем формулу фактора Ланде, выразим квантовое число S:
Найдем мультиплетность:
Ответ:
|




 =4.5мм
=4.5мм м
м м
м м
м =?
=? (1)
(1)
 +
+ =
=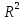 ;
; =
= ;
; =2Rd-
=2Rd- (2).
(2). =2Rd
или d=
=2Rd
или d= (3).
(3). ,…(4)
,…(4)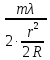 =
=
 (5).
(5). ≈1,48.
≈1,48.



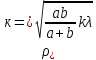 2)
2) 3)
3)
 ,
где
,
где
 -
-
 ,
k=0,1,2,3,…,
,
k=0,1,2,3,…,
 больше, чем расстояние bmax.
больше, чем расстояние bmax.
 <<
<< и что членом, содержащим
и что членом, содержащим
 ,
можно пренебречь, последнее равенство
перепишем в виде
,
можно пренебречь, последнее равенство
перепишем в виде


 (1)
(1) .
Заметив, что при малых углах
.
Заметив, что при малых углах ,
перепишем эту формулу в виде
,
перепишем эту формулу в виде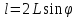 (2)
(2) (3)
(3) ,
,
 -
интенсивность падающего на поляризатор
света,
-
интенсивность падающего на поляризатор
света, )
- интенсивность света, выходящего из
поляризатора.
)
- интенсивность света, выходящего из
поляризатора. =
=
 ,
,
 –
амплитуда
световой волны
–
амплитуда
световой волны =
=
 ,
,
 –
амплитуда
световой волны
–
амплитуда
световой волны


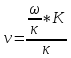 ,
, -
волновое
число
-
волновое
число – частота
– частота =
=
 ,
,
 – частота
– частота =
= ,
,
 – частота
– частота ,
где
,
где
 =
=
 ;
;
 – угол падения
– угол падения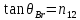 ,
где
,
где
 =
=
 ;
;
 – угол падения
– угол падения ,
где
,
где
 =
=
 ;
;
 – угол падения
– угол падения
 ?
?


 (1)
(1) =
=
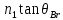 (2)
(2) =
=
 (3)
(3) (4)
(4) ,
получим:
,
получим:
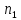 =
1, c
= 3*
=
1, c
= 3* .
.








 Дано:
СИ
Дано:
СИ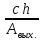 ,
где c
– скорость света, равная 3*108
м/с, h
– постоянная Планка, равная 6,63*10-34
Дж*с.
,
где c
– скорость света, равная 3*108
м/с, h
– постоянная Планка, равная 6,63*10-34
Дж*с.

 №2.
Найти энергию фотона, если известно,
что длина волны данного фотона равна
5*10-7
м.
№2.
Найти энергию фотона, если известно,
что длина волны данного фотона равна
5*10-7
м. ,
где c
– скорость света, равная 3*108
м/с, h
– постоянная Планка, равная 6,63*10-34
Дж*с.
,
где c
– скорость света, равная 3*108
м/с, h
– постоянная Планка, равная 6,63*10-34
Дж*с.








 )
)





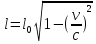





 Дано:
СИ
Дано:
СИ


 -?
-? – скорость корабля относительно
Земли,
– скорость корабля относительно
Земли,
 – скорость ракеты относительно
корабля, а
– скорость ракеты относительно
корабля, а
 -- скорость ракеты относительно Земли,
тогда
-- скорость ракеты относительно Земли,
тогда
 ,
а
,
а


 (
(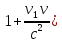 ,
далее:
,
далее:
 ,
и
,
и
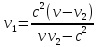 = 0,8c
= 0,8c )
) Дано:
СИ
Дано:
СИ



 -?
-? ,
где h
– постоянная Планка, m
– масса фотона, а с – скорость света
,
где h
– постоянная Планка, m
– масса фотона, а с – скорость света → θ
= 120⁰
→ θ
= 120⁰

 –длина волны де Бройля для электрона,
получим
–длина волны де Бройля для электрона,
получим




 :
:



 ,импульс такого электрона равен
,импульс такого электрона равен


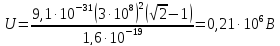
 =
-
=
-
 *
* +UΨ
+UΨ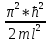 n2
(n=1,
2, 3, ….)
n2
(n=1,
2, 3, ….) *(px-Et)]
*(px-Et)] *(Е-U)Ψ=0
*(Е-U)Ψ=0 n2
(n=1,
2, 3, ….)
n2
(n=1,
2, 3, ….) *(px-Et)]
*(px-Et)]

 =
-
=
-
 *
* +UΨ
+UΨ *(Е-U)Ψ=0
*(Е-U)Ψ=0
 *(px-Et)]
*(px-Et)] )
)


 )
) =
-
=
-
 *
* +UΨ
+UΨ =
-
=
-
 *
*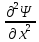 +UΨ
+UΨ )
) *(px-Et)]
*(px-Et)]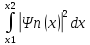 ,
(1)
,
(1) *
* *x
*x *
* *x
(2)
*x
(2)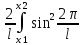 xdx.
(3)
xdx.
(3) l
и х2
=
l
и х2
=
 l.
Подставим эти пределы интегрирования
в формулу (3), произведем замену
l.
Подставим эти пределы интегрирования
в формулу (3), произведем замену
 *x
=
*x
=
 (1-
(1- x)
и разобьем интеграл на два:
x)
и разобьем интеграл на два: W=
W=
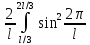 xdx=
xdx=
 (
(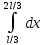 -
-
 )
=
)
=
 (
(
 -
-
 x
l/3
2l/3
)=
x
l/3
2l/3
)=
 -
-
 (
( -
-
 ).
). =
=
 ,
а
,
а
 = -
= -
 ,
получим W=
0.195
,
получим W=
0.195



 Е
Е

 Дано:
Дано:

 .
. )2
)2 :
: )2
)2 , получим
, получим =
=

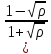 )2
)*E
)2
)*E






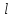 ?
? .
.


 ,
,

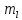 -магнитное
квантовое число
-магнитное
квантовое число
 -спиновое
квантовое число
-спиновое
квантовое число
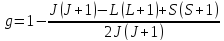 ,
,
 ,
, ,
,
 см 0,02
м
см 0,02
м  мм
2,66*10-3
м
мм
2,66*10-3
м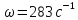

 см.
При вращении цилиндров атомы серебра
проходят расстояние
см.
При вращении цилиндров атомы серебра
проходят расстояние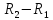
 ,
, ,
, -
расстояние, на которое смещается
изображение щели
-
расстояние, на которое смещается
изображение щели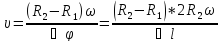


 равна
равна
 .
.






