Физика / 12

Теоретические вопросы:

1. Уравнение Максвелла

2. В чем заключается закон полного тока?

3. Что изучает термодинамика?

4. Что такое ток смещения

Тест:

1.В интегральном виде второе уравнение Максвелла (Теорема о циркуляции магнитного поля) представлено следующим образом:

1. = ) ds

2. = ) ds

3. = ) ds

2.Чем определяется поток электрической индукции через произвольную замкнутую поверхность внутри этой поверхности?

1. Ионом

2. Зарядом

3. Количеством электронов

3. закон Гаусса для индукции магнитного поля:

1. , d=1

2. , d=0

3. , d=-1

4. Скорость света в вакууме:

1. Зависит от скорости движения источника и наблюдателя

2. Не зависит от скорости движения источника и наблюдателя

3. Не зависит от скорости движения источника, но зависит от наблюдателя

5. Все физические процессы протекают:

1. Одинаково в различных инерциальных системах отсчета при одинаковых начальных условиях.

2. Одинаково в различных инерциальных системах отсчета при различных начальных условиях.

3. Различно в одинаковых инерциальных системах отсчета при одинаковых начальных условиях

6. формула вектора Умова – Пойнтинга:

1. 

2. 

3. 

7. полная плотность энергии электромагнитной волны равна:

4. +

5. +

6. +

8. Скорость электромагнитной волны в вакууме (воздухе):

1. с =

2. с =

3. с =

(где ε₀ — электрическая постоянная, μ₀ — магнитная постоянная).

9. Плоская электромагнитная волна - электромагнитная волна, в которой всем точкам, лежащим в любой плоскости, перпендикулярной направлению ее распространения, соответствуют:

1. Одинаковые напряженности электрических или магнитных полей.

2. Различные напряженности электрических или магнитных полей.

3. Одинаковые напряженности электрических, и разных магнитных полей.

10. Условием возникновения электромагнитных волн является:

1. Замедленное движение электрических зарядов.

2. Ни от чего не зависит.

3. Ускоренное движение электрических зарядов.

Задачи:

№1. Из системы уравнений Максвелла получить уравнения непрерывности токов и закон сохранения заряда.

Дано: СИ:

rot=

Ур-я непрерывности токов - ?

З-н сохранения зарядов - ?

Решение:

Используем уравнение:

rot= (а)

Проведем для него операцию дивергенции (div или ). Получим:

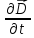)= ( ) (b)

из системы уравнений Максвелла знаем, что

= 4 (c)

Подставим (с) в (b) получим:

0= ( )

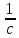отсюда следует 0= +

или в интегральной форме:

Соответственно для замкнутых изолированных областей получим:

=0 ,

Это уравнение непрерывности для тока, содержащее в себе закон сохранения заряда – один из фундаментальных принципов, который подтверждается экспериментом.

Ответ: =0 ,

№2. Доказать, что сумма токов проводимости и тока смещения, сцепленных с контуром, действительно непрерывна и, следовательно, полный ток, сцепленный с любым контуром, не зависит от выбора поверхности, натянутой на этот контур.

Дано: СИ:

Доказать:

=

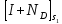Доказательство: допустим, что в произвольном магнитном поле на некоторый контур натянуты две произвольные поверхности S1 и S2.

Знак вектора потока , сцепленного с контуром, связывается правилом правого винта с направлением обхода контура L. В частности, при том направлении силовых линий, которое изображено на поток D сцепленный, с контуром для поверхностей, S1 и S2 нужно считать положительным. Рассмотрим замкнутую полость, ограниченную поверхностью S1 + S2. В соответствии с теоремой Гаусса для нее можно записать уравнение:

d= q (a)

Здесь q — сумма зарядов, попадающих в рассматриваемую полость, ограниченную поверхностью S1 + S2. Продифференцируем обе части этого уравнения по времени:

(d)= (b)

Преобразуем раздельно левую и правую части этого уравнения. Поток вектора D сквозь замкнутую поверхность можно представить следующим образом:

d =d + d) (c)

Линии векторного поля D входят в замкнутую полость через поверхность S_2. По определению они создают отрицательный поток. Если рассматривать поток, сцепленный с контуром, то, используя правило знаков, его необходимо считать положительным. Следовательно, выражение (c) применительно к контуру, можно записать так:

d = - (d)

Уясним, что собой представляет правая часть уравнения (b). Производная от полного заряда, заключенного в полости, стоящая в правой части (b), показывает, на какую величину изменяется заряд в полости в секунду. За счет чего может изменяться заряд в полости? В силу закона сохранения заряда он может изменяться только за счет неравных токов входящих и выходящих из нее. Пpи равенстве этих токов полный заряд в полости оставался бы постоянным. Причём, токи, входящие в полость, следует считать положительными (они увеличивают заряд в полости), а токи, выходящие из нее, — отрицательными. Таким образом, уравнение (b) можно представить следующим образом:

- = - +

или

=

Что и требовалось доказать.