
Физика / 19
.docxЛекция №19 (Головкина)
Теоретические вопросы:
-
Что такое потенциальная яма?
-
Что такое одномерный потенциальный порог?
-
Что из себя представляет коэффициент прохождения?
-
Что такое волновая функция?
Тест:Начало формы
-
Потенциальная энергия U частицы, находящейся в одномерной бесконечно глубокой потенциальной яме, удовлетворяет одному из условий:
-
U >0
-
U <0
-
U =0
-
Одномерное временное уравнение Шредингера:
-
iћ*
 =
-
=
-
 *
* +UΨ
+UΨ -
 *(Е-U)Ψ=0
*(Е-U)Ψ=0 -
Еn=
 n2
(n=1,
2, 3, ….)
n2
(n=1,
2, 3, ….) -
Ψ(x;у)= А*exp [
 *(px-Et)]
*(px-Et)]
-
Собственное значение энергии частицы, находящейся на n-ом энергетическом уровне в бесконечно глубоком одномерном прямоугольном потенциальном ящике:
-
 *(Е-U)Ψ=0
*(Е-U)Ψ=0 -
Еn=
 n2
(n=1,
2, 3, ….)
n2
(n=1,
2, 3, ….) -
Ψ(x;у)= А*exp [
 *(px-Et)]
*(px-Et)] -
Ψn(x)=
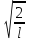 *
* *x
*x
-
Какая потенциальная ступень называется низкой:
-
если высота U0 больше энергии Е частицы
-
если высота U0 равна энергии Е частицы
-
если энергия Е частицы больше высоты U0
-
если энергия Е равна 0
-
Какая потенциальная энергия называется высокой:
-
если энергия Е равна 0
-
если высота U0 равна энергии Е частицы
-
если энергия Е частицы больше высоты U0
-
если высота U0 больше энергии Е частицы
-
Чему равен коэффициент прохождения волн де Бройля:
-
ρ=

-
τ =

-
Ψn(x)=
 *
* *x
*x -
iћ*
 =
-
=
-
 *
* +UΨ
+UΨ
-
Чему равен коэффициент отражения волн де Бройля:
-
 *(Е-U)Ψ=0
*(Е-U)Ψ=0 -
ρ=

-
Ψ(x;у)= А*exp [
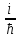 *(px-Et)]
*(px-Et)] -
τ =

-
Чему равен коэффициент прозрачности прямоугольного потенциала ступени конечной ширины:
-
D ≈ exp(-
 )
) -
τ=

-
Ψn(x)=
 *
* *x
*x -
ρ=

-
Каким равенством определяется вероятность нахождения частицы в интервале х1 < х < х2 :
-
 *(Е-U)Ψ=0
*(Е-U)Ψ=0 -
W =

-
D ≈ exp(-
 )
) -
iћ*
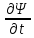 =
-
=
-
 *
* +UΨ
+UΨ
-
Чему равна волновая функция, описывающая одномерное движение свободной частицы:
-
iћ*
 =
-
=
-
 *
* +UΨ
+UΨ -
D ≈ exp(-
 )
) -
Ψ(x;у)= А*exp [
 *(px-Et)]
*(px-Et)] -
W =

Задачи:
№1
Электрон находится в бесконечно глубоком одномерном прямоугольном потенциальном ящике шириной l. Вычислить вероятность того, что электрон, находящийся в возбужденном состоянии (n=2), будет обнаружен в средней трети ящика.
Решение:
Вероятность W обнаружить частицу в интервале х1 < х < х2 определяется равенством
W
=
 ,
(1)
,
(1)
где Ψn(x)- нормированная собственная волновая функция, отвечающая данному состоянию.
Нормированная собственная волновая функция, описывающая состояние электрона в потенциальном ящике, имеет вид
Ψn(x)= *
* *x
*x
Возбужденному состоянию (n=2) отвечает собственная функция
Ψ2(x)= *
* *x
(2)
*x
(2)
Подставив Ψ2(x) в подынтегральное выражение формулы (1) и вынося постоянные величины за знак интеграла, получим
W=
 xdx.
(3)
xdx.
(3)
Согласно
условию задачи, х1= l
и х2
=
l
и х2
=
 l.
Подставим эти пределы интегрирования
в формулу (3), произведем замену
l.
Подставим эти пределы интегрирования
в формулу (3), произведем замену
 *x
=
*x
=
 (1-
(1-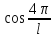 x)
и разобьем интеграл на два:
x)
и разобьем интеграл на два:
 W=
W=
 xdx=
xdx=
 (
( -
-
 )
=
)
=
 (
(
 -
-
 x
l/3
2l/3
)=
x
l/3
2l/3
)=
=
 -
-
 (
( -
-
 ).
).
Заметив,
что
 =
=
 ,
а
,
а
 = -
= -
 ,
получим W=
0.195
,
получим W=
0.195
Ответ: W= 0.195
№2
U(x)
II I
Рис.
46.1

U0 x


Низкая потенциальная ступень
 Дано:
Дано:
Е=100 эВ
4% отр-ся
U0 = ?
Решение:
Коэффициент отражения ρ от низкой потенциальной ступени выражается формулой
ρ=
где К1 и К2 – волновые числа, отвечающие движению электронов в областях I и II (см. рис. 46.1)
В области I кинетическая энергия электрона Е равна и волновое число
К1
=

Поскольку координата электрона не определена, то импульс электрона определяется точно и, следовательно, в данном случае можно говорить о точном значении кинетической энергии.
В области II кинетическая энергия электрона равна E – U0 и волновое число
К2
=
 .
.
Коэффициент отражения может быть записан в виде
ρ
= (
 )2
)2
Разделим
числитель и знаменатель дроби на
 :
:
ρ
= (
 )2
)2
Решая
уравнение относительно
 , получим
, получим
 =
=

Возведя обе части равенства в квадрат, найдем высоту потенциальной ступени:
U0
= ( 1-
 )2
)*E
)2
)*E
Подставив сюда значения величин и производя вычисления, найдем
U0 = 55.6 эВ
Ответ: U0 = 55.6 эВ
