Физика / 14

Лекция 14

Теоретические вопросы:

1. Что такое дифракция волн?

2. Сформулируйте принцип Гюйгенса.

3. Что такое волновод?

4. Что изображено на рисунке?

Тест.

1. Какое явление представлено на рисунке?

1) Теплопроводность 2) Дифракция 3) Диффузия

2. Основной постулат волновой теории, описывающий и объясняющий механизм распространения волн, в частности, световых (а)

1) Принцип Гюйгенса-Френеля 2) Принцип Паули 3) Закон всемирного тяготения

3. Что выражает представленная формула?

1) Плотность 2) Среднюю длину свободного пробега молекул 3) Радиус k-ой зоны Френеля для плоской волны

4. Формула радиуса k-ой зоны Френеля для сферической волны (а) 1) 2) 3)

5. Разрешающая сила дифракционной решетки: (в)

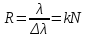, где -

1)Номер зоны Френеля 2)Коэффициент диффузии 3)Длина волны

6. Закон, согласно которому отраженный луч лежит в одной плоскости с падающим лучом и нормалью, восстановленной в точке падения; угол падения равен углу отражения.

1)Первый закон Ньютона 2)Первый закон термодинамики 3)Закон отражения

7. Закон преломления

1)Преломленный луч лежит в одной плоскости с падающим лучом и нормалью, восстановленной в точке падения; отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных веществ 2)Силы, с которыми тела взаимодействуют друг с другом, равны по модулю и направлены вдоль одной прямой в противоположные стороны 3)Отраженный луч лежит в одной плоскости с падающим лучом и нормалью, восстановленной в точке падения; угол падения равен углу отражения

8. При помощи рисунка сформулируйте зависимость изменения главных максимумов при увеличении числа щелей решетки

1)Увеличение числа щелей не влияет на главные максимумы 2)Увеличение числа щелей приводит к росту интенсивности главных максимумов и к уменьшению их ширины 3)Увеличение числа щелей приводит к уменьшению интенсивности главных максимумов и к увеличению их ширины

9. Условие главных максимумов интенсивности

, k=0,1,2,3,…,

где φ-

1)Длина волны 2)Угол между нормалью к поверхности решетки и нап­равлением дифрагированных волн 3)Номер главного макси­мума

10. Для чего применяются световоды?

1)Для освещения наблюдения областей, недоступных для обычного видения; в различных оптико-электронных приборах, обрабатывающих информацию; в фотокопирующих системах; в медицине. 2)Для тушения возгорания нефтепродуктов, горючих материалов, горючих жидкостей, а также для тушения возгорания электроустановок. 3)Для всего вышеперечисленного.

Задачи.

№1:На диафрагму с круглым отверстием радиусом r=1 мм падает нормально параллельный пучок света длиной волны λ=0,05 мкм. На пути лучей, прошедших через отверстие, помещают экран. Определить максимальное расстояние b_max от центра от­верстия до экрана, при котором в центре дифракционной картины еще будет наблюдаться темное пят­но.

Дано: r=1мм λ=0,05 мкм

bmax-?

Решение: Расстояние, при котором будет видно темное пят­но, определяется числом зон Фре­неля, укладывающихся в отвер­стии. Если число зон четное, то в центре дифракционной картины бу­дет темное пятно.

Число зон Френеля, помещаю­щихся в отверстии, убывает по мере удаления экрана от отверстия. Наименьшее четное число зон равно двум. Следовательно, максимальное расстояние, при котором еще будет наблюдаться темное пятно в центре экрана, определяется условием, согласно которому в отверстии должны поместиться две зоны Френеля.

Из рисунка следует, что расстояние от точки наблюдения O на экране до края отверстия на 2 больше, чем расстояние b_max.

По теореме Пифагора получим:

Учтя, что << и что членом, содержащим , можно пренеб­речь, последнее равенство перепишем в виде

Произведя вычисления по последней формуле, найдем

b_max=1 м

Ответ: b_max=1 м.

№2: На щель шириной а=0,1 мм нормально падает параллельный пучок света от монохроматического источника (λ=0,6 мкм). Определить ширину l центрального максимума в дифракционной картине, проецируемой с помощью линзы, нахо­дящейся непосредственно за щелью, на экран, отстоящий от лин­зы на расстоянии L=l м

Дано: a=0,1 мм λ=0,6 мкм L=1 м
l-?

Решение: Максимум интенсивности света за­нимает область между ближайшими от него справа и слева миниму­мами интенсивности. Поэтому ширину центрального максимума интенсивности примем равной расстоянию между этими двумя минимумами интенсивности Минимумы интенсивности света при дифракции от одной щели наблюдаются под углами φ, определяемыми условием (1)

где k — порядок минимума; в нашем случае равен единице. Расстояние между двумя минимумами на экране определим не­посредственно по чертежу: . Заметив, что при малых уг­лах

, перепишем эту формулу в виде

(2)

Выразим sin φ из формулы (1) и подставим его в равенство (2):

(3)

Произведя вычисления по фор­муле (3), получим

l=1,2 см.

Ответ: l=1,2 см