Вопросы к экзамену по математике 2 курс.

1. Понятие комплексного числа. Действие над комплексными числами.

Ко́мпле́ксные чи́сла — числа вида  , где   и   — вещественные числа,   — мнимая единица (величина, для которой выполняется равенство:  ). Множество всех комплексных чисел с арифметическими операциями является полем и обычно обозначается   от лат. complex — тесно связанный.

Суммой двух комплексных чисел z₁=х₁+iy₁ и z₂=х₂+iy₂ называется комплексное число, определяемое равенством

z₁+z₂=(x₁+x₂)+i(y₁+y₂).                             (28.1)

Сложение комплексных чисел обладает переместителъным (коммутативным) и сочетательным (ассоциативным) свойствами:

• z₁+z₂=z₂+z₁

• (z₁+z₂)+z₃=z₁+(z₂+z₃).

Из определения (28.1) следует, что геометрически комплексные числа складываются как векторы (см. рис. 164).

28.2 Вычитание комплексных чисел

Вычитание определяется как действие, обратное сложению. Разностью двух комплексных чисел z1 и z2 называется такое комплексное число z, которое, будучи сложенным с z2, дает число zl т. е. z=z1-z2, если z+z2=z1.

Если z1=x1+iy1, z2=x2+iy2, то из этого определения легко получить z:

z=z1-z2=(x1-x2)+i(y1-y2).                          (28.2)

Из равенства (28.2) следует, что геометрически комплексные числа вычитаются как векторы (см. рис. 165).

28.3 Умножение комплексных чисел

Произведением к омплексных чисел z1 =х1 +iy1 и z2=х2+iy2 называется комплексное число, определяемое равенством

z=z1 z2 =(x1 x2- у1 у2)+i(x1 y2+y1x 2 ).                    (28.3)

Отсюда, в частности, следует важнейшее соотношение

i 2 =- 1.                                                 

28.4. Деление комплексных чисел

Деление определяется как действие, обратное умножению. Частным двух комплексных чисел z1 и z2≠0 называется комплексное число z, которое, будучи умноженным на z2, дает число z1, т. е. z1/z2=z, если z2z=z1.

Если положить z1=x1+iy1; z2=х2+iy2≠0, z=х+iy, то из равенства (х2+iy2)(x+iy)=x1+iy1 следует

Решая систему, найдем значения х и у:

Таким образом,

2. Тригонометрическая форма записи комплексного числа.

Абсцисса a и ордината b комплексного числаa + b·i выражаются через модуль r и аргумент φформулами:

1.	a= r·cos(φ)
2.	b= r·sin(φ)

Поэтому всякое комплексное число можно представить в виде:

3.	a+b·i= r·(cos(φ)+ i·sin(φ))

Это так называемая нормальная тригонометрическая форма, или просто тригонометрическая форма комплексного числа.

В противоположность тригонометрической форме выражение видa + b·i называется алгебраической или координатной формой комплексного числа.

3. Степень с целым показателем. Основные свойства.

Выражение an (степень с целым показателем) будет определено во всех случаях, за исключением случая, когда a = 0 и при этом n меньше либо равно нулю. 

Свойства степеней

Основные свойства степеней с целым показателем:

am *an = a(m+n);

am : an = a(m-n) ( при a не равном нулю);

(am)n = a(m*n);

(a*b)n = an *bn;

(a/b)n = (an)/(bn) (при b не равном нулю);

a1 = a;

a0 = 1 ( при a не равном нулю);

Эти свойства будут справедливы для любых чисел a, b и любых целых чисел m и n. Стоит отметить также следующее свойство:

Если m>n, то am > an, при a>1 и am

4. Основные сведения о логарифмах. Основные свойства и соотношения.

Логарифмом числа   по основанию   (   ) называется такое число  , что  , то есть записи  и   равносильны. Логарифм имеет смысл, если  .

Если немного перефразировать - Логарифм числа   по основанию   определяется как показатель степени, в которую надо возвести число  , чтобы получить число   (Логарифм существует только у положительных чисел).

Логарифм в переводе с греческого буквально означает "число, изменяющее отношение".

Специальные обозначения:

Натуральный логарифм   - логарифм по основанию  , где   - число Эйлера.

Десятичный логарифм   - логарифм по основанию 10.

Свойства логарифмов:

1°      - основное логарифмическое тождество.

2°    

3°    

Логарифм единицы по любому положительному, отличному от 1, основанию равен нулю. Это возможно потому, что из любого действительного числа можно получить 1 только возведя его в нулевую степень.

4°      - логарифм произведения.

Логарифм произведения равен сумме логарифмов сомножителей.

5°      - логарифм частного.

Логарифм частного (дроби) равен разности логарифмов сомножителей.

6°      - логарифм степени.

Логарифм степени равен произведению показателя степени на логарифм ее основания.

7°    

8°    

9°      - переход к новому основанию.

5. Правила комбинаторики. Выборки элементов.

Большинство комбинаторных задач решается с помощью двух основных правил - правила суммы и правила произведения.

Правило суммы. Если некоторый объект   можно выбрать   способами, а другой объект   можно выбрать   способами, то выбор "либо  , либо  " можно осуществить   способами.

Правило произведения. Если объект   можно выбрать   способами, а после каждого такого выбора другой объект   можно выбрать (независимо от выбора объекта   способами, то пары объектов   и   можно выбрать   способами.

Размещениями из   элементов по   называются такие выборки, которые, имея по   элементов, выбранных из числа данных   элементов, отличаются одна от другой либо составом элементов, либо порядком их расположения.

Число размещений из   элементов по   обозначим   Используя основное правило комбинаторики, получаем:

Если  , то   - число таких размещений, которые отличаются только порядком расположения элементов. Такие размещения называются перестановками. Их число   находится по формуле

Выборки из   элементов, взятых из данных  , отличающихся только составом элементов, называются сочетаниями из   элементов по  . Число   таких сочетаний находится

6. Бином Ньютона. Свойства биномиальных коэффициентов.

Бином Ньютона. Это формула, представляющая выражение ( a + b ) n  при положительном целом  n  в виде многочлена:

            

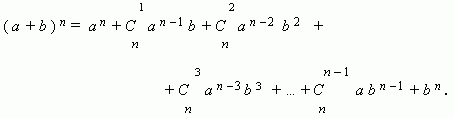
Заметим, что сумма показателей степеней для  a  и  b  постоянна и равна n.

7. Тригонометрические функции острого угла. Радианная мера угла, знаки тригонометрических функций. Значения тригонометрических функций.

Тригонометрические функции острого угла есть отношения различных пар сторон прямоугольного треугольника   ( рис.2 ):

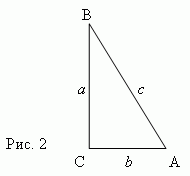
1) Синус - отношение противолежащего катета к гипотенузе:  sin A = a / c .  

2) Косинус - отношение прилежащего катета к гипотенузе:  cos A = b / c .

3) Тангенс - отношение противолежащего катета к прилежащему:  tan A = a / b .

4) Котангенс - отношение прилежащего катета к противолежащему: cot A = b / a .

Знак тригонометрической функции зависит исключительно от координатной четверти, в которой располагается числовой аргумент.

Все эти определения знакомы вам из курса алгебры старших классов. Однако нас интересуют не сами определения, а следствия, которые возникают на тригонометрической окружности. Взгляните:

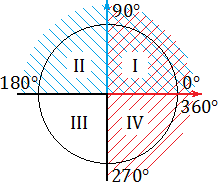
Синим цветом обозначено положительное направление оси OY (ось ординат), красным — положительное направление оси OX (ось абсцисс). На этом «радаре» знаки тригонометрических функций становятся очевидными. В частности:

sin α > 0, если угол α лежит в I или II координатной четверти. Это происходит из-за того, что по определению синус — это ордината (координата y ). А координата y будет положительной именно в I и II координатных четвертях;

cos α > 0, если угол α лежит в I или IV координатной четверти. Потому что только там координата x (она же — абсцисса) будет больше нуля;

tg α > 0, если угол α лежит в I или III координатной четверти. Это следует из определения: ведь tg α = y : x , поэтому он положителен лишь там, где знаки x и y совпадают. Это происходит в Iкоординатной четверти (здесь x > 0, y > 0) и III координатной четверти ( x < 0, y < 0).

Центральный угол, опирающийся на дугу, длина которой равна радиусу окружности, называется углом в 1 радиан.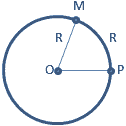

Градусная мера угла в 1 радиан равна:

Так как дуга длиной πR (полуокружность), стягивает центральный угол в 180°, то дуга длиной R, стягивает угол в π раз меньший, т.е.

И наоборот

Так как π = 3,14, то 1 рад = 57,3°

Если угол содержит a радиан, то его градусная мера равна

И наоборот

Обычно при обозначении меры угла в радианах наименование «рад» опускают.

Например, 360° = 2π рад, пишут 360° = 2π

В таблице указаны наиболее часто встречающиеся углы в градусной и радианной мере.

Градусы	0	15	30	45	60	75	90	120	135	150	180	270	360
Радианы	0	π/12	π/6	π/4	π/3	5π/12	π/2	2π/3	3π/4	5π/6	π	3π/2	2π

8. Решение простейших тригонометрических уравнений.

Уравнение, содержащее неизвестное под знаком тригонометрической функции, называется тригонометрическим.  

Простейшие тригонометрические уравнения. 

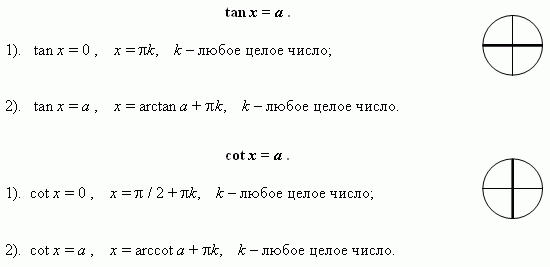
9. Решение тригонометрических неравенств.

Основной способ решения тригонометрических неравенств состоит в их сведении к неравенствам вида

sinx Ъ a,     cosx Ъ a,     tgx Ъ a,     ctgx Ъ a,

(1)

где a О R, символ "Ъ" означает знак сравнения и заменяет любой из знаков ">",   " ≥ ",   "<",  " ≤" и использовании следующих утверждений.

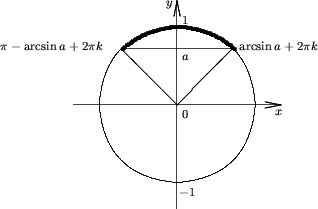
Утверждение 1. Множество решений неравенства

sinx > a

(2)

есть

R, если a < -1;

(arcsina + 2pk; p - arcsina + 2pk), если -1 ≤ a < 1;

Пустое множество, если a ≥ 1.

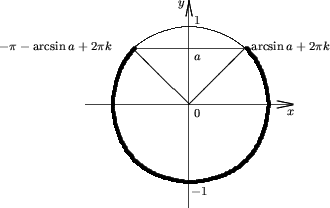
Утверждение 2. Множество решений неравенства

sinx < a

(3)

есть

R, если a > 1;

(-p - arcsina + 2pk; arcsina + 2pk), если -1 < a ≤ 1;

Пустое множество, если a ≤ -1.

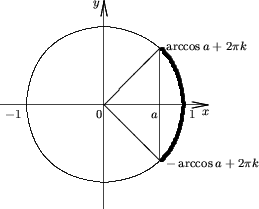
Утверждение 3. Множество решений неравенства

cosx > a

(4)

есть

R, если a < -1;

(2pk - arccosa; 2pk + arccosa), если -1 ≤ a < 1;

Пустое множество, если a ≥ 1.

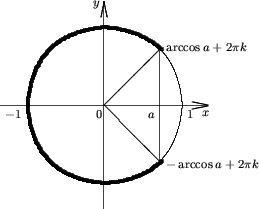
Утверждение 4. Множество решений неравенства

cosx < av

(5)

есть

R, если a > 1;

(2pk + arccosa; 2p(k + 1) - arccosa), если -1 < a ≤ 1;

Пустое множество, если a ≤ -1.

Утверждение 5. Множество решений неравенства

tgx > a

(6)

есть 

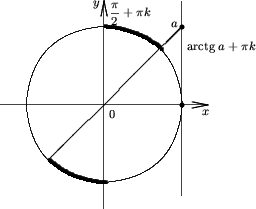
Утверждение 6. Множество решений неравенства

tgx < a

(7)

есть 

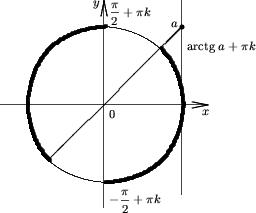
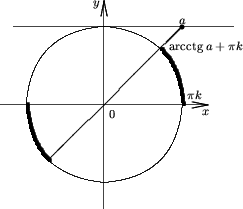
Утверждение 7. Множество решений неравенства

ctgx > a

(8)

есть  (pk; arcctga + pk).

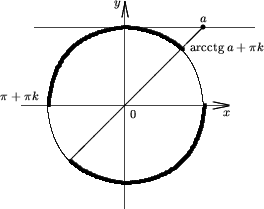
Утверждение 8. Множество решений неравенства

ctgx < a

(9)

есть  (arcctga + pk; p(k + 1))

Замечания. 1. Если знак неравенства (2)-(9) нестрогий, то во множестве решений неравенства включается также и множество решений соответствующего уравнения.

2. Утверждения 1-8 легко доказать используя графики и свойства соответствующих тригонометрических функций.

10. Понятие функции одной переменной. Способы задания функции одной переменной. Классификация функций одной переменной. Свойства функций.

Рассмотрим два числовых множества X и Y. Правило f, по которому каждому числу хI Х ставится в соответствие единственное число yI Y, называется числовой функцией, заданной на множестве Х и принимающей значения во множестве Y.

Таким образом, задать функцию, значит задать три объекта:

1) множество Х (область определения функции);

2) множество Y (область значений функции);

3) правило соответствия f (сама функция).

Например, поставим в соответствие каждому числу его куб. Математически это можно записать формулой y=x3. В этом случае правило f есть возведение числа х в третью степень. В общем случае, если каждому х по правилу f соответствует единственный y, пишут y = f(x). Здесь "х" называют независимой переменной или аргументом, а "y" -зависимой переменной (т.к. выражение типа x3 само по себе не имеет определенного числового значения пока не указано значение х) или функцией от х. О величинах х и y говорят, что они связаны функциональной зависимостью. Зная все значения х и правило f можно найти все значения у. Например, если х=2, то функция f(x) =x3принимает значение у= f(2) =23 =8.

Существуют несколько способов задания функции.

Аналитический способ. Функция f задается в виде формулы y=f(x). Например, y=3cos(x)+2x2. Этот способ является преобладающим в математических исследованиях и подробно рассматривается в классическом курсе математики. В географических исследованиях соответствие между переменными величинами x и y не всегда удается записать в виде формулы. Во многих случаях формула бывает неизвестна. Тогда для выражения функциональной зависимости используются другие способы.

 

Графический способ. На метеорологических станциях можно наблюдать работу приборов-самописцев, регистрирующих величины атмосферного давления, температуры воздуха, его влажности в любой момент времени суток. По полученному графику можно определить значения указанных величин в любой момент времени. Графиком функции y=f(x) называется множество всех точек плоскости с координатами (x, f(x)). График содержит всю информацию о функции. Имея перед собой график, мы как бы "видим функцию".

 

Табличный способ. Этот способ является наиболее простым. В одной строке таблицы записываются все значения аргумента (числа), а в другой – значения f(x), соответствующие каждому х. Например, зависимость температуры воздуха (Т) от времени суток (t) в определенный день можно представить таблицей.

 

t	0	1	2	3	4	5	6	7	8	9	10	11
T,0С	12	11	10	9	8	7	8	10	12	14	16	17

11. Линейная функция и её график. Свойства функции. Понятие обратной функции.

Линейная функция – это функция, которую можно задать формулой

y=kx+m, где x – независимая переменная, k и m – некоторые числа.

Применяя эту формулу, зная конкретное значение x, можно вычислить соответствующее значение y.

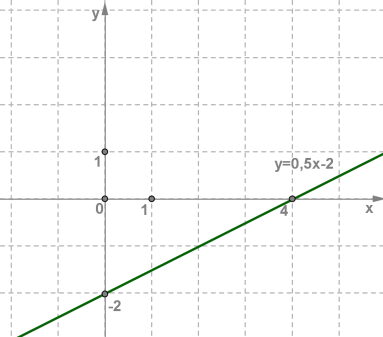
Пусть y=0,5x−2.

Тогда:

если  x=0, то y=−2;

если  x=2, то y=−1;

если  x=4, то y=0 и т.д. 

Обычно эти результаты оформляют в виде таблицы:

x	0	2	4
y	−2	−1	0

x - независимая переменная (или аргумент),

y - зависимая переменная.

Графиком линейной функции y=kx+m является прямая.

Чтобы построить график данной функции, нам нужны координаты двух точек, принадлежащих графику функции.

 

Построим на координатной плоскости xOy точки (0;−2) и (4;0) и

проведём через них прямую.

 

Свойства линейной функции  .

1. Область определения функции – множество всех действительных чисел.

2. Область изменения функции при условии, что   – множество всех действительных чисел. Если  , то множество значений функции состоит из одной точки  .

3. При  ,   функция не является ни четной, ни нечетной. Если   (  любое) – функция четная. Если   ( любое) функция нечетная.

4. При   функция возрастает при любых  . При   функция убывает при любых  . При   функция постоянна.

Функция, которая, принимает каждое свое значение в единственной точке своей области определения, называется обратимой функцией. Например, линейная функция будет являться обратимой функцией. А квадратичная функция или функция синус не будет являться обратимыми функциями. Так как одно и то же значение функция может принимать при различных аргументах.

Положим, что f есть некоторая произвольная обратимая функция. Каждому числу из области её значений y0, соответствует лишь одно число из области определения x0, такое что f(x0) = y0.

Если теперь мы каждому значению х0 поставим в соответствие значение y0, то получим уже новую функцию. Например, для линейной функции f(x) = k * x + b функция g(x) = (x - b)/k будет являться обратной.

Если некоторая функция g в каждой точке х области значений обратимой функции f принимает значение у такое, что f(y) = x, то говорят, что функция g – есть обратная функция к f.

Если у нас будет задан график некоторой обратимой функции f, то для того чтобы построить график обратной функции, можно пользоваться следующим утверждением: график функции f и обратной к ней функции g будут симметричны относительно прямой, заданной уравнением y = x.

Если функция g является обратной к функции f, то функция g будет являться обратимой функцией. А функция f будет обратной к функции g. Обычно говорят, что две функции f и g взаимно обратные друг к другу.

На следующем рисунке представлены графики функций f и g взаимно обратных друг к другу.

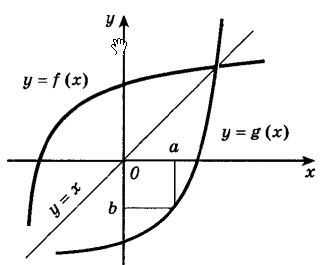
Выведем следующую теорему: если функция f возрастает (или убывает) на некотором промежутке A, то она обратима. Обратная к а функция g, определенная в области значений функции f, также является возрастающей (или соответственно убывающей) функцией. Данная теорема называется теоремой об обратной функции.