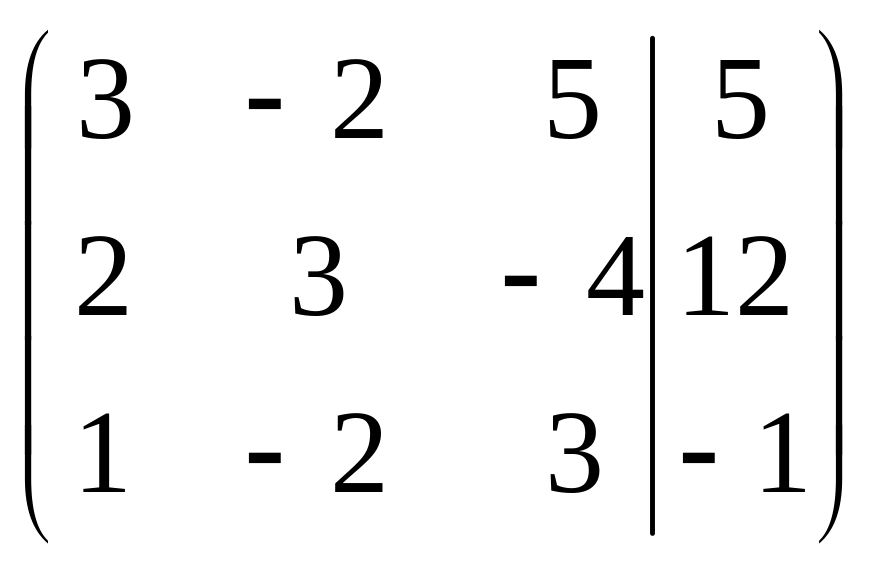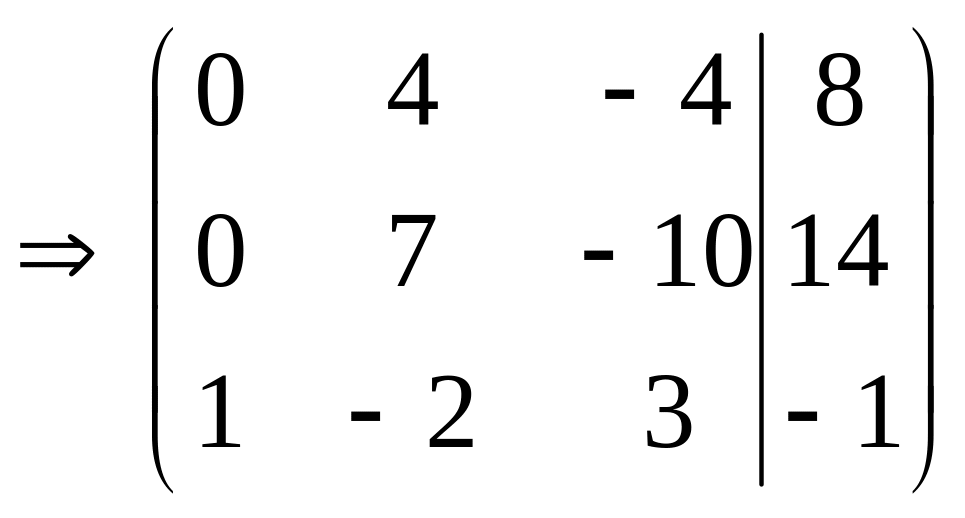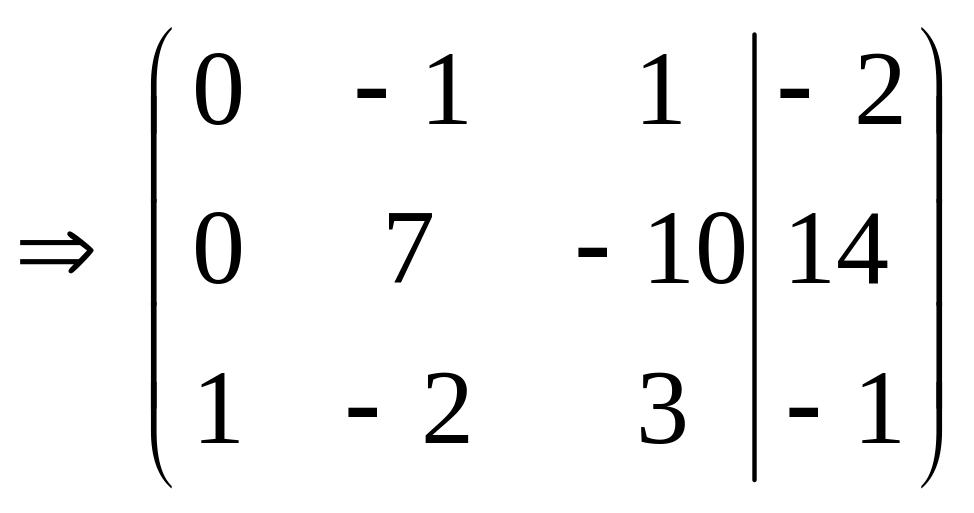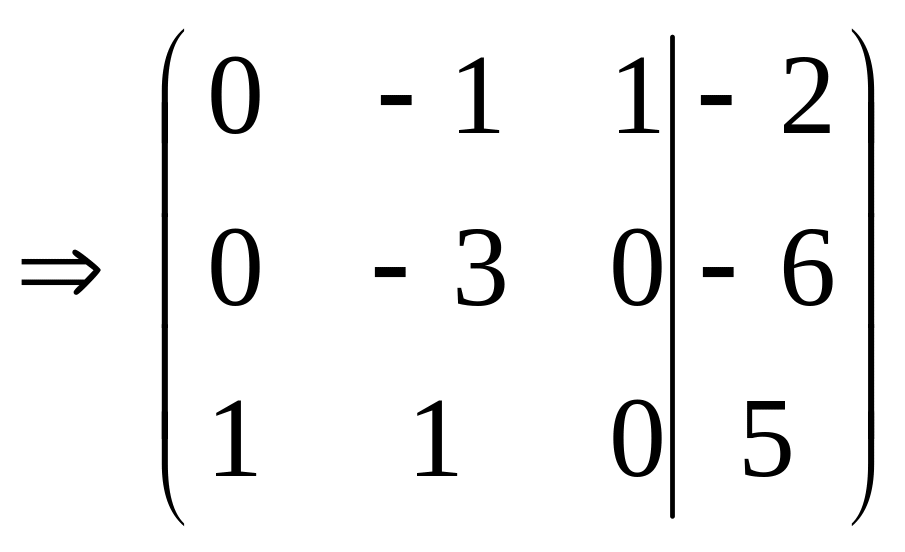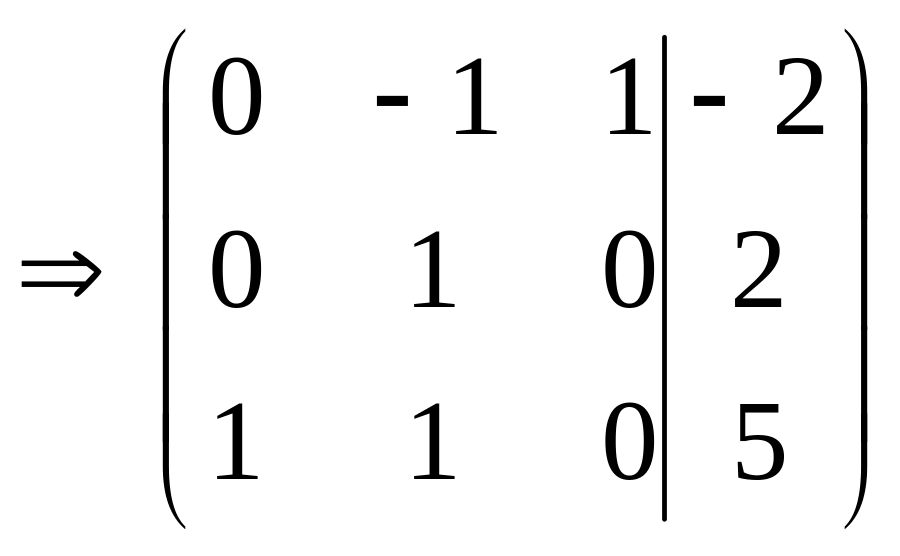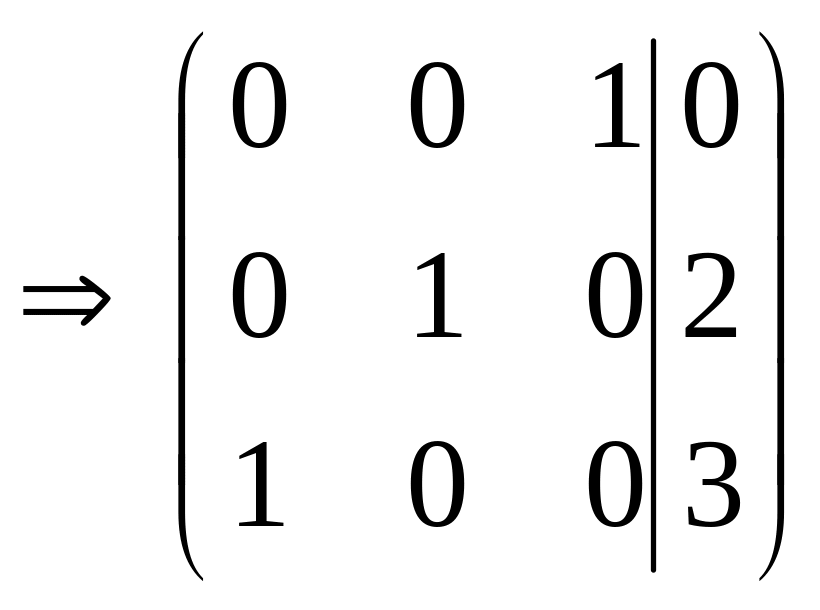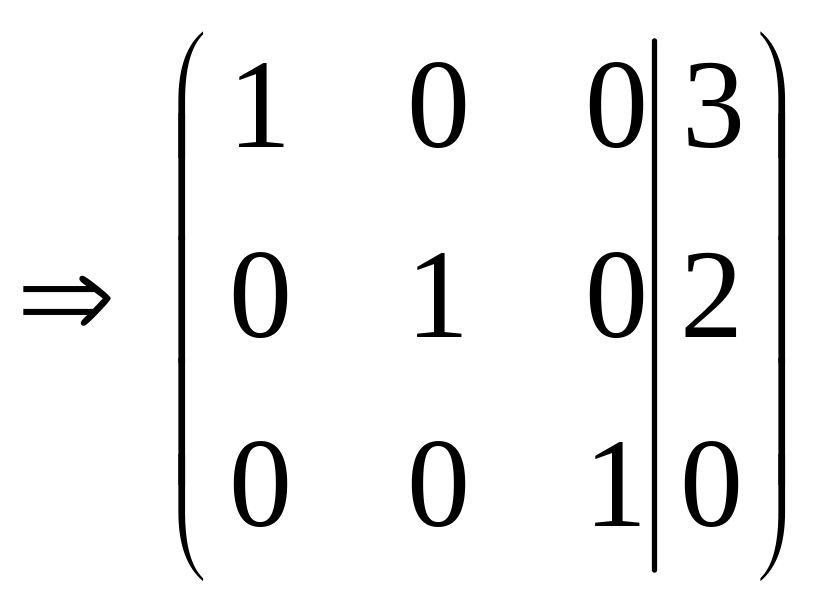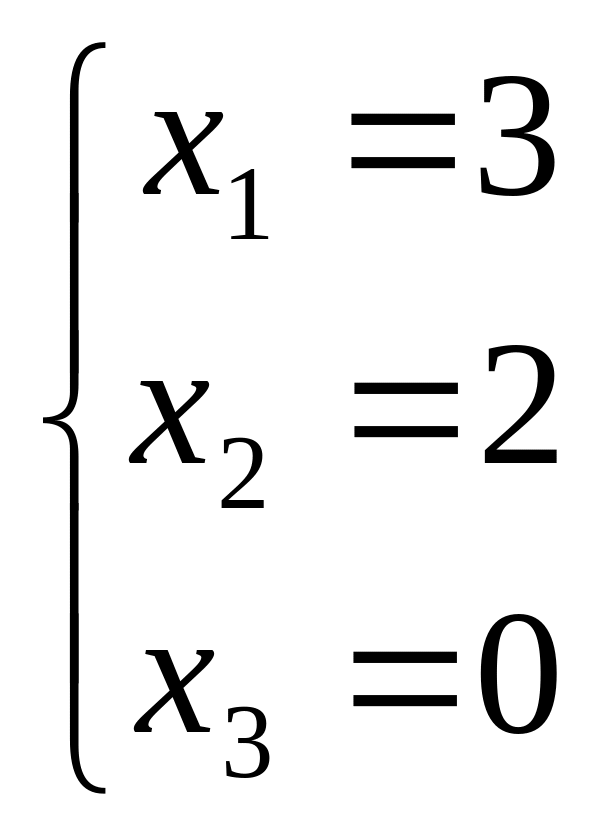32

2. Практическое задание.

Решить систему линейных алгебраических уравнений:

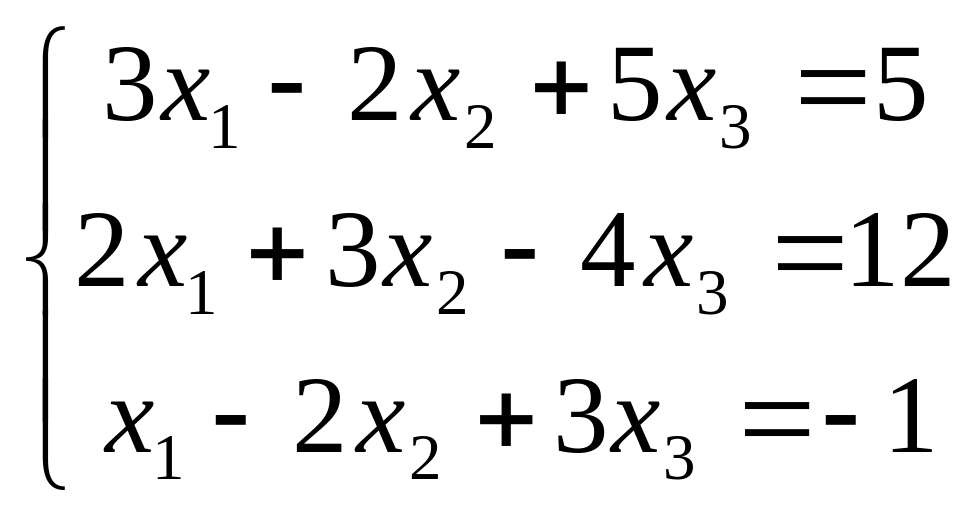
1. По формулам Крамера.

2. Методом Гаусса.

3. Методом квадратных корней.

4. Методом обратных матриц.

5. Методом релаксаций.

Решение:

1. Решение слау по формулам Крамера.

Обозначим :

, , ,

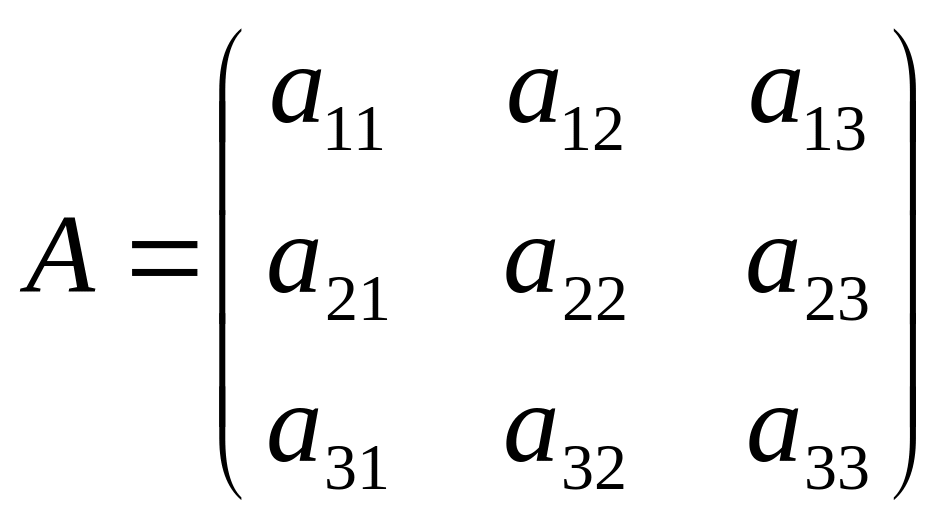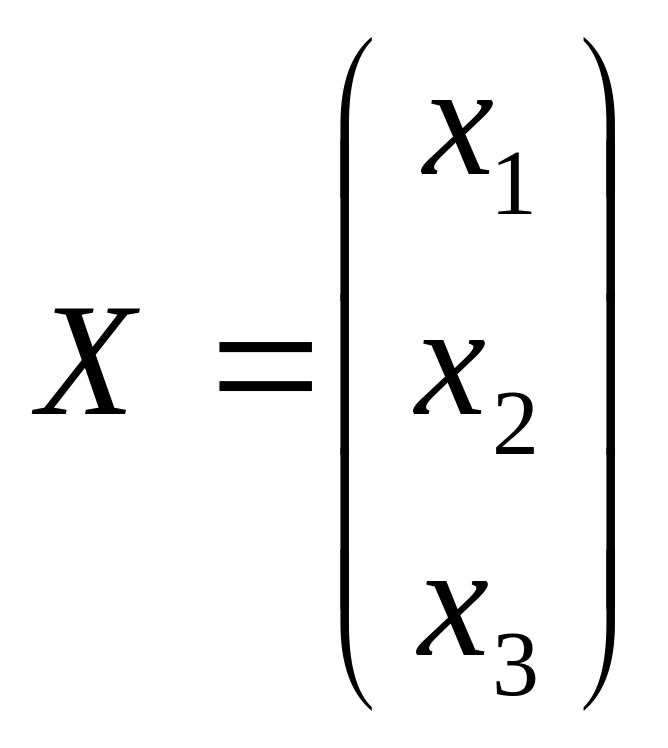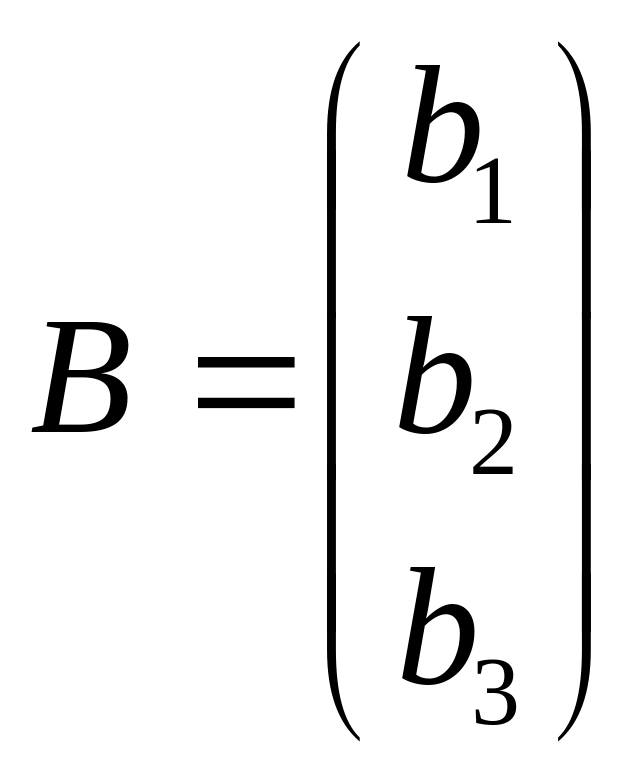Систему уравнений можно представить в виде: А ∙ X = В

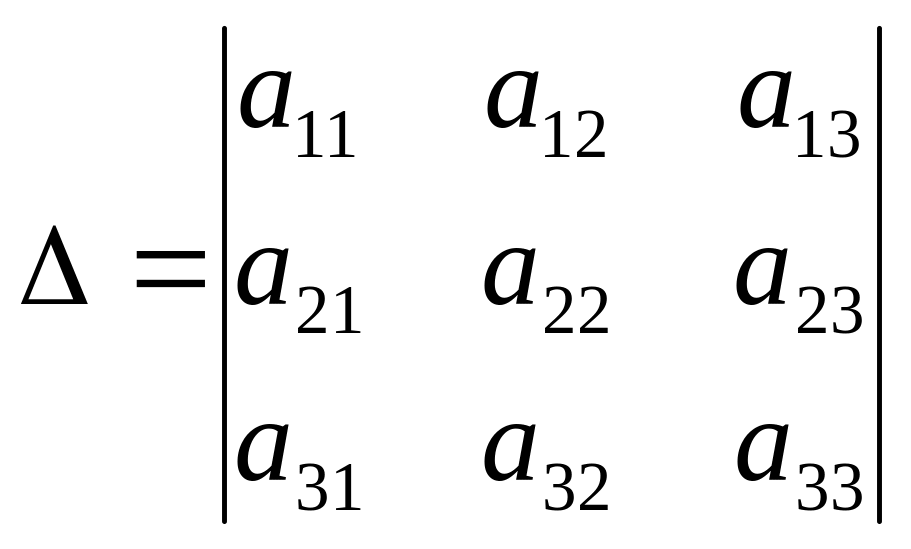– определитель системы.

, , .

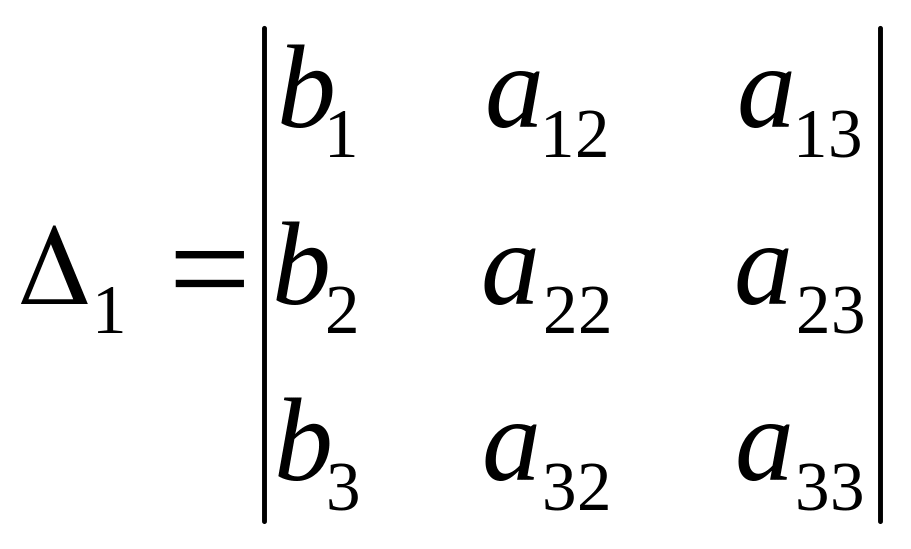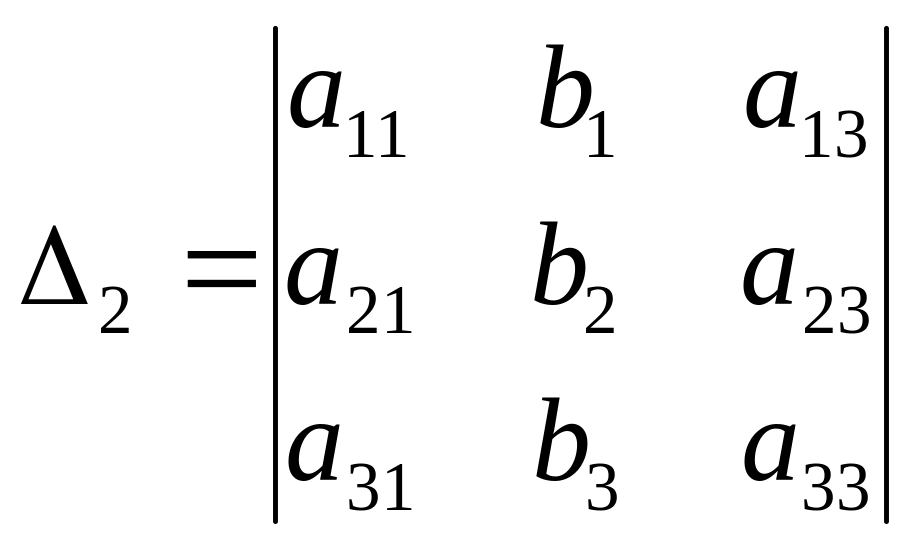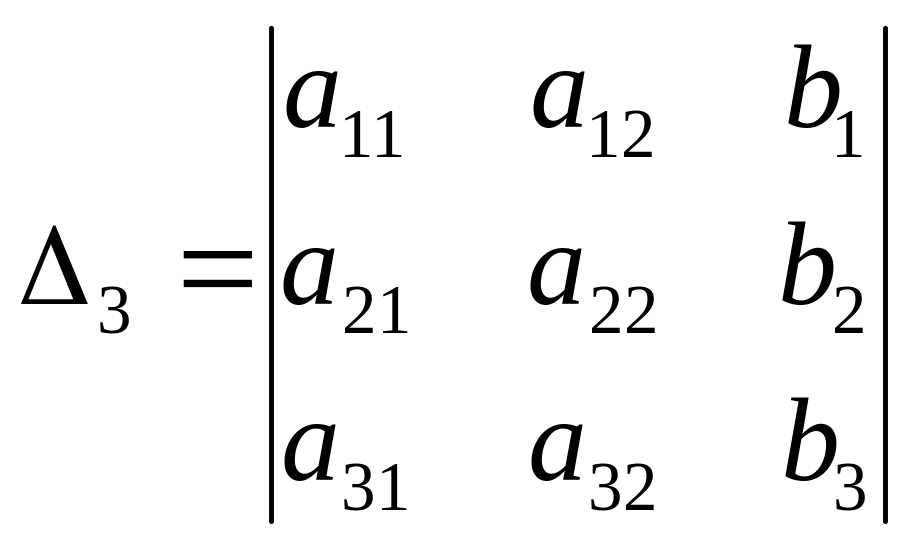, , – формулы Крамера.

Имеем:

, , .

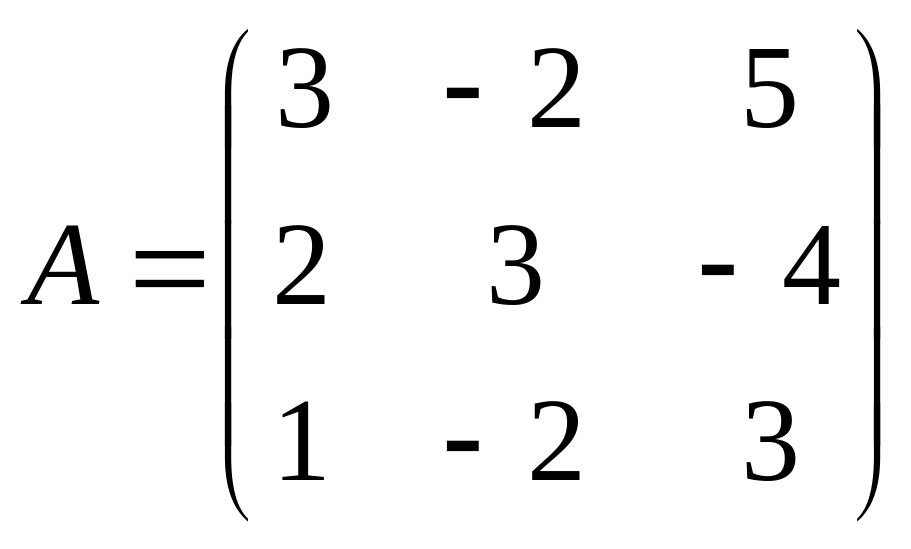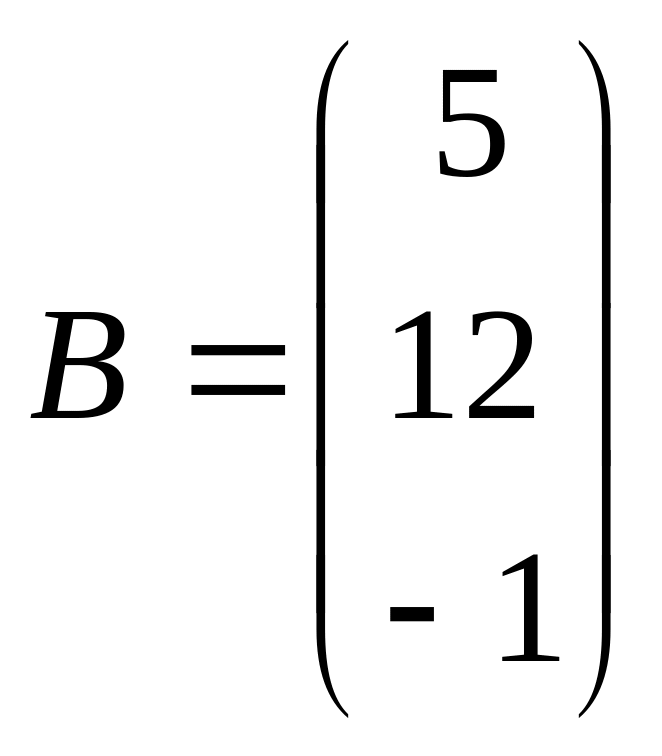Так как матрица А квадратная, имеет размер 3*3, то метод Крамера применим.

Вычислим определитель системы (по первой строке):

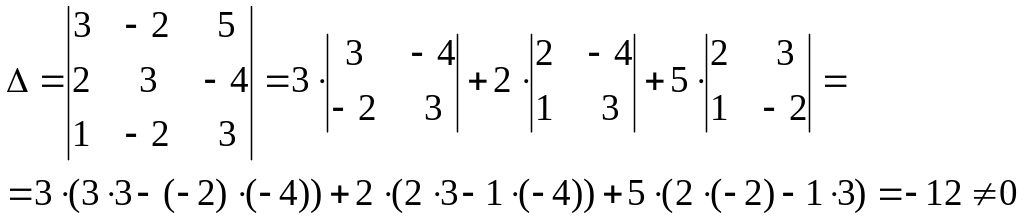
Следовательно, система является совместной и определенной.

Имеет единственное решение.

Найдем соответствующие определители , и , заменяя поочередно первый, второй и третий столбец столбцом свободных членов.

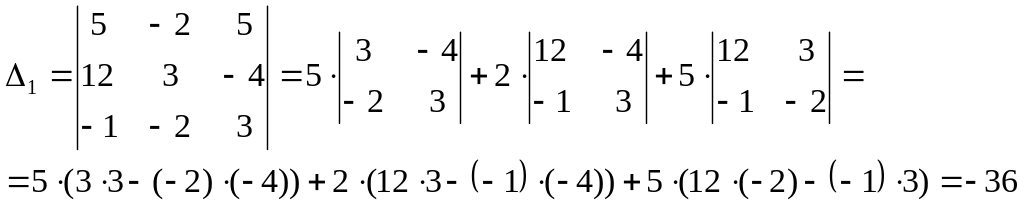
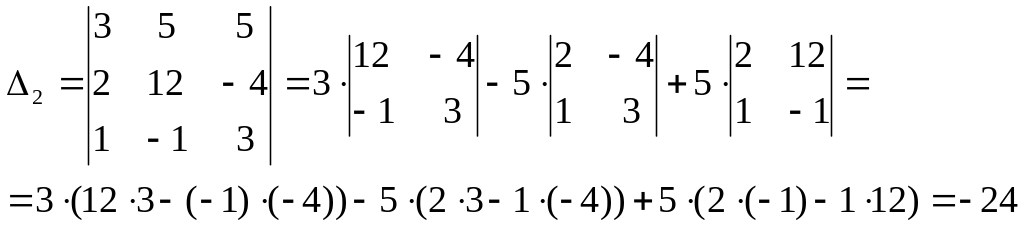
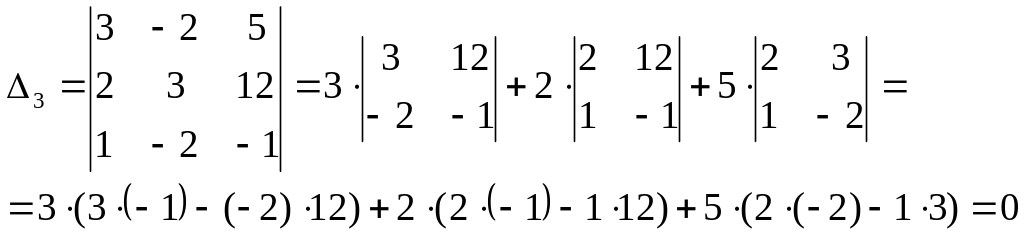
По формулам Крамера, получаем:

, , .

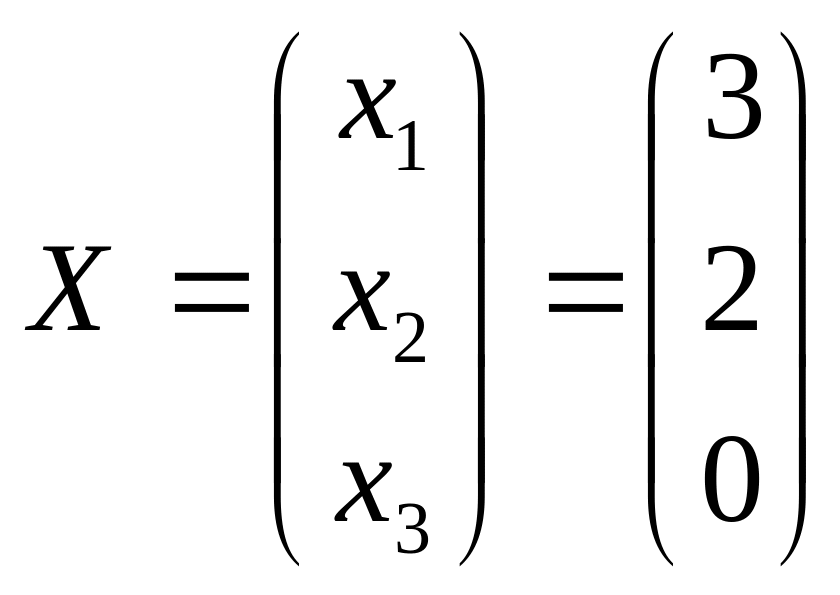
Итак, получили: x₁ = 3 , х₂ = 2 , х₃ = 0 – решение системы уравнений.

2.2. Решение слау методом Гаусса.

Запишем расширенную матрицу системы и проведем с ней элементарные преобразования, приведя ее к ступенчатому виду.

		Третью строку умножим на (-3) и прибавим к первой.
		Третью строку умножим на (-2) и прибавим ко второй.
		Первую строку разделим на (-4).
		Первую строку умножим на 10 и сложим со второй.
		Первую строку умножим на (-3) и прибавим к третьей.
		Вторую строку разделим на (-3).
		Вторую строку прибавим к первой.
		Вторую строку умножим на (-1) и прибавим к третьей.
		Поменяем первую и третью строки местами.

Тогда система уравнений примет вид:

Получили x₁ = 3 , х₂ = 2 , х₃ = 0 – решение системы уравнений.