
- •Визначення в’язкості рідини методом Стокса
- •Теоретичні відомості
- •Методика вимірювання та опис установки
- •Контрольні питання
- •Визначення відношення питомих теплоємностей повітря при постійному тиску і постійному об’ємі
- •Опис лабораторної установки і методика вимірювання
- •Послідовність виконання роботи
- •Контрольні питання
- •Вимірювання теплоємності металів методом охолодження
- •Теоретичні відомості
- •Питома теплоємність пов’язана з молярною співвідношенням
- •Методика вимірювань та опис установки
- •Згідно з формулою ( 12 ) для еталонного зразка маємо
- •Потім побудувати графік залежності
- •Послідовність виконання завдання № 2 Визначення молярної теплоємності металів і перевірка закону Дюлонга–Пті
- •Контрольні питання
- •Визначення коефіцієнта тепловіддачі поверхні пластини в умовах природної та вимушеної конвекції
- •Теоретичні відомості
- •Методика вимірювання та опис установки
- •Контрольні питання
- •Вивчення роботи компресорного холодильника і визначення його характеристик
- •Теоретичні відомості
- •Методика вимірювання та опис установки
- •Порядок виконування роботи
- •Контрольні питання
- •Визначення характеристик холодильної машини та теплового насоса
- •Теоретичні відомості
- •Опис лабораторної установки і методика вимірювання
- •Контрольні питання
- •Вимірювання питомої теплоти згорання газоподібного та рідкого палива
- •Теоретичні відомості
- •Опис лабораторної установки і методика вимірювання
- •Контрольні питання
- •Вимірювання абсолютної вологості повітря конденсаційним гігрометром та перевірка рівняння стану ідеального газу на прикладі водяної пари
- •Теоретичні відомості
- •Конструкція експериментальної установки
- •Послідовність виконання лабораторної роботи
- •Контрольні питання
- •Лабораторна робота № 107. Визначення прискорення вільного падіння тіл за допомогою маятника. . . . .59
Контрольні питання
1. Що таке в’язкість рідини?
2. Записати формулу Ньютона для внутрішнього тертя.
3. Який фізичний зміст має коефіцієнт динамічної в’язкості?
4. Як пов’язані між собою коефіцієнти динамічної і кінематичної в’язкості?
В яких одиницях вони виміряються?
5. Чому при підвищенні температури в’язкість рідин зменшується? Як це впливає на роботу механізмів?
6. В чому полягає сутність методу Стокса вимірювання в’язкості рідини? Запишіть формулу Стокса.
7. Чому при визначенні коефіцієнта в’язкості потрібно враховувати наявність стінок посудини?
8. Як впливає в’язкість води на гідродинамічний опір судна?
Лабораторна робота № 109
Визначення відношення питомих теплоємностей повітря при постійному тиску і постійному об’ємі
Мета роботи:
Вивчити термодинамічні процеси в балоні з повітрям.
Визначити відношення теплоємностей повітря
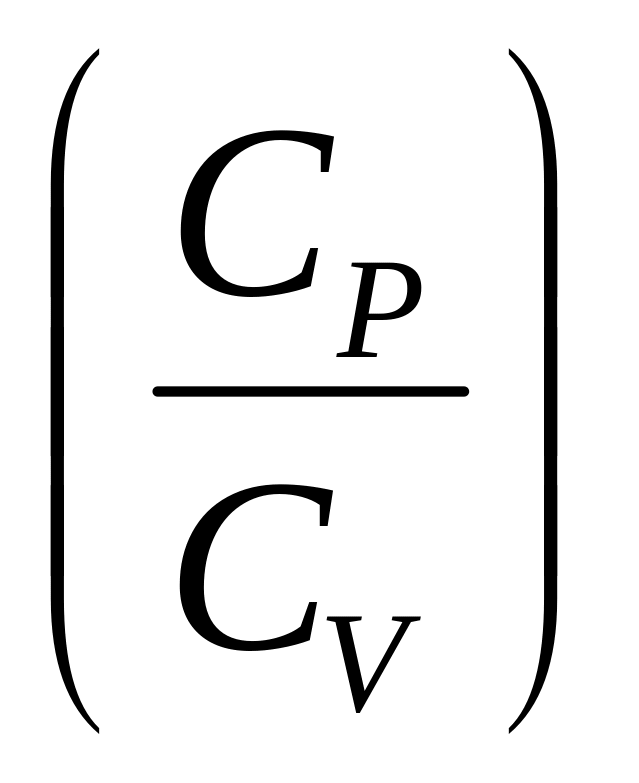 .
.За результатами експерименту розрахувати коефіцієнт тепловіддачі з поверхні експериментального об’єму.
Прилади і матеріали: балон з розподільчими кранами; рідинний U-подібний манометр; насос ручний; секундомір.
Опис лабораторної установки і методика вимірювання
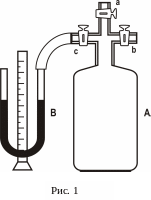 Установка
(рис.1) складається зі скляного балона
А, з’єднаного трубкою з рідинним
манометром В. Краном а балон А
з’єднується з зовнішнім повітрям. Через
кран в у балон нагнітається повітря
ручним насосом. Кран с служить для
з’єднання балону з манометром В.
Установка
(рис.1) складається зі скляного балона
А, з’єднаного трубкою з рідинним
манометром В. Краном а балон А
з’єднується з зовнішнім повітрям. Через
кран в у балон нагнітається повітря
ручним насосом. Кран с служить для
з’єднання балону з манометром В.
Для
визначення відношення теплоємностей
![]() повітря, що знаходиться в балоні, з ним
проводять послідовність термодинамічних
процесів, представлених на рV-діаграмі,
рис.2.
повітря, що знаходиться в балоні, з ним
проводять послідовність термодинамічних
процесів, представлених на рV-діаграмі,
рис.2.
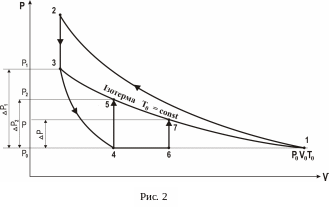
Позначимо через Р0 , V0 , T0 вихідні величини термодинамічних параметрів газу в балоні. Спочатку в балон накачується повітря (процес 12 ). При цьому газ в балоні стискається і нагрівається. Потрібен деякий час на вирівнювання температури повітря всередині балону з температурою оточуючого середовища. Після ізохоричного охолодження до початкової кімнатної температури Т0 (процес 23) газ має деякий тиск Р1, а на манометрі встановиться певна різниця висот рівнів h1.
Потім краном а з’єднують балон з атмосферою і газ адіабатично розширюється (процес 34). Газ при цьому охолоджується, його тиск падає до величини атмосферного Р0 , а температура – до величини Т1 Т0.
В момент досягнення тиску Р0 кран а перекривається, і газ ізохорично нагрівається до кімнатної температури Т0 (процес 45). В кінцевому стані тиск газу Р2 Р0, а на манометрі встановиться різниця висот рівнів рідини h2 h1.
Маса газу, що знаходиться в балоні, в початковому стані виражається співвідношенням
![]() (1)
(1)
Протягом всіх термодинамічних процесів маса газу в балоні більше або дорівнює m0. Назвемо масу m0 робочою масою газу. Ця маса повинна весь час залишатися в балоні. Газ, що накачується і випускається з балону, служить лише для стискання і розширення робочої маси газу m0.
Введемо позначення Р1 = Р1 – Р0 і Р2 = Р2 – Р0. Оскільки перехід з 3-го в 4-й стан здійснюється адіабатично, то можна записати:
![]() (2)
(2)
Перехід з 4-го стану в 5-й здійснюється ізохорично, отже:
![]() (3)
(3)
Виключивши
з рівнянь (2) і (3) температуру Т1
і скоротивши потім на
![]() ,
отримаємо
,
отримаємо
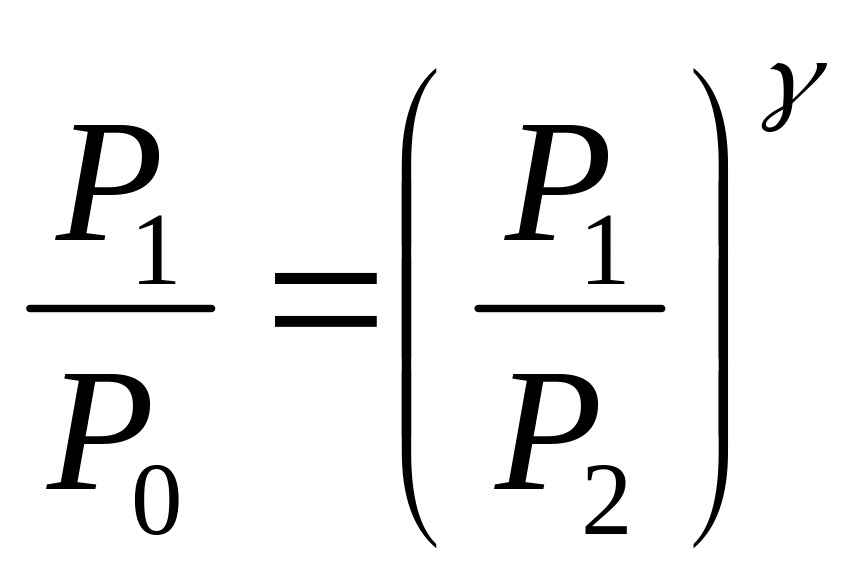 або
або
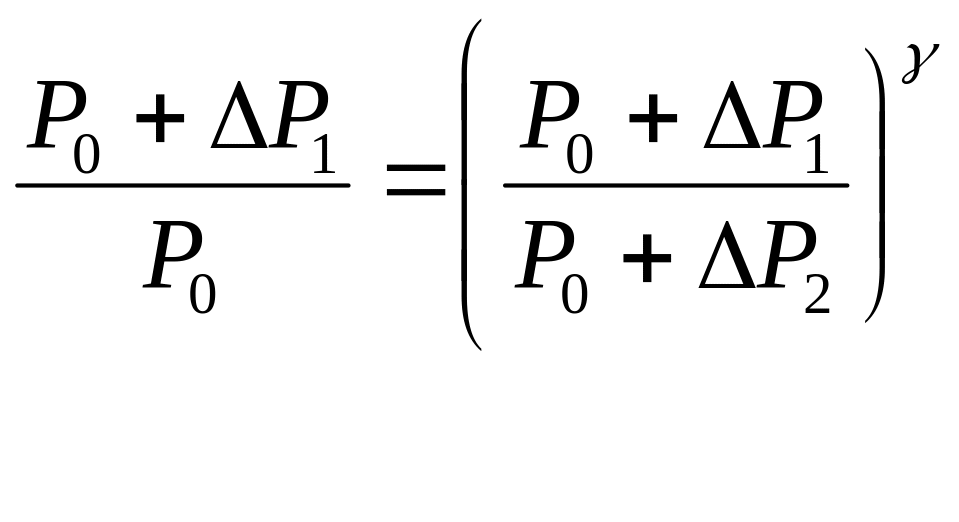 (4)
(4)
Розв’яжемо рівняння (4) відносно показника адіабати:
![]() .
(5)
.
(5)
У
роботі завжди виконується умова
![]() P1,
P2
<< P0
, що еквівалентно умові
P1/P0,
P2/
P0
<< 1.
Остання умова дозволяє з точністю до
членів другого порядку малості (
P1/P0)2
замінити
у (5) логарифми – першими членами їх
розкладу у ряди Тейлора, тобто відповідно:
P1,
P2
<< P0
, що еквівалентно умові
P1/P0,
P2/
P0
<< 1.
Остання умова дозволяє з точністю до
членів другого порядку малості (
P1/P0)2
замінити
у (5) логарифми – першими членами їх
розкладу у ряди Тейлора, тобто відповідно:
ln(
1 +
P1/P0)
![]() P1/P0;
ln(
1 +
P2/P0)
P2/P0
.
P1/P0;
ln(
1 +
P2/P0)
P2/P0
.
Таким чином, отримаємо:
![]() або
або
![]() (6)
(6)
Отже, при такому методі розрахунку необхідно виконання наступних умов:
1. В процесі 34 кран балону повинен бути перекритий в момент, коли тиск в балоні буде дорівнювати Р0.
2. Час, протягом якого тиск в балоні зменшується від Р1 до Р0 , повинен бути достатньо малим, так щоб теплообміном з оточуючим повітрям можна було знехтувати.
Розглянемо вплив часу t, протягом якого кран а ще залишається відкритим після досягнення тиску Р0, на результат дослідження.
Припустимо, що після досягнення тиску Р0 кран залишається відкритим ще деякий час t. За цей час відбувається ізобаричне нагрівання (процес 46) за рахунок теплообміну газу зі стінками балону, а також вихід частини газу з балону, викликаний нагріванням і розширенням цього газу. Величину t назвемо часом затримки.
Після того, як кран а закривається (точка 6), відбувається ізохоричне нагрівання (процес 67). Тиск в балоні досягає величини Р0 + Р. Кінцевий стан: точка (7) лежить на тій самій ізотермі, що і точки 1, 3 і 5, але Р Р1.
З цього розгляду видно, що Р залежить від часу затримки t. Таким чином, якщо прийняти до уваги теплообмін і вихід частки газу з балону за час t, то , розраховане за формулою (7), буде мати велику похибку.
Розглянемо детальніше процес охолодження протягом часу t. Рівняння балансу енергії для газу, що знаходиться в балоні, може бути записано у вигляді
- m сP d T = S (T – T0) d t, (10)
де сP – питома теплоємність газу; - коефіцієнт тепловіддачі з поверхні балону;
m – змінна
маса газу в балоні (![]() );
Т – температура газу в момент часу
t; S
– площа поверхні балону
з повітрям.
);
Т – температура газу в момент часу
t; S
– площа поверхні балону
з повітрям.
Розв’язуючи це рівняння, отримаємо вираз:
![]()
Константу інтегрування А знайдемо з умови: при t = 0 Т1 = Т0 - Т1. Кінцеве співвідношення буде мати вигляд:
![]() .
(11)
.
(11)
Температура газу Т тим більша, чим більший час витримки t. Після того, як в момент часу t кран а перекривається, нагрівання газу в балоні продовжується ізохорично. Тиск газу остаточно досягає величини
Р = Р0 + Р.
З умови ізохоричності виходить, що
![]() ,
(12)
,
(12)
Для малих Р1
і Т1
з рівняння адіабатичного процесу (34)
виходить співвідношення:
![]() (13)
(13)
Підставляючи співвідношення (12) і (13) в (11) і нехтуючи членами другого порядку малості, отримуємо формулу
![]() ,
(14)
,
(14)
Це відношення
враховує як теплообмін, так і вихід
частини газу з балону в процесі нагрівання.
Співвідношення (14) дозволяє знайти
за виміряними при різних величинах t
значеннями Р1
і Р.
Графік залежності
![]() від часу витримки t є лінійною
функцією. Якщо екстраполювати цей графік
до t = 0, то він буде відсікати на осі
ординат відрізок:
від часу витримки t є лінійною
функцією. Якщо екстраполювати цей графік
до t = 0, то він буде відсікати на осі
ординат відрізок:
![]() ,
(15)
,
(15)
З рівняння (15) легко знаходиться відношення теплоємностей
![]() ,
(16)
,
(16)
