Лабораторна робота № 108

Визначення в’язкості рідини методом Стокса

Мета роботи: Експериментально визначити в’язкість рідини

Теоретичні відомості

В’язкість рідини, як і внутрішнє тертя в газах, зумовлена передачею кількості руху від одного шару рідини до іншого, що рухаються з різними швидкостями. При цьому імпульс переноситься від шару з більшою швидкістю до шару з меншою швидкістю. У результаті швидкості різних шарів рідини прагнуть до вирівнювання. Отже, в’язкість - це властивість рідини чи газу вирівнювати швидкості руху різних шарів.

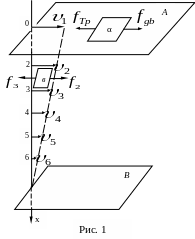
На рис.1 зображена одинична площадка α на поверхні А і показані прикладені до неї сили: зовнішня рушійна сила f_gb і сила внутрішнього тертя f_Тр . В результаті зрівноваження вказаних сил (f_gb = − f_gb ), коли поверхня А рухається рівномірно.

Аналогічна картина має місце і для будь-якої горизонтальної одиничної площадки між площинами А і В, наприклад, одинична площадка в, яка знаходиться між шарами 2 і 3 (рис.1).

Сила в’язкості визначається за формулою Ньютона:

, (1)

де - градієнт швидкості (вісь х обирається в напрямку найбільшої зміни швидкості υ); η – коефіцієнт динамічної в’язкості середовища; S – площа дотику.

Величина коефіцієнта динамічної в’язкості η має фізичний зміст сили, яка діє між двома шарами рідини з площею дотику S = 1м² при градієнті швидкості 1мс^-1:

. (2)

Коефіцієнт динамічної в’язкості пов’язаний з коефіцієнтом кінематичної в’язкості співвідношенням:

, (3)

де ν – коефіцієнт кінематичної в’язкості; ρ – густина рідини. У системі СІ динамічна в’язкість вимірюється в Па·с, кінематична – у м²/с.

В’язкість рідини залежить від температури, зменшуючись з її підвищенням. Це цілком природно, бо при цьому полегшується взаємне переміщення молекул. Для опису температурної залежності коефіцієнта η рідин широкого використання знайшла формула Френкеля:

, (4)

де А - сталий коефіцієнт; ΔЕ - енергія активації.

Співвідношення (4) підкреслює, що взаємне переміщення молекул рідини (їхня рухливість) пов’язане з послідовним подоланням енергетичного бар’єру при переході з одного рівноважного стану в інше.

Формула Френкеля досить точно описує залежність η(Т) не тільки простих, а й складних рідин. При зниженні температури дуже в’язка рідина перетворюється в аморфне тіло.

В 1883р. видатний російський вчений і інженер М.П.Петров у своїй роботі "Трение в машинах и влияние на него смазывающей жидкости" розрахував силу тертя, яка діє на змащений вал, що обертається у підшипнику:

, (5)

де S - поверхня валу; δ – товщина зазору; υ – швидкість руху поверхні валу.